hdu.1111.Secret Code(dfs + 秦九韶算法）

Secret Code

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 670    Accepted Submission(s): 109

Problem Description

The Sarcophagus itself is locked by a secret numerical code. When somebody wants to open it, he must know the code and set it exactly on the top of the Sarcophagus. A very intricate mechanism then opens the cover. If an incorrect code is entered, the tickets inside would catch fire immediately and they would have been lost forever. The code (consisting of up to 100 integers) was hidden in the Alexandrian Library but unfortunately, as you probably know, the library burned down completely. 
But an almost unknown archaeologist has obtained a copy of the code something during the 18th century. He was afraid that the code could get to the ``wrong people'' so he has encoded the numbers in a very special way. He took a random complex number B that was greater (in absolute value) than any of the encoded numbers. Then he counted the numbers as the digits of the system with basis B. That means the sequence of numbers an, an-1, ..., a1, a0 was encoded as the number X = a0 + a1B + a2B2 + ...+ anBn. 
Your goal is to decrypt the secret code, i.e. to express a given number X in the number system to the base B. In other words, given the numbers X and Byou are to determine the ``digit'' a0 through an. 

 

 

Input

The input consists of T test cases. The number of them (T) is given on the first line of the input file. Each test case consists of one single line containing four integer numbers Xr, Xi, Br, Bi (|Xr|,|Xi| <= 1000000, |Br|,|Bi| <= 16). These numbers indicate the real and complex components of numbers X and B, i.e. X = Xr + i.Xi, B = Br + i.Bi. B is the basis of the system (|B| > 1), X is the number you have to express. 

 

 

Output

Your program must output a single line for each test case. The line should contain the ``digits'' an, an-1, ..., a1, a0, separated by commas. The following conditions must be satisfied:  for all i in {0, 1, 2, ...n}: 0 <= ai < |B|  X = a0 + a1B + a2B2 + ...+ anBn  if n > 0 then an <> 0  n <= 100  If there are no numbers meeting these criteria, output the sentence "The code cannot be decrypted.". If there are more possibilities, print any of them. 

 

 

Sample Input

4 -935 2475 -11 -15 1 0 -3 -2 93 16 3 2 191 -192 11 -12

 

 

Sample Output

8,11,18 1 The code cannot be decrypted. 16,15

 

#include<stdio.h>
#include<string.h>
const int M = 5000000 ;
typedef __int64 ll ;
ll xr , xi , br , bi ;
int n ;
ll ini ;
ll a[M] ;
ll t ;

bool dfs (ll l , ll r , int dep)
{
    if (dep > 100) return false ;
    if (l == 0 && r == 0) {
        n = dep ;
        return true ;
    }
    ll al , ar ;
    for (int i = 0 ; i * i < ini ; i ++) {
        al = l - i ; ar = r ;
        if ( ( (1ll * al * br + 1ll *ar * bi) % t ) == 0 && ((1ll *ar * br -1ll * al * bi) % t) == 0 ) {
            a[dep] = i ;
            if ( dfs ( ((1ll * al * br + 1ll * ar * bi) / t) , ((1ll * ar * br - 1ll * al * bi) / t) , dep + 1) )
                return true ;
        }
    }
    return false ;
}

int main ()
{
    //freopen ("a.txt" , "r" , stdin ) ;
    ll T ;
    scanf ("%I64d" , &T ) ;
    while (T --) {
        scanf ("%I64d%I64d%I64d%I64d" , &xr , &xi , &br , &bi ) ;
        t = br * br + bi * bi ;
        ini = br * br + bi * bi ;
        if (dfs (xr  , xi , 0) ) {
             if (n == 0) puts ("0") ;
             else {
                for (int i = n - 1 ; i >= 0 ; i --) printf ("%I64d%c" , a[i] , i == 0 ? '\n' : ',') ;
             }
        }
        else puts ("The code cannot be decrypted.") ;
    }
    return 0 ;
}

秦九韶算法：

一般地，一元n次多项式的求值需要经过[n（n+1）]/2次乘法和n次加法，而秦九韶算法只需要n次乘法和n次加法。在人工计算时，一次大大简化了运算过程。

把一个n次多项式

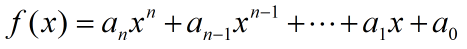
改写成如下形式：

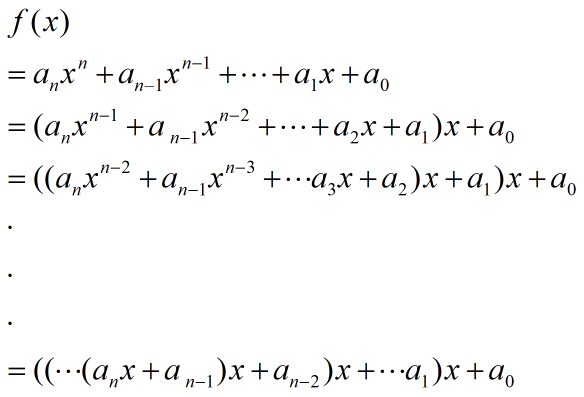
求多项式的值时，首先计算最内层括号内一次多项式的值，即

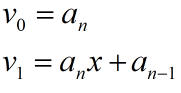
然后由内向外逐层计算一次多项式的值，即

这样，求n次多项式f(x)的值就转化为求n个一次多项式的值。

结论：对于一个n次多项式，至多做n次乘法和n次加法。（当最高次项系数不为1时分别为n次乘法和n次加法 ，当最高次项系数为1时，分别为n-1 次乘法 ，n次加法。）

复数除法运算：

设复数 a + bi  ,  c + di ;

t = c * c + d * d ;

则 (a + bi) / (c + di ) = (ac + bd) / t + （bc - ad) / t  * i ;