AVL树的java实现
AVL树之java实现
AVL树的介绍:
一、判断二叉排序树是否平衡
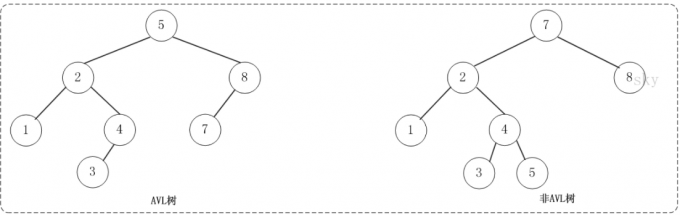
AVL树是高度平衡的二叉树,他的特点是:AVL树种任何节点的两个子树的高度差最大差别为1
二叉排序树平衡的充分必要条件是器每个节点的左右子树高度差的绝对值小于1.叶子节点的高度为1,其父节点的高度为2,依次增加,直到root节点,二叉排序树的高度就是root节点的高度。
上面的两张图片,左边的是AVL树,它的任何节点的两个子树的高度差都<=1,而右边的不是AVL树,因为根节点7的左右子树的高度相差为2(以2为根节点的子树的高度是3,而以8为根节点的树的高度是1).
二、AVL树的java实现
1.节点
1.1节点定义
//AVL树的节点(内部类)
class AVLTree01Node<T extends Comparable<T>>{
T value; //节点的值
int height; //高度
AVLTree01Node<T> left; //左孩子
AVLTree01Node<T> right; //右孩子
public AVLTree01Node(T value, AVLTree01Node<T> left, AVLTree01Node<T> right) {
this.value = value;
this.left = left;
this.right = right;
}
}
AVLTreeNode01是AVL树中的每一个节点,包括以下几个组成对象:
- value -- 是节点的值 是用来对AVL树中节点进行排序的
- left -- 是左孩子
- right -- 是右孩子
- height -- 是该节点所对应的子树中的高度
1.2 树的高度
private int height(){
if(this!=null){
return this.height;
}
return 0;
}
public int height(){
return height(root);
}
关于高度,有的地方将空二叉树的高度是1,而本文采用维基百科上的定义,树的高度为最大层次,即空的二叉树,非空二叉树的高度等于它的最大层次(根的 层次为1,根的子节点的层次为2,依次类推)。
1.3 比较大小
//比较两个数的大小
private int max(int a, int b) {
return a > b ? a : b;
}
2.旋转
如果在AVL数中进行插入或者删除节点后,可能会导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态。LL(左左),LR(左右),RR(右右)和RL(右左)。下面给出它们的示意图:
上面的四棵树都是失去平衡的AVL树,从左往右的情况依次是:LL、LR、RL、RR。除了上面的情况之外,还有其他的失去平衡的树AVL树,如下图:
上面的两张图都是为了便于理解,而列举的关于失去平衡的AVL树的例子,总的来说,AVL树失去平衡的情况一定是LL,LR,RL,RR者4种之一,它们都有各 自的定义:
-
LL:左左,插入或者删除一个节点后,根节点的左子树的左子树还有非空节点,导致根的左子树的高度比根节点的右子树的高度大于1,导致AVL树失去了平衡。
例如:在上面的LL情况中,由于根节点(8)的左子树(4)的左子树(2)还有非空子节点,而根节点(8)的右子树(12)没有子节点;导致了根节点(8)的左子树的高度比根节点(8)的右子树(12)高2。
-
LR,又称为右右,插入或者删除一个节点之后,根节点的左子树的右子树还有非空节点,导致根的左子树的高度比根的右子树的高度大于1,导致AV树失去了平衡。
例如,在上面LR情况中,由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
-
RL,又称为右左,插入或删除一个节点后,根节点的右子树的左子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RL情况中,由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。 -
RR,又称为右右,入或删除一个节点后,根节点的右子树的右子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RR情况中,由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
如果在AVL树中进行插入或者删除节点后,可能导致AVL树失去平衡,AVL树失去平衡以后,可以通过旋转使其恢复平衡;
下面介绍LL(左左),LR(左右),RR(右右),RL(右左)这四种情况对应的旋转方法:
2.1 LL的旋转
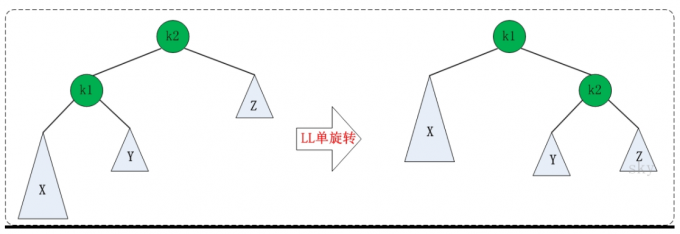
LL失去平衡的情况,可以通过一次旋转让AVL树恢复平衡
图中左边是旋转之前的树,右边是旋转之后的树,从中可以发现,旋转之后的树又变成了AVL树,而且该旋转只需要一次即可完成。
对于LL旋转,你可以这样理解为:LL旋转是围绕失去平衡的AVL根节点进行的,也就是K2,而且由于是LL情况,即左左情况,就用手抓着左孩子,即K1使劲 的摇,将K1变成根节点,K2变成K1的右子树,将K1变成根节点,K2变成K1的右子树,K1的右子树变为K2的左子树。
LL的旋转代码
private AVLTree01Node<T> leftLeftRitation(AVLTree01Node<T> k2){
AVLTree01Node<T> k1;
//把根节点的左子节点保存下来
k1=k2.left;
//把左子节点的右子树放到原先根节点的左子节点
k2.left=k1.right;
//随后 将原先的根节点放在其左子节点的右子节点 将其变成根节点
k1.right=k2;
//改变两个节点的高度的值
k2.height=max(height(k2.left),height(k2.right))+1;
k1.height=max(height(k1.left),height(k1.right))+1;
return k1;
}
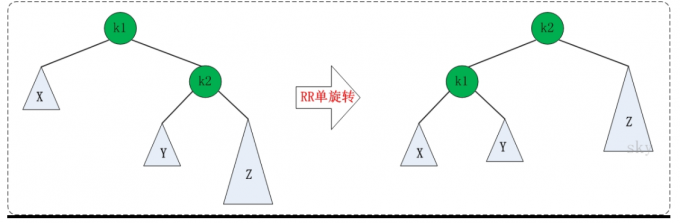
2.2 RR的旋转
理解了LL之后,RR就相当容易理解了,RR是与LL对称的情况!RR恢复平衡的旋转方法:
private AVLTree01Node<T> rightRightRitation(AVLTree01Node<T> k1){
AVLTree01Node<T> k2;
//把根节点的右子节点保存下来
k2=k1.right;
//把右子节点的左子树放到原先根节点的右子节点
k1.right=k2.left;
//随后 将原先的根节点放在其左子节点的右子节点 将其变成根节点
k2.left=k1;
//改变两个节点的高度的值
k2.height=max(height(k2.left),height(k2.right))+1;
k1.height=max(height(k1.left),height(k1.right))+1;
return k2;
}
2.3 LR的旋转
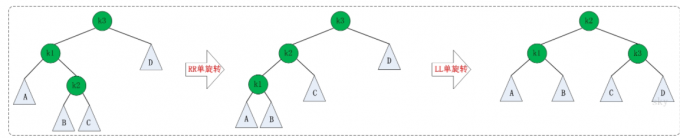
LR失去平衡的情况,需要经过两次旋转才能让AVL树恢复平衡。如下图:
第一次旋转是围绕K1进行的RR旋转,第二次是围绕K3进行的LL旋转。
LR的旋转代码
private AVLTree01Node<T> leftRightRitation(AVLTree01Node<T> k3){
//首先对根节点的左子树进行RR的旋转
k3.left=rightRightRitation(k3.left);
//然后对根节点k3进行LL的旋转
return leftLeftRitation(k3);
}
2.4 RL的旋转
RL是与LR的对称情况! RL的恢复平衡的旋转方法如下:
第一次旋转是围绕k3进行的LL旋转,第二次是围绕k1进行的RR旋转。
private AVLTree01Node<T> rightLeftRitation(AVLTree01Node<T> k3){
//首先对根节点的右子树子树进行LL的旋转
k3.left=leftLeftRitation(k3.right);
//然后对根节点k3进行RR的旋转
return rightRightRitation(k3);
}
3.插入
插入节点的代码
//插入节点的代码
private AVLTree01Node<T> insert(AVLTree01Node<T> node,T value){
if(node==null){
//新建节点
node=new AVLTree01Node<T>(value,null,null);
if(node==null){
System.out.println("ERROR: create avltree node failed!");
return null;
}
}else{
int cmp=value.compareTo(node.value);
if(cmp<0){ //应该将value插入到左子树的情况
node.left=insert(node.left,value);
//插入节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.left)-height(node.right)>1){
//然后递归退回到当某个节点的左右子树的高度不平衡的那个节点
//因为插入操作是在之前执行的 所以 该插入节点一定位于高度不平衡的节点的左子节点内
if(value.compareTo(node.left.value)<0){
//说明应该进行LL旋转
node=leftLeftRitation(node);
}else{
node=leftRightRitation(node);
}
}
}else if(cmp>0){ //应该添加到右子树的情况
node.right=insert(node.right,value);
//插入节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.right)-height(node.left)>1){
if(value.compareTo(node.right.value)>0){
node=rightRightRitation(node);
}else{
node=rightLeftRitation(node);
}
}
}else{ //cmp=0
System.out.println("添加失败 不允许添加相同的节点");
}
}
node.height=max(height(node.left),height(node.right));
return node;
}
//对添加方法进行重载
public void insert(T value){
root=insert(root,value);
}
4.删除节点
删除节点的代码
/**
* 删除AVL树中的节点
* @param node AVL树的根节点
* @param delNode 待删除的节点
* @return 删除以后的根节点
*/
private AVLTree01Node<T> remove(AVLTree01Node<T> node,AVLTree01Node delNode){
//如果根节点为空 或者没有要删除的节点 直接返回null
if(node==null || delNode==null){
return null;
}
//判断要删除的节点位于左子树还是右子树
int cmp=delNode.value.compareTo(node.value);
if(cmp<0){ //说明待删除的节点在左子树
node.left=remove(node.left,delNode); //递归进行删除
//删除节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.right)-height(node.left)>1){
//这里要进行判断是进行哪一种旋转 因为我们不确定现在这个节点的右子树的子节点哪个高度高使得不平衡
AVLTree01Node<T> r=node.right;
if(height(r.left)>height(r.right)){
node=rightLeftRitation(node);
}else{
node=rightRightRitation(node);
}
}
}else if(cmp>0){ //说明待删除的节点在右子树
node.right=remove(node.right,delNode);
//删除节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.right)-height(node.left)>1){
AVLTree01Node r=node.right;
if(height(r.left)>height(r.right)){
node=leftLeftRitation(node);
}else{
node=leftRightRitation(node);
}
}
}else{ //当前节点就是要删除的节点
//tree的左右孩子都非空
if(node.left!=null && node.right!=null){
if(height(node.left)>height(node.right)){
//如果tree的左子树比右子树高
//则找出当前节点所对应的树的右子树的最小节点
//将该节点的值赋值给当前节点 删除该最小节点
AVLTree01Node<T> min=delRightTreeMin(node.right);
node.value=min.value;
node.right=remove(node.right,min);
}
}else{
AVLTree01Node<T> temp=node;
node=(node.left!=null)?node.left:node.right;
temp=null;
}
}
return node;
}
//重载一下删除方法
public void remove(T value){
AVLTree01Node<T> node;
//这里最好进行一下判断 先去查找 如果查找不为空 则在进行删除
if((node==search(root,value))!=null){
root=remove(root,node);
}
}
/**
* @param node 传入的节点(当作树的根节点) 这里传入的应该是要删除节点的右子节点
* @return 返回以node为根节点的树的最小节点的值
*/
public AVLTree01Node delRightTreeMin(AVLTree01Node node) {
AVLTree01Node target = node;
//循环的查找左子节点 就会找到最小值
while (target.left != null) {
target = target.left;
}
return target;
}
所有的java代码
public class AVL01TreeDemo {
private static int arr[]= {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};
public static void main(String[] args) {
int i;
AVLTree01<Integer> tree=new AVLTree01<Integer>();
System.out.println("依次添加");
for (int j = 0; j < arr.length; j++) {
System.out.printf("%d ",arr[j]);
tree.insert(arr[j]);
}
System.out.println();
tree.infixOrder();
}
}
class AVLTree01<T extends Comparable<T>> {
private AVLTree01Node<T> root; //根节点
//获取树的高度
private int height(AVLTree01Node node) {
if (node != null) {
return node.height;
}
return 0;
}
public int height(){
return height(root);
}
//比较两个节点的值的大小
private int max(int a, int b) {
return a > b ? a : b;
}
//LL的旋转代码
private AVLTree01Node<T> leftLeftRitation(AVLTree01Node<T> k2){
AVLTree01Node<T> k1;
//把根节点的左子节点保存下来
k1=k2.left;
//把左子节点的右子树放到原先根节点的左子节点
k2.left=k1.right;
//随后 将原先的根节点放在其左子节点的右子节点 将其变成根节点
k1.right=k2;
//改变两个节点的高度的值
k2.height=max(height(k2.left),height(k2.right))+1;
k1.height=max(height(k1.left),height(k1.right))+1;
return k1;
}
//RR的旋转代码
private AVLTree01Node<T> rightRightRitation(AVLTree01Node<T> k1){
AVLTree01Node<T> k2;
//把根节点的右子节点保存下来
k2=k1.right;
//把右子节点的左子树放到原先根节点的右子节点
k1.right=k2.left;
//随后 将原先的根节点放在其左子节点的右子节点 将其变成根节点
k2.left=k1;
//改变两个节点的高度的值
k2.height=max(height(k2.left),height(k2.right))+1;
k1.height=max(height(k1.left),height(k1.right))+1;
return k2;
}
//LR的旋转代码
private AVLTree01Node<T> leftRightRitation(AVLTree01Node<T> k3){
//首先对根节点的左子树进行RR的旋转
k3.left=rightRightRitation(k3.left);
//然后对根节点k3进行LL的旋转
return leftLeftRitation(k3);
}
//RL的旋转代码
private AVLTree01Node<T> rightLeftRitation(AVLTree01Node<T> k3){
//首先对根节点的右子树子树进行LL的旋转
k3.left=leftLeftRitation(k3.right);
//然后对根节点k3进行RR的旋转
return rightRightRitation(k3);
}
//插入节点
private AVLTree01Node<T> insert(AVLTree01Node<T> node,T value){
if(node==null){
//新建节点
node=new AVLTree01Node<T>(value,null,null);
if(node==null){
System.out.println("ERROR: create avltree node failed!");
return null;
}
}else{
int cmp=value.compareTo(node.value);
if(cmp<0){ //应该将value插入到左子树的情况
node.left=insert(node.left,value);
//插入节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.left)-height(node.right)>1){
//然后递归退回到当某个节点的左右子树的高度不平衡的那个节点
//因为插入操作是在之前执行的 所以 该插入节点一定位于高度不平衡的节点的左子节点内
if(value.compareTo(node.left.value)<0){
//说明应该进行LL旋转
node=leftLeftRitation(node);
}else{
node=leftRightRitation(node);
}
}
}else if(cmp>0){ //应该添加到右子树的情况
node.right=insert(node.right,value);
//插入节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.right)-height(node.left)>1){
if(value.compareTo(node.right.value)>0){
node=rightRightRitation(node);
}else{
node=rightLeftRitation(node);
}
}
}else{ //cmp=0
System.out.println("添加失败 不允许添加相同的节点");
}
}
node.height=max(height(node.left),height(node.right));
return node;
}
//对添加方法进行重载
public void insert(T value){
root=insert(root,value);
}
/**
* 删除AVL树中的节点
* @param node AVL树的根节点
* @param delNode 待删除的节点
* @return 删除以后的根节点
*/
private AVLTree01Node<T> remove(AVLTree01Node<T> node,AVLTree01Node delNode){
//如果根节点为空 或者没有要删除的节点 直接返回null
if(node==null || delNode==null){
return null;
}
//判断要删除的节点位于左子树还是右子树
int cmp=delNode.value.compareTo(node.value);
if(cmp<0){ //说明待删除的节点在左子树
node.left=remove(node.left,delNode); //递归进行删除
//删除节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.right)-height(node.left)>1){
//这里要进行判断是进行哪一种旋转 因为我们不确定现在这个节点的右子树的子节点哪个高度高使得不平衡
AVLTree01Node<T> r=node.right;
if(height(r.left)>height(r.right)){
node=rightLeftRitation(node);
}else{
node=rightRightRitation(node);
}
}
}else if(cmp>0){ //说明待删除的节点在右子树
node.right=remove(node.right,delNode);
//删除节点后 若AVL树失去平衡 则进行相应的调节
if(height(node.right)-height(node.left)>1){
AVLTree01Node r=node.right;
if(height(r.left)>height(r.right)){
node=leftLeftRitation(node);
}else{
node=leftRightRitation(node);
}
}
}else{ //当前节点就是要删除的节点
//tree的左右孩子都非空
if(node.left!=null && node.right!=null){
if(height(node.left)>height(node.right)){
//如果tree的左子树比右子树高
//则找出当前节点所对应的树的右子树的最小节点
//将该节点的值赋值给当前节点 删除该最小节点
AVLTree01Node<T> min=delRightTreeMin(node.right);
node.value=min.value;
node.right=remove(node.right,min);
}
}else{
AVLTree01Node<T> temp=node;
node=(node.left!=null)?node.left:node.right;
temp=null;
}
}
return node;
}
//重载一下删除方法
public void remove(T value){
AVLTree01Node<T> node;
//这里最好进行一下判断 先去查找 如果查找不为空 则在进行删除
if((node=search(root,value))!=null){
root=remove(root,node);
}
}
/**
* @param node 传入的节点(当作树的根节点) 这里传入的应该是要删除节点的右子节点
* @return 返回以node为根节点的树的最小节点的值
*/
public AVLTree01Node delRightTreeMin(AVLTree01Node node) {
AVLTree01Node target = node;
//循环的查找左子节点 就会找到最小值
while (target.left != null) {
target = target.left;
}
return target;
}
//前序遍历AVL树
private void prreOrder(AVLTree01Node node){
System.out.println(node.value);
if(node.left!=null){
prreOrder(node.left);
}
if(node.right!=null){
prreOrder(node.right);
}
}
//中序遍历AVL树
private void infixOrder(AVLTree01Node node){
if(node.left!=null){
infixOrder(node.left);
}
System.out.println(node);
if(node.right!=null){
infixOrder(node.right);
}
}
//对中序进行重载
public void infixOrder(){
if(root!=null){
infixOrder(root);
}else{
System.out.println("当前AVL树为空 无法遍历");
}
}
//对前序进行重载
public void preOrder(){
if(root!=null){
prreOrder(root);
}else{
System.out.println("当前AVL树为空 无法遍历");
}
}
/**
* 递归实现查找AVL树中值为key的节点
* @param node
* @param value
* @return
*/
private AVLTree01Node<T> search(AVLTree01Node<T> node,T value){
if(node==null){
return null;
}
int cmp=value.compareTo(node.value);
if(cmp<0){
return search(node.left,value);
}else if(cmp>0){
return search(node.right,value);
}else{
return node;
}
}
//对查找进行重载
public AVLTree01Node<T> search(T value){
return search(root,value);
}
}
//AVL树的节点(内部类)
class AVLTree01Node<T extends Comparable<T>> {
T value; //节点的值
int height; //高度
AVLTree01Node<T> left; //左孩子
AVLTree01Node<T> right; //右孩子
public AVLTree01Node(T value, AVLTree01Node<T> left, AVLTree01Node<T> right) {
this.value = value;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "AVLTree01Node{" +
"value=" + value +
'}';
}
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号