HDU3038 -How Many Answers Are Wrong
本来只打算刷AC300人以上的,但扫了一眼发现买一送一,AC人数284有个也是跟上道题一样的找出假话数量的
继续跟着邝斌飞刷并查集
HDOJ3038(居然是心心念念HIT哈哈)
妈蛋的最长子序列?这他妈不是动规吗?好像又是个新的玩意
八成是带权并查集,但问题是,4 6 41咋搞啊?之前刷的都是这种没出现的关系就一定正确,但现在前面只要有数据,后面的数哪怕4和6都没出现,但无形中只要输入一组数据,其他哪怕没出现的数据千丝万缕之间就也有个约束,比如4和6他俩之间的和不能超过40(100-28-32)
到这这我就有个感觉,好像一直无脑给pre这个存储父亲节点的数组赋初始值为指向自己就不行了,但好像每输入一行数据就把数据里前两个数字之外的值再重新赋个约束有点der。那我能否搞个二维数组记录,比如q[3][7]=10代表3和7之间最大不能超过10,还是挺der的
又突然想到上一个题里都是判断是否矛盾,那我能否在图里存的时候都存数据的另外那些数据关系,即图中存的是矛盾图,你来一组数据老子就去矛盾图里找。简单画画发现可行,本来以为这道题只能看题解的,没想到居然有可行想法
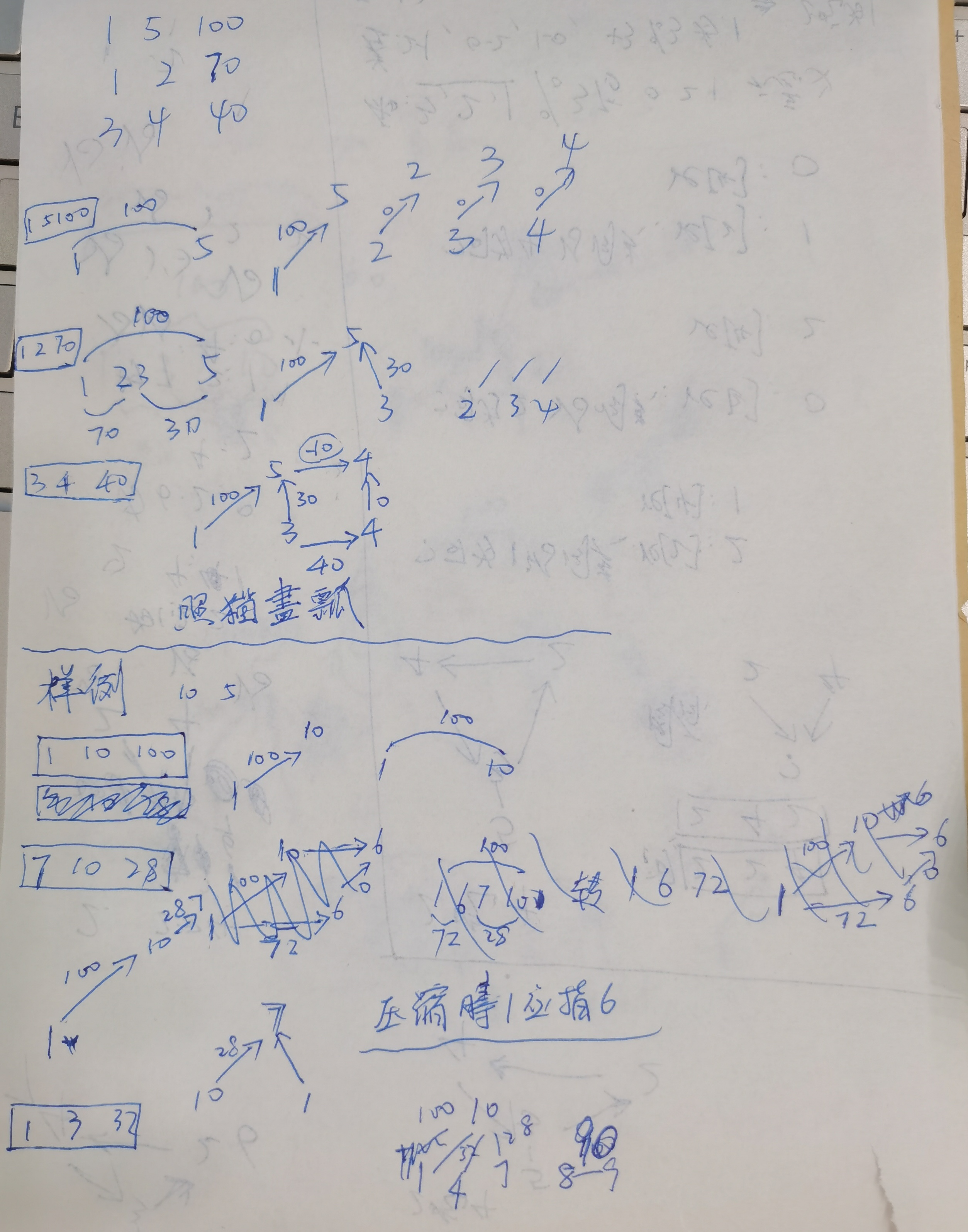
发现依旧不行,压缩时1应指向6,我束手无策了,咋都无法搞未出现的数字,又想下大顶堆?秒pass,我就跟个笨笨咔咔的笨逼似的╮(╯▽╰)╭唉,果断看题解
越看越受打击居然是带权并查集的入门题目~~~~(>_<)~~~~
我先捋顺下我做不下去的卡点:
0、如图中,压缩时1应指向6,但其实是7
1、如果来了一组没出现过的数据,怎么搞
看了几个人的,写的轻描淡写的,脑瓜子里的东西就不能多写点吗?还是说都是显然是我太菜了
md带权并查集太玄妙了,必须自己A出来一个,打算再继续刷
先看了这个逼的,写的根本看不懂,又看这家伙的,然后读了下这个博客,发现解决了我卡点0、,但对于没出现的点的处理方法没搞懂,按照大和尚小和尚自己画出来懂了但根本不理解为啥这样写,再变个型自己根本还是无从下手,以上统称为狗逼博主
接下来又看了下这个博客的(但看着很不爽,其一:这博主也是个虎逼,自己用的啥都不知道,拓展域(扩展)并查集是种类并查集很简单,这题他用的是带权(向量关系)并查集,其二:cnm这个傻逼51cto网站复制代码还得登陆,且复制的还有问题,其三:这傻逼博主解释的那句“比如[1 5]区间和为100 然后后面给出区间[1,2]的和为 200 那肯定就是有问题的了”纯属放屁,说明这个傻逼不知道在哪抄过来的东西东拼西凑自己都没搞懂,但针对他这数据代码居然还是对的。这群人讲的稀里糊涂代码还能对真tm是个人才,这群煞笔全网博客一大抄
又查了下这个博客,这里的例题跟上个题目里的“一个又一个”的第二个知乎那个差不多
又看了这个360图书馆里的文章(好牛逼依旧看不懂),再必应搜搜题解吧,题解,简书博客,都看不懂
找到了这篇文章(姑且叫做高潮博客吧,太开门了讲的),感觉前面有个博客是照这个抄的没抄全,这回读有点懂了,(王秋献:吃七个烧饼不是第七个饱的是有前六个垫底)
还是不咋理解,md上一个题根本就没懂带权并查集,多亏刷了这个题,之前还以为tm买一送一呢结果这tm是送人头
就按照这人写的自己想吧,中间需要自己搭很多桥
注意用脚丫子想都知道这题可以为负数,即数据:
5 2
1 5 100
1 3 200
必然都对
我发现我进入了一个误区,每次没思路看题解的时候,为了理解,都想尽所有可能或者举一些例子,看看他的思路是否都能包括,是否是正确的,但没从宏观想为什么是这样,即从悬崖边过桥,我只验证了过桥后是否能去到我想去的地方,一个验证员而已,真正做题谁给我造桥?真正重要的是怎么在悬崖边造桥。
重新思考:这题起手想到了端点,那开闭区间即可解决这个问题,然后更进一步了解了怎么叫用向量运算构造和维护元素之间的连通以及偏移关系,即高潮博客里说的,也就是合并+压缩路径,再遇到带权并查集,我都往这个思路上想,那现在就剩一个问题,处理端点会了,压缩会了,合并会了,我怎么判断矛盾啊?这么叫矛盾?即当我想合并办事的时候发现你已经能确定了,那我就对能确定的这个玩意,正确就忽略,错误就ans+1,然后判断下一个,那怎么判断这玩意正不正确,
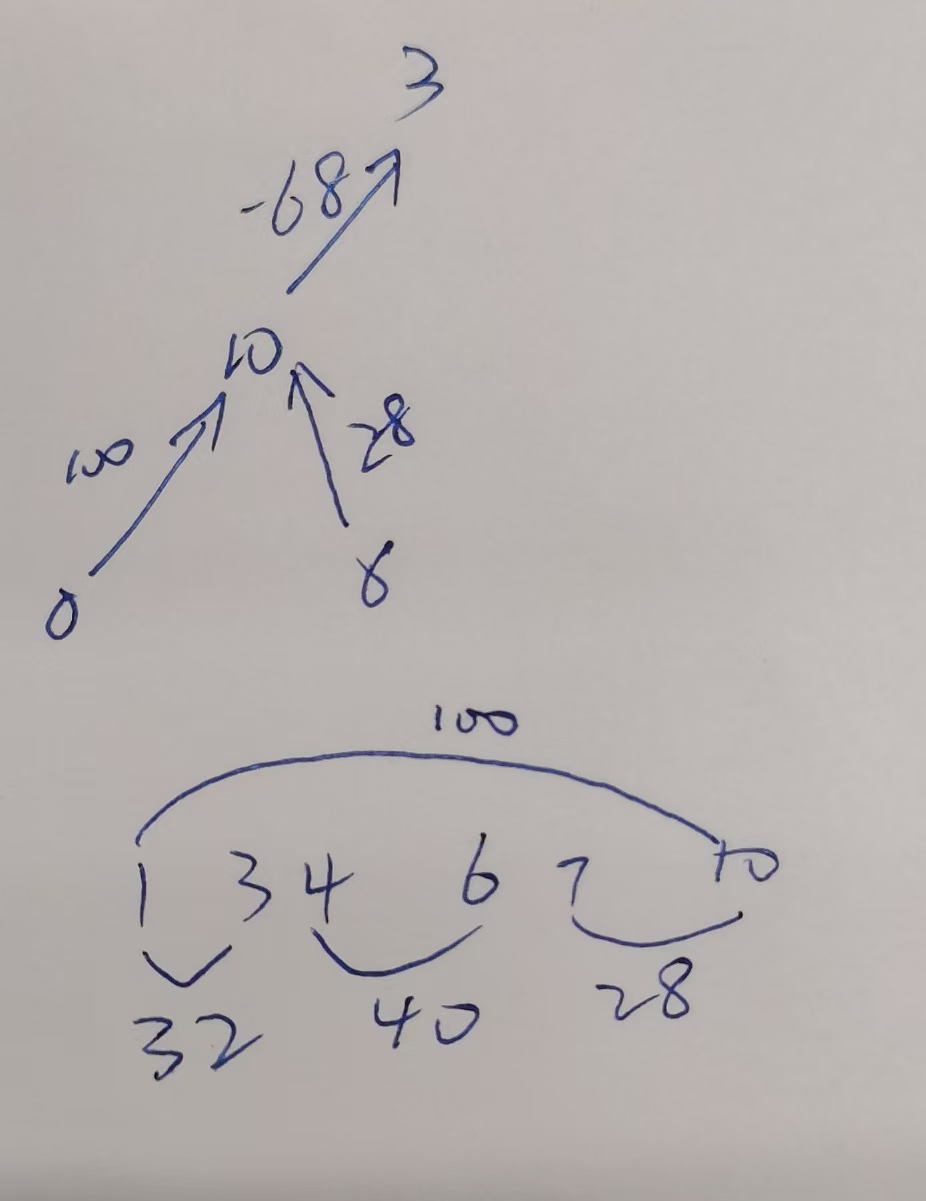
看这个图,为了方便叙述,假定1到10是100,1到3是32,7到10是28,去掉端点的概念,那本应该是4到6距离为40,那现在方便叙述我说3到7是40,假设这句是对的,那只要再说的数不是40就是错的,发现为何可以如此笃定,因为我1,3有关系、7,10有关系、1,10又有关系,这样一来,我3 1 10 7其实就是连通的,“夹逼定理”,重点就出来了找连通:
即我1到3 10 7(尽管是1到6,我为了方便叙述和日后自己回顾简单说成1到7,去掉端点这个事)就都可以确定,分别是32,100,32+40,同理,3到7 10、还有7到10,都可以确定
那我总结下,即你两个数,其中一个可以和其他组织的数有染(啥意思,就是说我的根不是自己),这是正确的,不矛盾的,但如果两个数都各自跟其他组织有染(两个数的根都不是自己),也没问题,但如果这两个有染的根都是同一个人,那即你们各自都跟同个圈子里的人有染,那就是矛盾的,比如总共20个数,我再给图里加组数据叫11 20 30,11到20是30,那3到11可以是任何数,尽管3跟别人有染,11也跟别人有染,但3的有染对象的根是1 3 7 10这几个数里的一个(看你怎么写代码),11有染的根是11和20中的一个,不是同一个。
唉╮(╯▽╰)╭,高潮博客里别人一句话“由上图可知, a和b的根结点相同。所以我们只需验证 a->b是否与题目中给定的值一致。”,我想了好多才懂
感觉至此才能跟前面的几个狗逼博主说的对上(诸如什么“又通过观察可得,当区间为(0,3](红线)时由于3为祖先,不在0,4,2这个并查集内,所以不考虑,那什么时候考虑呢??”、“怎样判断当前区间与前面的区间形成冲突?”、“带权并查集,首先我们要考虑在什么情况下会出错”、“我们需要借助一个载体(根节点)”),他们讲的太不友好了,想起有句话叫什么“世界是反着的社会真理都是反着的反着读就对了”,这些博主都是想完思路给你倒着讲的,那不懂的人谁tm能懂啊,应该讲的是怎么想到这些的。但想这样讲确实很不好写博客,就像我现在这样。
至此有些懂了,自己写代码,估计又是相当坎坷的旅程,顺便说下,合并和压缩,都是数学向量推导出来的,推导过程很简单,但结果运用到这个题目上就很玄妙,所以压缩和合并的那个数学推导结论公式直接理解后拿来用,至于判断是否矛盾,那个结论看似很好懂但实际背后涉及很大的思维过程一定要想懂
开始对着高潮博客写代码
直接AC
AC代码
1 #include<stdio.h> 2 #include<iostream> 3 #define MAX 200001 4 using namespace std; 5 int pre[MAX]; 6 int sum[MAX]; 7 int N,M; 8 int ans; 9 int find(int x) 10 { 11 int tp=pre[x]; 12 if(x==pre[x]) 13 return x; 14 pre[x]=find(pre[x]); 15 sum[x]=sum[x]+sum[tp];//有了上个题的经验 16 return pre[x]; 17 } 18 int main() 19 { 20 while(cin>>N>>M){ 21 ans=0; 22 // for(int i=1;i<=N;i++) 23 for(int i=0;i<=N;i++)//注意:点是1开始但考虑端点开闭区间的事,要从0开始 24 pre[i]=i,sum[i]=0; 25 for(int i=0;i<M;i++){ 26 int a,b,c; 27 cin>>a>>b>>c; 28 a--; 29 int root1=find(a); 30 int root2=find(b); 31 if(root1!=root2){ 32 pre[root1]=root2; 33 sum[root1]=-sum[a]+sum[b]+c; 34 } 35 if(root1==root2){ 36 if((sum[a]-sum[b])!=c) 37 ans++; 38 } 39 } 40 cout<<ans<<endl; 41 } 42 }
注:并查集里上一个题目开始,涉及到“根”,“终极顶点”这些说法,其实叙述不严谨,较真叫的话理论上应该叫终极叶子并不是根,但习惯叫“根”了
###:高潮博客的博主真的太牛逼了,好像是个大佬,关注了他的并查集专栏,附上他的上一个题题解,大概扫了眼感觉不错
###:带权并查集是一个构造向量关系的思维题
###:岛娘:我也不知道为什么,不管以后自己做什么都想把算法竞赛学好,好好学一遍



 浙公网安备 33010602011771号
浙公网安备 33010602011771号