POJ1860-Currency Exchange
继续刷邝斌飞最短路专题
最爱的强大数据的可用平台
难受,洛谷没这题,翻译只能自己来了
百度翻译后题意很简单,唯独这句: For each point exchange rates and commissions are real ,根据样例纯属放屁,
1块钱的2号货币能换1,1块钱的3号货币,且
1块钱的3号货币能换1.1块钱的2号货币。永动机实现自发暴富是吧
开始撸题,感觉相当简单啊

md吃完饭回图书馆,看到对面那个少妇瘦但,屁股好圆润,颜值也还行,主要是站起来的时候,小腹到小穴线条太往里凹了,好像插到底,看到这一幕差点鼻血喷出,直荷尔蒙肾上腺素飙升,看一眼血气上涌。应该算见过唯一一个瘦子有性欲的。可我已经可以克制,过了那个阶段了
题意:百度翻译很好理解,给你
N总共货币种类编号1~N(1<=N<=100),M兑换点(1<=M<=100),S你持有的编号为S的货币(1<=S<=N<=100),V你手里的钱当然是S类型的(0<=V<=1000)
每个兑换点都可以兑换两种货币,且多个兑换点可以兑换同样两种货币。兑换规则是减去佣金乘汇率,比如100块A币种兑换B币种,A到B的佣金是10,汇率是3,则可以兑换(100-10)* 3=270块B币种。
10-2<=汇率<=102,0<=佣金<=100
但始终不知道这句话啥意思,根据直觉像是约束条件告诉你不会SPFA算法(因为听过卡SPFA就是构造菊花图使得多次爆炸队列啥的使得复杂度等同于n^3的贝尔曼福特)?好像也不是,不管这句话
Let us call some sequence of the exchange operations simple if no exchange point is used more than once in this sequence. You may assume that ratio of the numeric values of the sums at the end and at the beginning of any simple sequence of the exchange operations will be less than 10^4.
这题先想是出发点到出发点(单源),没必要弗洛伊德,
再看能否用最经典的迪杰斯特拉,刚学贝尔曼福特的时候,我经过自己琢磨耗费无数心血这个博客里,起初觉得迪杰斯特拉可以处理负权,然后对拍好久发现了,其实不能的原因不是负,而是不能二次进入的问题,关键例子就是唯一路径,看这个例子
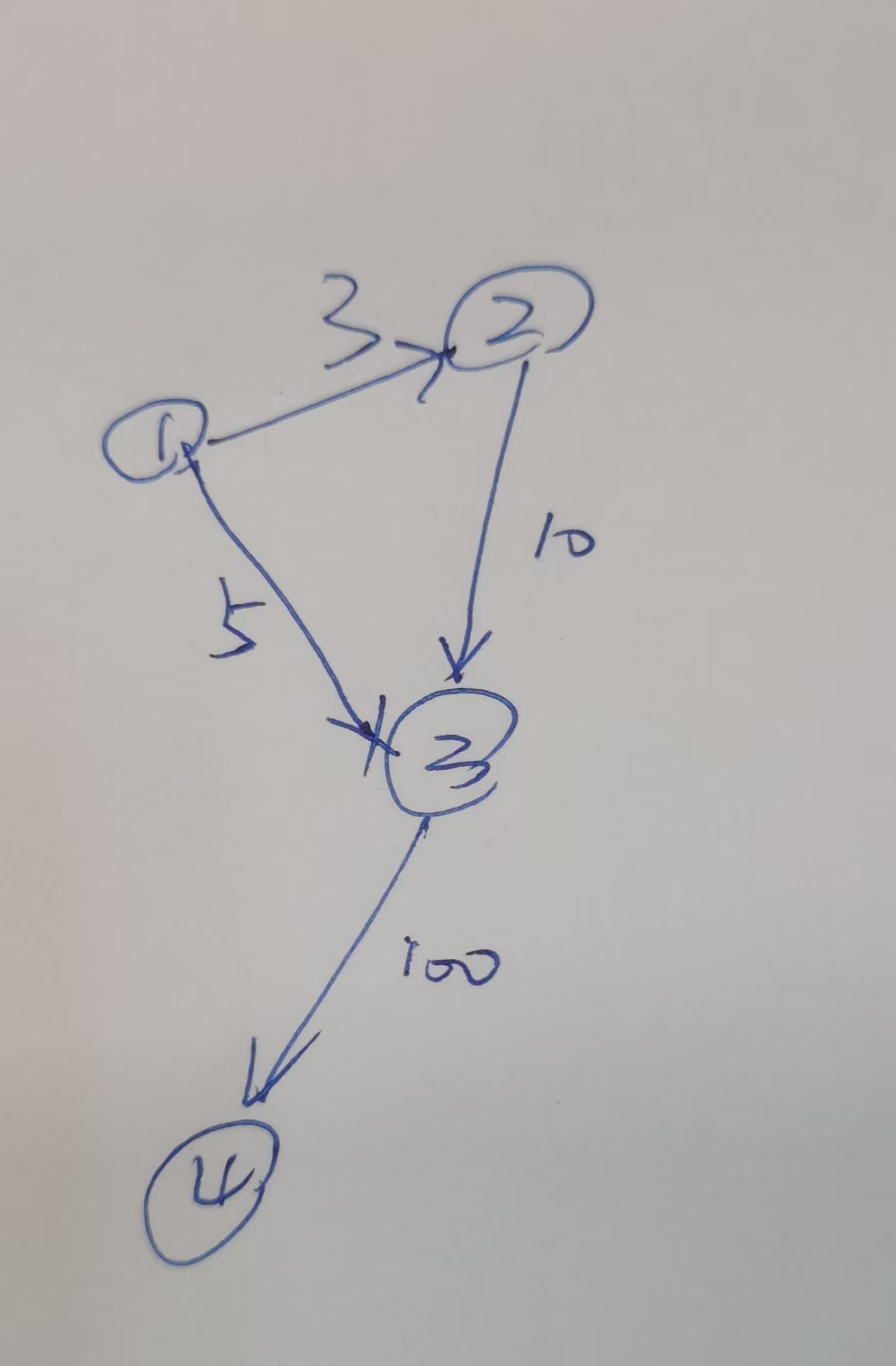
③到④是去往④这个点的唯一路径,即可以当作大众所知的负权问题,也最好判断是用迪杰斯特拉还是用贝尔曼福特,我想尽可能的取最大值,1出发,走3(尽管先走2才是最大),然后此时走4发现是105,但其实应该是1234,最大是113,仿佛最长路径的意思。那我觉得就可以判断是用贝尔曼福特算法了(其实迪杰斯特拉算法思想摆在那,是只能判断最短,而贝尔曼虽说是最短路算法,但本质是可以边*点,能把所有情况都加进来判断,所以你写最长就是最长路径),那篇文章说SPFA学会了但懒得写,这次不管卡不卡SPFA,先写SPFA。
显然有点忘了贝尔曼思想,回顾下。
(为了更快写博客和想思路,都是边想边写博客)
发现不写真是不行,那篇虫洞的SPFA看别人代码后现在一点印象都没,回去再回顾下
感觉朴素数组没啥意思肯定够会写了,直接用vector,用虫洞博客里洛谷那俩人的题解抄语法就行(ljcljc 、wjy666)
但看的时候不明白为何把所有点都加入队列,看了几个博客懂了,知乎解答(不详尽)、说spfa已经死了的傻狗、展开spfa为啥死了的傻狗、参考博客(最完美解答),其实很好理解,最短路径依旧是顶点加入队列,而判断负环其实就已经是多源了,当然要把所有顶点都加入判断一遍。
但具体问题具体分析,这个题已经告诉你从给定的货币开始了,再回到给定的货币,即问题转化为:S点回到S的最长路径。
(后来在我A掉以后写下一个题的时候,发现这个题也要每个点都加入队列,详细见博客)
写了个代码WA了

1 #include<stdio.h> 2 #include<vector> 3 #include<queue> 4 #include<string.h> 5 #include<iostream> 6 using namespace std;//vector必须要有这句 7 struct Edge{ 8 int to; 9 double rate; 10 double commission; 11 } edge; 12 vector<Edge>G[201];//最多100种货币 13 queue<int>q; 14 double D[201]; 15 int flag; 16 void SPFA(); 17 int N,M,S; 18 double V;//money 19 int a,b; 20 int main() 21 { 22 // freopen("zhishu.txt","r",stdin); 23 double rate_ab, commission_ab; 24 double rate_ba, commissiom_ba; 25 while(cin>>N>>M>>S>>V){ 26 while(!q.empty()) 27 q.pop(); 28 flag=0; 29 memset(D,0,sizeof(D)); 30 for(int i=0;i<M;i++){ 31 cin>>a>>b>>rate_ab>>commission_ab>>rate_ba>>commissiom_ba; 32 edge.to=b; 33 edge.rate=rate_ab; 34 edge.commission=commission_ab; 35 G[a].push_back(edge); 36 37 edge.to=a; 38 edge.rate=rate_ba; 39 edge.commission=commissiom_ba; 40 G[b].push_back(edge); 41 }//至此存图结束 42 43 SPFA(); 44 45 if(flag==1) 46 cout<<"YES"<<endl; 47 else 48 cout<<"NO"<<endl; 49 50 } 51 } 52 void SPFA() 53 { 54 q.push(S); 55 D[S]=V; 56 int cnt=0; 57 while(!q.empty()){ 58 int u; 59 u=q.front(); 60 q.pop(); 61 cnt++; 62 for(int i=0;i<G[u].size();i++){ 63 int v=G[u][i].to; 64 double rate=G[u][i].rate; 65 double commission=G[u][i].commission; 66 if(v==S) 67 cnt++; 68 if(cnt==M){ 69 return; 70 } 71 72 if(D[S]>V){ 73 flag=1; 74 return; 75 } 76 // cout<<D[v]<<endl; 77 if((D[u]-commission)*rate>D[v]){ 78 D[v]=(D[u]-commission)*rate; 79 q.push(v); 80 } 81 } 82 } 83 }
对拍代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() { 4 double V; 5 srand(time(NULL));// random_double=rand()/(double)RAND_MAX; 6 V=(rand()%100)/10.0+30;//随机浮点数 7 8 srand(time(0) + (unsigned long long)(new char)); 9 int N=rand()%4 + 1; 10 int M=rand()%3+1; 11 int S=rand()%N+1; 12 13 cout<<N<<" "<<M<<" "<<S<<" "<<V<<endl; 14 for(int i=0;i<M;i++){ 15 int a=rand()%N+1; 16 int b=rand()%N+1; 17 double rate_ab=(rand()%10)/3.0+0.1; 18 double commissiona_ab=(rand()%10)/3.0; 19 double rate_ba=(rand()%10)/3.0+0.1; 20 double commission_ba=(rand()%10)/3.0; 21 cout<<a<<" "<<b<<" "<<rate_ab<<" "<<commissiona_ab<<" "<<rate_ba<<" "<<commission_ba<<endl; 22 } 23 24 }
找个AC博客对拍,生成的随机数据:
3 3 3 39.7 1 2 1.7 3 0.43 0.67 2 3 0.1 1.3 1.8 0.67 2 1 0.1 2 2.4 0
我发现大概是要在货币1和货币2即汇率为1.7的那个兑换点转悠好多次才是答案,我索性先不行那么多,直接将下面AC代码中的68行乘了很大,发现乘10不行,100不行,麻痹的直接乘10000,才过这组数据,而这组数据过了,提交就AC了。但是这个10000跟题目那句10^4的限制范围没关系吧
AC代码 —— 诸多细节见后面的博客
1 #include<stdio.h> 2 #include<vector> 3 #include<queue> 4 #include<string.h> 5 #include<iostream> 6 using namespace std;//vector必须要有这句 7 struct Edge{ 8 int to; 9 double rate; 10 double commission; 11 } edge; 12 vector<Edge>G[101];//最多100种货币 13 queue<int>q; 14 double D[101]; 15 int flag; 16 void SPFA(); 17 int N,M,S; 18 double V;//money 19 int a,b; 20 int main() 21 { 22 // freopen("zhishu.txt","r",stdin); 23 double rate_ab, commission_ab; 24 double rate_ba, commissiom_ba; 25 while(cin>>N>>M>>S>>V){ 26 while(!q.empty()) 27 q.pop(); 28 flag=0; 29 memset(D,0,sizeof(D)); 30 for(int i=0;i<M;i++){ 31 cin>>a>>b>>rate_ab>>commission_ab>>rate_ba>>commissiom_ba; 32 edge.to=b; 33 edge.rate=rate_ab; 34 edge.commission=commission_ab; 35 G[a].push_back(edge); 36 37 edge.to=a; 38 edge.rate=rate_ba; 39 edge.commission=commissiom_ba; 40 G[b].push_back(edge); 41 }//至此存图结束 42 43 SPFA(); 44 45 if(flag==1) 46 cout<<"YES"<<endl; 47 else 48 cout<<"NO"<<endl; 49 50 } 51 } 52 void SPFA() 53 { 54 q.push(S); 55 D[S]=V; 56 int cnt=0; 57 while(!q.empty()){ 58 int u; 59 u=q.front(); 60 q.pop(); 61 cnt++; 62 for(int i=0;i<G[u].size();i++){ 63 int v=G[u][i].to; 64 double rate=G[u][i].rate; 65 double commission=G[u][i].commission; 66 if(v==S) 67 cnt++; 68 if(cnt==M*10000){ 69 return; 70 } 71 72 if(D[S]>V){ 73 flag=1; 74 return; 75 } 76 // cout<<D[v]<<endl; 77 if((D[u]-commission)*rate>D[v]){ 78 D[v]=(D[u]-commission)*rate; 79 q.push(v); 80 } 81 } 82 } 83 }
妈的我发现为啥我费那么大心血搞透彻的算法,比如最短路迪杰斯特拉不能处理负边的本质,比如迪杰斯特拉先加入的并不是最优解之类的这些,怎么到别人那一句两句就轻描淡写带过了,都这么牛逼的么?好像学起来都很轻松的样子。上面那个AC博客里写的那几句屁话他自己真能理解么??能的话那我真的是比他理解能力差好几个层次,我跟他表述的东西根本不在一个维度,这也说明了,为啥很多博客写的讲解题解啥的,跟屁话一样,因为我能理解的点都只能靠我自己千辛万苦推导试验出来才行。如果没有之前的那些坎坷,这题我连迪杰斯特拉还是贝尔曼都不知道
但实际代码,这人用的是贝尔曼,我用的是SPFA,并不涉及我那个进入多少次的问题,再看其他博客
麻痹的这题没看到一个SPFA,全是贝尔曼,题解少之又少,不管了
此题OVER
但留个我的思考吧,就比如我生成的这个样例,什么是最坏情况呢,这个样例已经有点意思了,进一步来说,当持有3货币时,去换到2,此时2无论是走汇率为0.43那个兑换点还是走汇率为0.1那个兑换点都会使得资金变少,但从2换到1以后,1再到2的汇率会使得资金变多,那么此时想一个极限情况,100种货币即100个点,如果每一个点兑换过去,都是题目给出的最小的0.01汇率,那么,100个就是10-200倍的本金,如果只有一个兑换点,可以使得资金变多,那最坏情况就是循环兑换你这个兑换点,汇率取可以变多的最小值,即1.000001?,姑且用1.1,那么,10-200倍的本金V,乘1.1的多少次方才能回到本金V,回到本金后再多兑换一次就变多了,本金约掉,就是我循环的最多次数,n为这个最多次数的话,n就是:1.1 * n=1 /(10-200)。。先大概想到这,我这强迫症必须给上面那句提到的不理解的英文强行解释下,姑且理解成:
一次货币A到货币B的兑换称之为简单操作,所有输入数据,从头到尾,每个货币简单操作后,累和,跟在一个操作上循环兑换的次数,之比,不超过10000。感觉不太对,不管了
###:随机浮点数
###:

画的图有点抽象,像逼,凑活看吧
###:更新:更新想法来自于这个博客(题目:Arbitrage)
发现哪怕只有4种货币,我持有1号货币,然后分别有5家兑换点,分别可兑换:12、13、14、23、34
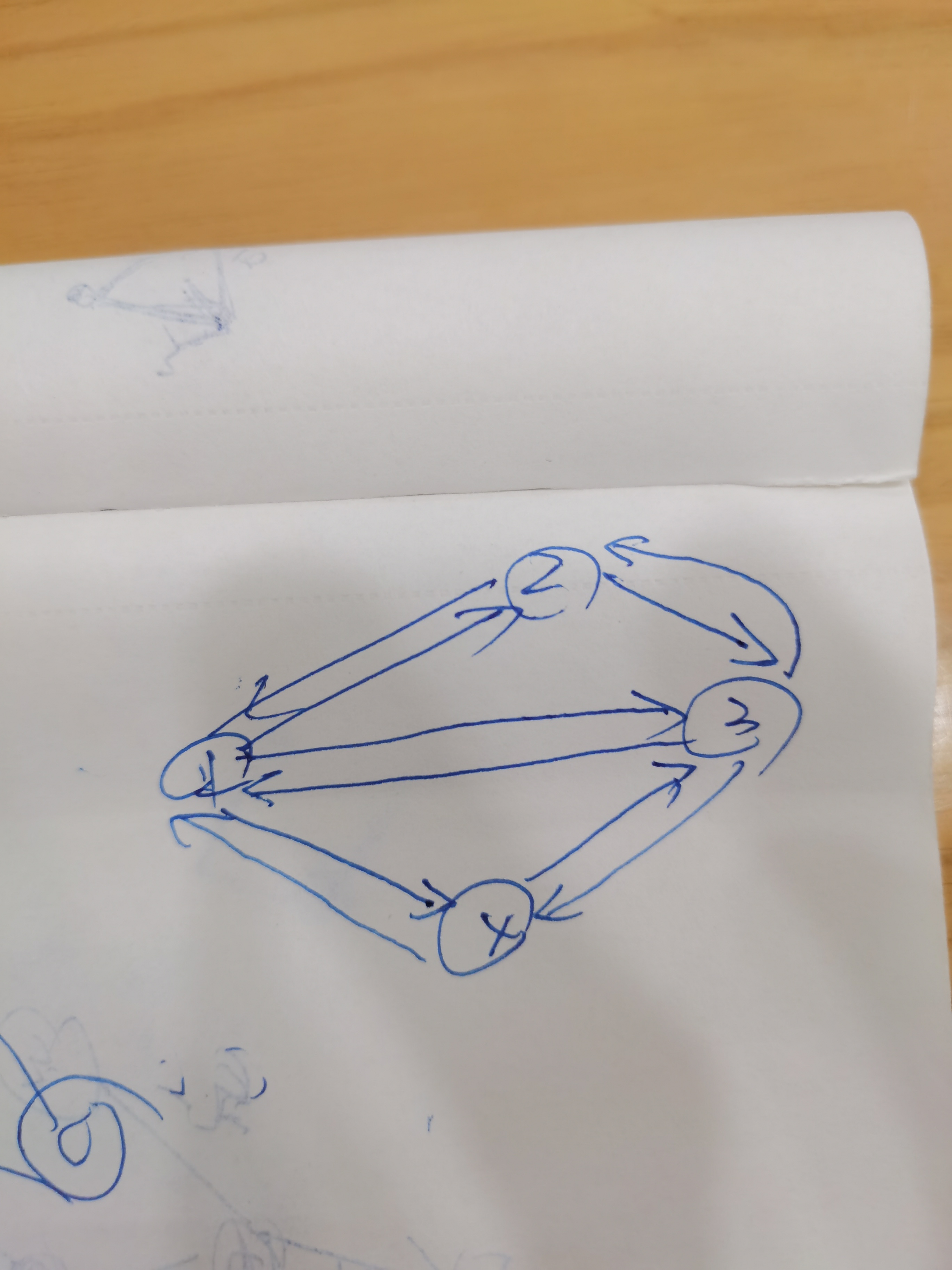
那我发现仅仅只有4种货币,5个兑换点的情况,就有13种
只涉及一个兑换点:
12→21
13→31
14→41
只涉及两个兑换点:
12→23→32→21 (12和21是一个兑换点,23和32是一个兑换点)
13→32→23→31
13→34→43→31
14→43→34→41
只牵扯三个兑换点:
12→23→31 (12、23、31是不同的三个兑换点)
13→32→21
13→34→41
14→43→31
只牵扯四个兑换点:
12→23→34→41
14→43→32→21
这还是最好的,如果汇率都很低,只有一个汇率高的,那还要再某几个高汇率的兑换点之间循环多次兑换,来弥补走过低汇率兑换点导致的本金变少的情况
###:另外发现了一个相当大的问题,见那个题目是Arbitrage的博客
###:诸多细节见后面的博客




 浙公网安备 33010602011771号
浙公网安备 33010602011771号