POJ3660-Cow Contest
继续刷邝斌飞最短路专题(看了下就刷10个题吧)
我最爱的可用平台没有这题
读完发现这JB玩意跟图论有关系吗~~~~(>_<)~~~~

昨天看电报大爆射7次郎今天来图书馆晚了点,逐渐没啥好片子了
将样例给的5个数弄成图,瞎JB划了划了,发现啊,正着找一遍最长路径,反存图再找一遍最长路径,每段路经都假设距离是1,重叠部分貌似就是答案,样例正:125,反存图:5234,倒过来4325,发现25重叠了。感觉思路不对头有点随意,且好像是字符串匹配呢?换个思路,再举个例子,734592,其中73顺序随意,92顺序随意,只有45可确定是在中间,画图发现进入5的只有一条线,那上一个也是进入5只有一条线。妈的这题是不是太简单了,入度为1就是一个确定点,n个入度为1的点,直接答案就是n+1啊。
这题在洛谷上是普及+/提高,会这么简单???
不对,如果7>3,4>9,两个入度为1的点,但根本确定不了任何顺序,那再加个条件呢?如果大小顺序的数据小于n-1直接No,那加一个4>3发现入度为1的点只有9,但还是啥位置也确定不了
本来想看题解,发现洛谷标签真的好,去学下拓扑排序

其实时刻觉得这些对找工作没用,为何还要每天学,给自己一个交代执念吧,岛娘:不管以后做什么算法竞赛一定要学好 哎所有的东西都似曾相识,之前刷过但稀里糊涂的,考研貌似是操作系统也有这些 讲的 高中7班数学老师: 记者啊 美国没同情流浪汉完了, 可以说我挫不可以说我的学生 我的话有一个人人帮助就成功了 10班: 自己想,哪想不出来搭桥接上,下次才能做出来 读那个以为是狗屁文章:世界是反着的,发现说的挺对的,结论也是,如果事先看题解,由于踩的坑不多,根本无法理解结论,结论只是简简单单一句话背后的推导逻辑是关键,而这结论在自己实际想的时候又会影响自己推导,因为总觉得并不是渐进的能想到的步骤,总觉得会不会前面还有步骤,脑子里总有答案的痕迹阴影。就算看懂下次又肯定想不出来。而没思路想看提示却跟没没有,全网都是给你最后清爽的结论,很不利于学习成长,打算写一个循序渐进有思考过程的博客,这样别人没思路看我博客的时候,读到哪有思路,跟自己想的地方接上了,就可以自己去写了。我就没思路的时候都不敢太搜不敢看太多,都是放大网页300%,一句一句看,既不希望看到最后结论,又希望看到些小提示 比如Heavy Transportation那个题,我A完才勉强看懂那些题解,详见那篇博客
讲的一坨屎,简单介绍,咋感觉这题给的就是拓扑排序结果呢我靠!去你妈拓扑,拓个JB耽误老子时间。
但发现拓扑也给了我启发
对于样例,画图发现,2这个点,入度是3,那有三个比他大的,431,那2就拍第四位,5这个点,入度为1,发现看入度不行了,重新来。
对于样例,2这个点,按照经过点最多的方法来走,4到2经过3, 3的入度为1,那3记为第二个点??此时看2这个点,有入度为0的点1,入度为1的点3,那么2就是第四个点??5就是3的携带数字+1??也不对问题太多了,两个入度为0的4和1没考虑,3根本不是第二个点
用上面的例子再划了划了,又有点想法,如下
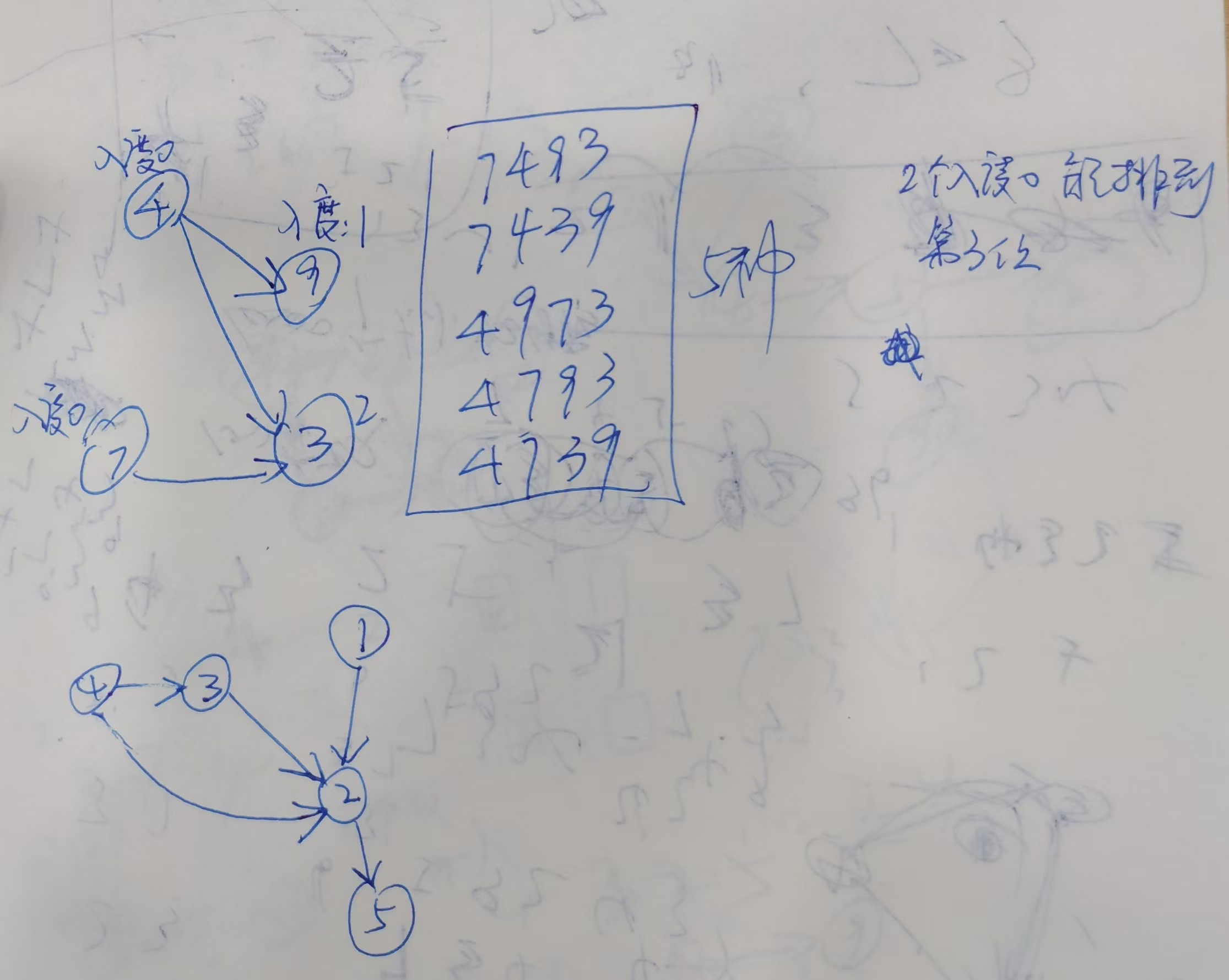
我发现图里上面的例子,4和7入度都是0,但是7最差却可以排到第三位,也就是说49之后,
突然想到个词,上面简单介绍里的这句:“只有在指向该顶点的所有有向边对应的活动结束,该顶点所代表的事件才发生”,也是之前学过的现在忘记了的貌似叫关键路径的东西,但略有差异,这里是4和7同为0入度,那4走9后,同入度的7再开始,即7可以在第3位
4可以排到第1、2位
7可以排到第1、2、3位
9可以排到2、3、4位
3可以排到3、4位
再看图里第二个例子,1和4入度为0,争夺第1、2位
但由于4后有个3,4后有个2,2在1后,所以若先把3走了,4和3先发生,那1就排到了第3位,至此分析0入度的1可以在1、2、3位,0入度的4可以在1、2位
3的入度为1,那位置就去完全取决于4,3可以在1+1、2+1,即第2、3位
2取决于所有入度的点的位置最大值+1(这里我也觉得没道理,但仔细想想就是这样的,这个结论就属于要自己推的,因为他根本没有逻辑,只是例子综合起来结论就是这样的)
5入度为1,位置只取决于2,那就是第5位
心里已经有结论了,再随便构造一个:
入度为0的点有2个,
入度为1的点有1个,
入度为2的点有2个,
入度为3的点有1个
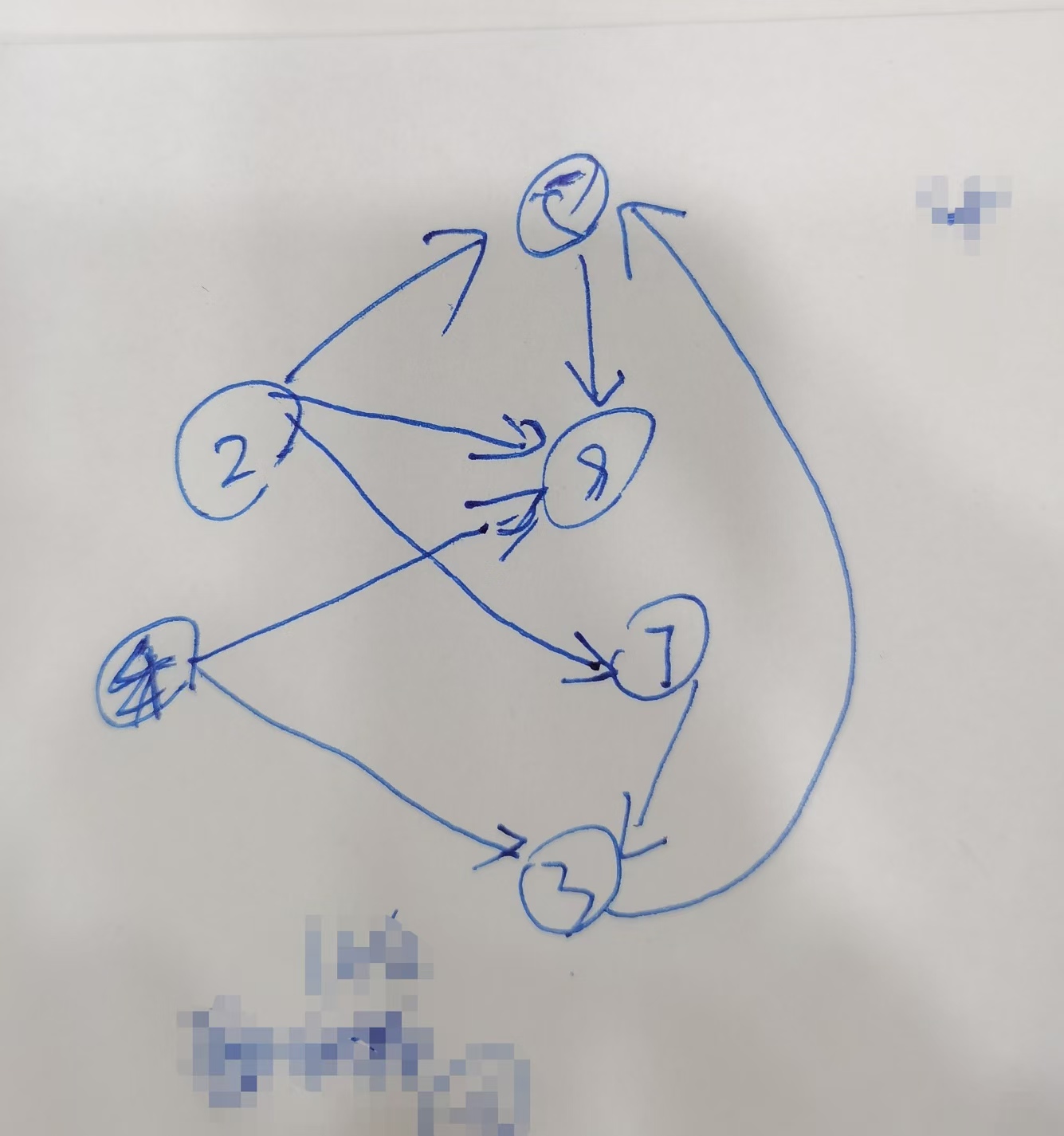
实际验证是后三位359可以确定
再用我的结论跑一遍
首先,2和4争夺首位
如果2为第1位:
2不走,4可以是第2位
2走个7,4在第3位(2不能先走4后面的5 9)
如果4为第1位:
4不走,2为第2位(4不能先走2后面的3 9)
至此,
2可以在1、2
4可以在1、2、3

脑子好笨,之前L明珠给我讲分工任务的时候,开户开网银啥的,他能很好的弄清,而我问了好几遍,也搞不懂,什么不能同一个机构下,好乱。其实我想了很多,因为网银那lansiyang讲的并不是他们想的那么简单,后期也验证我说的比业务老师说的都对。但简单问题脑子好笨好笨
继续(此时有24、274、42)
然后入度为1的7,只取决于2,2是1、2
直接用前度的+1,,但数据太少我不确定少不少情况,保险起见再来一个上一个前度总数,即2和4这两个
至此
7可以在2、3
继续(此时有247、274、427)——(我tm研究到现在咋感觉跟最短路没关系呢艹)
4和7找到位置后,3没度了,看3
3只跟4和7有关:4是1、2、3——7是2、3
至此发现前度+1不太行了,总不能是2、3、4吧
那前面度总合,0度的2和4,1度的7,到3是第4位?那对于上一个7的判断又不行了
(哈哈面向答案想思路)
那我再想个思路,将和入度为1的区分开,这里入度为2的取4和7的最大位置+1
至此
3可以在4
继续
开始看5,3取完出去的度减一就剩下5了,5只与2和3有关
2是1、2——3是4
度不是1,那我取最大值加1,就是5
至此
5可以在5
继续
看9,度不是1,跟4、2、5有关,
4是1、2、3
2是1、2
5是5
最大值+1,即为6
至此
9可以在6
我太笨了,只能想到这了,写完之后如果WA就看洛谷题解咋写的
还有别人AC这个题也要我想这么久么?????(先写一遍,然后看洛谷思路步骤)
感觉我的思路好差
想半天写不出来,好挣扎不想写了,看说拓扑排序,但又说是弗洛伊德变形,传递闭包(离散数学),好高级想学下
强迫症还是想先写下
一开始觉得广搜不行,比如图里的点2和4压入队列,2第一个弹出后找7,但以为4还没有判断位置没法搞啊(后来仔细想下,首先这真的是广搜么?是深搜吧,后来发现确实是广搜。其次,4没判断就没法判断7么?)
又觉得要深搜,先纵向把入度为0的搜完,弹2弹4,然后再判断入度为1的7
好像领悟到了上一个题那个洛谷题解里说的广搜不知道路径那句话了
真的没法写,放弃了,就拿247这几个数来说,
2先上,然后2的出度7和4看哪个先上,若7上,再看3,发现在4后,那憋着,且4没上过,那就4进来,至此274。若4先上,然后走2的出度7,247。
然后还能再4先来,(相当于多次n次?的搜索)...427,疯了彻底想不出来了。看题解
(而且,看点的出度也不行,即后面有几个,看看能否确定这个点的位置,4后有359,但4依旧确定不了位置,前面2和7都可以先加进来,尽管4的入度为0 )
例子举差了,要按顺序!!

6 8 1 4 1 6 1 5 3 2 3 6 4 6 5 2 2 4
洛谷这人的题解讲解真的太好了!!还用上了bitset优化,又去查了下知乎传递闭包,发现也挺简单的,但对比下,位不位运算的bitset有啥好处么??感觉没啥差别,具体用到再体会吧,先搁置。
f[i][j]=f[i][j]|f[i][k]&f[k][j]; 真巧妙啊,我一直不知道怎么判断某点比他经过指向好几个数后的那个数大
这文章里说弗洛伊德可以用bfs/dfs, 想破脑袋也不知道弗洛伊德咋用搜索写,脑子想的好累。感觉代码能力已经有质的飞跃了,该多读读别人的思路和代码补充下知识了(poj的discuss有人说不就暴力么,叫那么好听,其实写出来是暴力的写法,但蕴含的算法思路真的牛逼,相当玄妙,可不是暴力这么简单!!!单单仨for的顺序当初理解的时候就贼鸡巴难想)
再看个搜索的,这个做法太高潮了,看懂意思就自己写下代码(但注意,感觉这个只是解决这个题,跟弗洛伊德的搜索写法好像还完全不是一个东西,这里的搜索纯线性往下走,并没有插点的步骤吧?貌似是这样)代码非常好写,一次AC(想过可不可以不反存图,每次dir[a][b]和dir[b][a]都赋1,意思是只要比我大比我小都算能确定,然后一个dfs,但发现不行,样例3指向2,这样就会2指向3,又有1指向2,可是1和3无法确定)
AC代码
1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 using namespace std; 5 int i_can_win[101];//对于100这个牛来说,记录下我能打败的牛的数量 6 int i_cannot_win[101]; 7 int dir[101][101]; 8 int reverse_dir[101][101]; 9 int N,M; 10 int a,b; 11 int p; 12 void dfs_for_dir(int x); 13 void dfs_for_reverse_dir(int x); 14 int vis[101];//防止多加,比如2指向3,3指向4,2直接指向4,就怕4在2的can_win记录里会加两遍 15 int main() 16 { 17 // freopen("zhishu.txt","r",stdin); 18 while(cin>>N>>M){ 19 20 memset(i_can_win,0,sizeof(i_can_win)); 21 memset(i_cannot_win,0,sizeof(i_cannot_win)); 22 memset(dir,0,sizeof(dir)); 23 memset(reverse_dir,0,sizeof(reverse_dir)); 24 25 for(int i=0;i<M;i++){ 26 cin>>a>>b; 27 dir[a][b]=1; 28 reverse_dir[b][a]=1; 29 }//输入数据完毕 30 31 for(int i=1;i<=N;i++){ 32 memset(vis,0,sizeof(vis)); 33 p=i; 34 dfs_for_dir(i); 35 dfs_for_reverse_dir(i); 36 } 37 int ans=0; 38 for(int i=1;i<=N;i++){ 39 if(i_can_win[i]+i_cannot_win[i]==N-1) 40 ans++; 41 } 42 cout<<ans<<endl; 43 } 44 } 45 46 void dfs_for_dir(int x) 47 { 48 for(int i=1;i<=N;i++){ 49 if(dir[x][i]==1&&vis[i]==0){ 50 vis[i]=1; 51 i_can_win[p]++; 52 dfs_for_dir(i); 53 } 54 } 55 } 56 void dfs_for_reverse_dir(int x) 57 { 58 for(int i=1;i<=N;i++){ 59 if(reverse_dir[x][i]==1&&vis[i]==0){ 60 vis[i]=1; 61 i_cannot_win[p]++; 62 dfs_for_reverse_dir(i); 63 } 64 } 65 }
真的是看懂思路就开始写比较好,不要先看别人代码,不然真的影响自己写。想破脑袋没思路,看洛谷题解就是做好的衔接桥梁
感觉两种方法学差不多了,至此再自己写遍传递闭包弗洛伊德代码收尾
代码涉及到的小细节,关于 if(a||(b&&c)) bc那有没有必要加括号,测试代码:

1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 using namespace std; 5 int i_can_win[101];//对于100这个牛来说,记录下我能打败的牛的数量 6 int i_cannot_win[101]; 7 int dir[101][101]; 8 int N,M; 9 int a,b; 10 int main() 11 { 12 //// freopen("zhishu.txt","r",stdin); 13 // while(cin>>N>>M){ 14 // 15 // 16 // for(int i=0;i<M;i++){ 17 // cin>>a>>b; 18 // dir[a][b]=1; 19 // }//输入数据完毕 20 // 21 // for(int k=1;k<=N;k++) 22 // for(int i=1;i<=N;i++) 23 // for(int j=1;j<=N;j++){ 24 // if(dir[i][j]||dir[i][k]==0&&dir[k][j]==0) 25 // } 26 // } 27 28 for(int i=0;i<=1;i++) 29 for(int j=0;j<=1;j++) 30 for(int k=0;k<=1;k++) 31 // if( (i||j&&k) != (i||(j&&k)) ) 32 if( (i&&j||k) != (i&&(j||k)) ) 33 cout<<i<<j<<k<<endl; 34 }
妈的这传递闭包短短几行代码是真难想啊(再次证明不仅仅看上去的暴力那么简单),写来写去发现不会写了,真的是,不是自己想出来的代码就是白扯
第一次居然WA了!!

1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 using namespace std; 5 int can_determined[101]; 6 int dir[101][101]; 7 int N,M; 8 int a,b; 9 int vis[101][101]; 10 int main() 11 { 12 // freopen("zhishu.txt","r",stdin); 13 while(cin>>N>>M){ 14 15 memset(dir,0,sizeof(dir));//如果不是多组输入则不用这句话 16 for(int i=0;i<M;i++){ 17 cin>>a>>b; 18 dir[a][b]=1; 19 }//输入数据完毕 20 21 memset(can_determined,0,sizeof(can_determined)); 22 memset(vis,0,sizeof(vis));//如果不是多组输入则不用这句话 23 for(int k=1;k<=N;k++) 24 for(int i=1;i<=N;i++) 25 for(int j=1;j<=N;j++) 26 if( dir[i][j] || (dir[i][k]==1&&dir[k][j]==1) ) 27 { 28 if(vis[i][j]==0 && vis[j][i]==0){ 29 vis[i][j]=1; 30 vis[j][i]=1; 31 can_determined[i]++; 32 can_determined[j]++; 33 // cout<<" "<<k<<" "<<i<<" "<<j<<" "<<can_determined[j]<<endl; 34 } 35 } 36 37 int ans=0; 38 for(int i=1;i<=N;i++) 39 if(can_determined[i]==N-1) 40 ans++; 41 42 43 cout<<ans<<endl; 44 } 45 46 }
反例依旧是我举的那个
6 8 1 4 1 6 1 5 3 2 3 6 4 6 5 2 2 4
忘记松弛了。加了也不对,真写的我头晕目眩,写着写着又跟正图搜索一样,单独找大去了
费了牛鼻子劲了,终于AC
AC代码
1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 using namespace std; 5 int can_determined[101]; 6 int dir[101][101]; 7 int N,M; 8 int a,b; 9 int vis[101][101]; 10 int main() 11 { 12 // freopen("zhishu.txt","r",stdin); 13 while(cin>>N>>M){ 14 15 memset(dir,0,sizeof(dir));//如果不是多组输入则不用这句话 16 for(int i=0;i<M;i++){ 17 cin>>a>>b; 18 dir[a][b]=1; 19 }//输入数据完毕 20 21 memset(can_determined,0,sizeof(can_determined)); 22 memset(vis,0,sizeof(vis));//如果不是多组输入则不用这句话 23 for(int k=1;k<=N;k++) 24 for(int i=1;i<=N;i++) 25 for(int j=1;j<=N;j++) 26 if(vis[i][j]==0)//单独vis[i]或vis[j]都不行 27 if(dir[i][j] || (dir[i][k]==1&&dir[k][j]==1)){ 28 dir[i][j]=1;//松弛 29 vis[i][j]=1; 30 can_determined[i]++;//如果只有这句代表这仨for只能找比i小的,用例子自己想一下就知道了 31 can_determined[j]++; 32 // cout<<" "<<k<<" "<<i<<" "<<j<<" "<<can_determined[j]<<endl; 33 } 34 35 int ans=0; 36 for(int i=1;i<=N;i++) 37 if(can_determined[i]==N-1) 38 ans++; 39 cout<<ans<<endl; 40 } 41 }
这代码写的一坨屎,回去看了下“洛谷这人的题解”中的传递闭包算法思想。(但我仨for+一个for,他是仨for+俩for,不过他的传递闭包算法思想好棒)
至此这题OVER
###:电脑一直用再也没3F0放电过了
###:位运算符
###:文章里跟这个绿松色一样的三个地方,是感觉跟洛谷题解有些交集的,但是再往下没思路了。其中反存图、n次搜索、出度这仨点都跟那个搜索的题解有点像。(甚至还想过反向松弛,即4指向2,4指向3,3指向2,则直接选择最长路径,4指向3指向2,来增加数字间关系)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号