POJ1797-Heavy Transportation
继续刷邝斌飞最短路专题
垃圾POJ继续挂
每次翻译都用这个,之前一段一段帖,今儿刚发现登陆可以无限制帖然后翻译
起初以为是从N点运输给各个街道输出最大重量,但样例输出4, 可是1到2那条路是3也不行啊,难道只需要运输到各个路口?但说每条路都要走啊
难到我图画错了?百度翻译说十字路口,难道题意是三字路口之类的?
翻译理解不明白真操蛋,找题解看翻译,还要尽量避免看到解题办法
找了个题解参考博客放大300%网页,只看题意部分说:“n个点,m条带权边,求点1到点n的所有路径中最小边的最大值”
稍微想了下这咋感觉好简单呢,都跟最短路不沾边
这不跟上面的题一模一样么,买一送一啊?
撸了一坨代码出来,TLE了
想想也是,n是10^3,3层for下来就10^9
1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 #include<math.h> 5 #include<iomanip> 6 using namespace std; 7 int weight[1001][1001]; 8 int minweight[1001][1001];//minweight[1][1000]表示第1岔路口到第1000岔路口的这条街道,能承载的最小重量.短板理论 9 int main() 10 { 11 // freopen("zhishu.txt","r",stdin); 12 int t; 13 cin>>t; 14 int p=t; 15 while(t--) 16 { 17 int n,m; 18 cin>>n>>m; 19 int a,b,c; 20 memset(minweight, 0x42,sizeof(minweight)); 21 for(int i=0;i<m;i++){ 22 cin>>a>>b>>c; 23 weight[a][b]=c; 24 weight[b][a]=c; 25 minweight[a][b]=c; 26 minweight[b][a]=c; 27 } 28 29 for(int i=0;i<n;i++){ 30 weight[i][i]=0; 31 minweight[i][i]=0; 32 } 33 34 for(int k=0;k<n;k++){ 35 for(int i=0;i<n;i++) 36 for(int j=0;j<n;j++){ 37 if(minweight[i][j] < min(minweight[i][k],minweight[k][j])){ 38 minweight[i][j] = min(minweight[i][k],minweight[k][j]);//让每段的最大值最小,比如2+4和5,最大值分别为4和5,我要取2+4这条路 39 } 40 } 41 } 42 cout<<"Scenario #"<<p-t<<":"<<endl; 43 cout<<minweight[1][n]<<endl; 44 cout<<endl; 45 } 46 }
其实A的两道最短路的题后,觉得弗洛伊德算法有点懂了,但迪杰斯特拉一直只懂个算法正确性,能给不懂的人逼逼两句,但变种啥的不灵活,根本没法做题,也就是根本不算懂这个算法。上个题我就有点强迫症不甘心,但又实在不想看别人代码,md现在机会来了
依旧是上面题解说的,眼睛只看到这句“和poj2253一样,只不过那题n<=200,可以用floyd,而这题floyd会TLE,所以用dijkstra来做”
我又好开心,直接去想迪杰斯特拉算法了
人一我十人十我百
妈的又想不起来,这次不看之前的博客了,看了也忘,麻痹的直接硬想硬憋!!

昨天看山岸逢花大爆射6点才睡13:30才醒来图书馆,之前都4点睡,11:00醒。没进入学习状态之前还在骑车的时候7点睡14:00醒,15:00出门18:00到图书馆,学到23:50
怎么都不会写,感觉vis用不上啊(能确定最优解才会把这个点加入,后面改动的时候不动他),可是哪一步都确定不了最优解啊,如图
顶点1到②④⑤的承重347这仨数,哪个重量都无法确定是他们到达目的地6的短板啊,想构造的话哪个都可以为答案
感觉只能用弗洛伊德啊
想让3是答案,只需要②③和③⑥尽可能大,④⑥和⑤⑥尽可能小
想让4是答案,只需要④⑥尽可能大,②③和③⑥和⑤⑥尽可能小
想让7是答案,⑤⑥尽可能大,只需要②③和③⑥和④⑥尽可能小
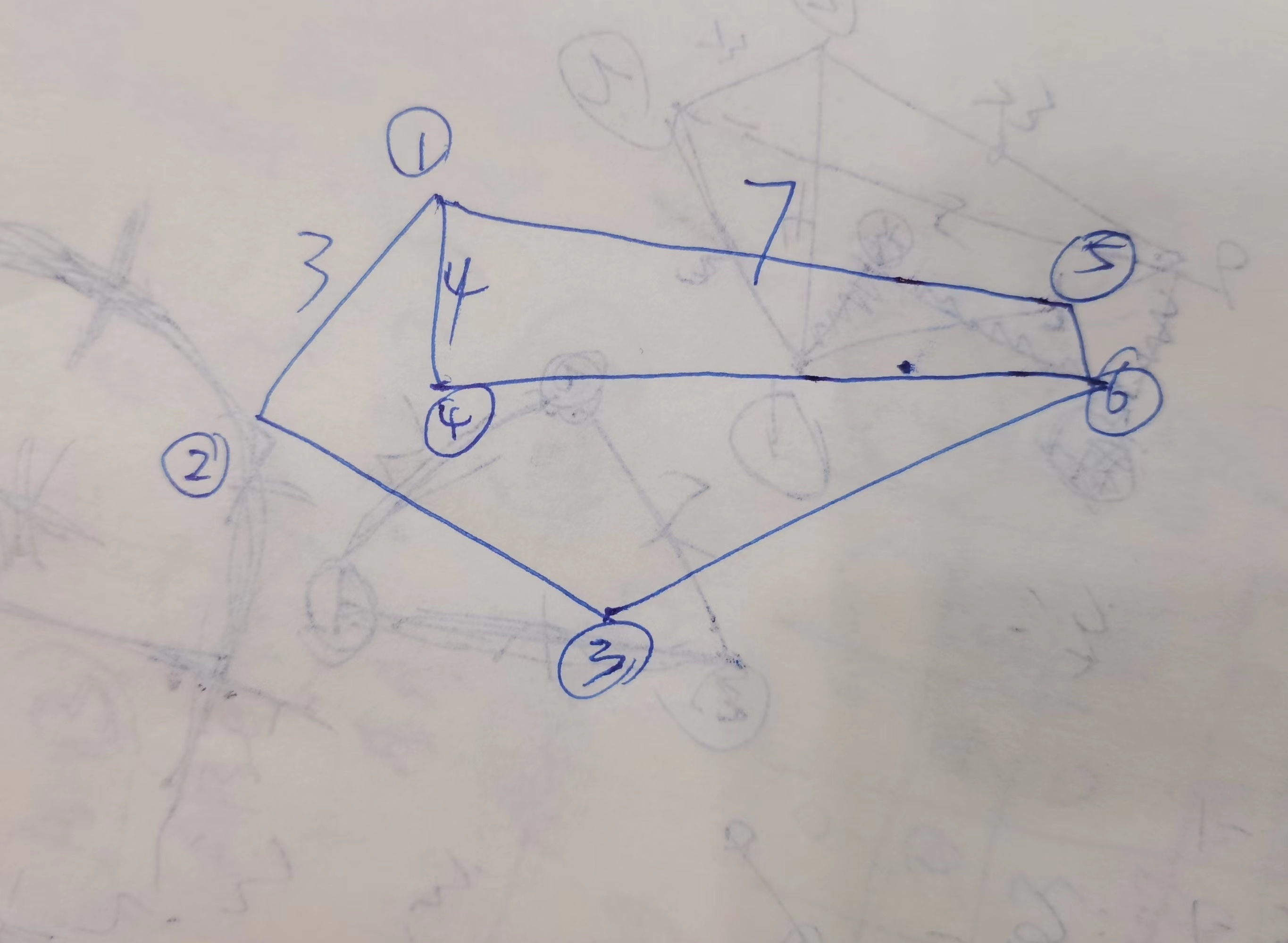
那这样的话用弗洛伊德不是更好么?咋用迪杰斯特拉啊,艹!
迪杰斯特拉思想是n步后得到最优解,
第1步找最短距离,即对于某点来说的最优解,后面咋变动,该点都不会有更优的解了,然后更新跟他沾亲带故的点
第2步在更新后的点中,找最短距离,然后更新跟他沾亲带故的点
可这题每一步都没有最优值啊,贪心个JB
看来刷题的好处就是之前博客说过,控制变量将最关键的算法本质抽丝剥茧出来,这个题,我发现了妈逼的明显每次将局部最优解加进来并不是算法本质!
我觉得之前博客学迪杰斯特拉的时候,是因为入度不方便写所以才弄的每次找最短路,入度为0时加哪个点都行!
我就瞎JB划了,写啊写(假设mindir[a]是从顶点到a点所有路径中,承载能力最弱的那条路径的,承载能力,我给他简称路径承载短板)

发现点东西,但感觉又没发现啥
换张纸再划了划了

感觉好像有点意思了,起初没啥感觉,路径和点都很少,但后面adc比的时候,推出了个公式(图片中倒数第二行),我发现如果可以把这个公式扩散到整个比较过程,问题不就解决了吗
紧接着尝试扩散公式,那起手是347仨数比较,找最大的,然后开始按照一个思路去操作:(数据用的是图里的,比如c假设为1那些,d的假设为2)
首先把①加入
找最大,7也就是⑤加入,现在不确定是否vis是否需要标记,我只是照猫画瓢,假设加入,实际这个点后面做不做更改再说,反正就是先给它拎出来
(mindir[5],c)中的最小值作为此时这条路径的短板,这个最小值能否接着用,直到最后抵达目的地,要看这个最小值跟mindir[4]和mindir[2]比咋样(这里只是为了方便表述,其实mindir[4]、mindir[2]都还没出现,应该说是dir[1][4]和dir[1][2]),如果被比如说mindir[4]干倒,那此时延伸(或者说想目的地推进)到这的时候,最牛的短板,也就是短板数据里,最能载重的一定是④这条路径,所以,我依旧是找最大,找(mindir[5],dir[5][6])的最小值、mindir[4]、mindir[2]中的最大,到这步解释清楚了,我直接写这步的总结
找最大,4也就是④加入
(mindir[4],d)中的最小值作为此时这条路径的短板,去跟mindir[2]和mindir[6]比,只是为了方便表述,但其实此时mindir[6]还没出现呢,应该说是mindir[5]和dir[5][6]中的最小值,如果d是2,c是1,那应该是②进,也就是说:(midir[4],dir[4][6])中的最小值、(mindir[5],dir[5][6])、mindir[2]这仨数中的最大值进来,到这步解释清楚了,我直接写这步的总结
找最大,3也就是②加入
(mindir[2],a)中的最小值,
(mindir[4],d)中的最小值
(mindir[5],c)中的最小值
更精准点说就是:
(mindir[2],dir[2][3])中的最小值
(mindir[4],dir[4][6])中的最小值
(mindir[5],dir[5][6])中的最小值
上面这仨找最大,作为此时的短板路径最能称重的,那反复至此执行上面操作,到⑥加入的时候,mindir[6]不就是答案了吗
至此感觉公式推出来了,再把这个公式套在上面7也就是⑤加入看行不行,那句 找(mindir[5],dir[5][6])、mindir[4]、mindir[2]中的最大 就变成了找
(mindir[5],dir[5][6])中的最小值、(mindir[1],dir[1][4])中的最小值、(mindir[1],dir[1][2])中的最小值
仨数中的最大,作为即将加入的点
这么列出来还有个好处是方便我去memset初始值,比如mindir[1]也要弄成最大(但开始写的时候发现不太对,边写边改吧)
以上是完全忘记迪杰斯特拉,才能想出来的,不然束手束脚根本想不出来,可是想出来发现,这怎么好像还是弗洛伊德呢?
不管了看看代码咋实现,边写边记录问题
1、dir其实有点歧义,名为为weight比较好
2、mindir一开始memset成最大
3、vis没啥用啊
4、实际写的时候发现好像可以不用像公式推导的那么麻烦
5、但为啥我之前看上一个题青蛙的那个,看题解迪杰斯特拉法用到了vis数组呢?整的我都不敢写了
第一次写提交WA
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 #include<iostream> 5 using namespace std; 6 int weight[1001][1001];//初始数据 7 8 int minweight[1001]; 9 //发现之前弗洛伊德TLE代码里注释表述不当,最小值tm是0啊,重新表述下:minweight[1000]表示第1岔路口到第1000岔路口的这条街道,minweight[800]表示第1岔路口到第800岔路口的这条街道,经过的路径中,承载能力最小的那条路径的承载数值.短板理论,后面让这个数值最大即所求 10 int vis[1001];//vis[2]=1表示2这个点已经加入集合,意思就是这个点判断完了,是伪最优,之后再判断的时候,从2出发看,比如图里的我2和4的vis都是1,那下次就2和4出发去弄,5没加进来vis不是1是0,那我就还1到5判断 11 int thismax; 12 int main() 13 { 14 freopen("zhishu.txt","r",stdin); 15 int t; 16 cin>>t; 17 int tp=t; 18 while(t--) 19 { 20 memset(weight,0x3f,sizeof(weight)); 21 int n,m;//n当作点,m当作边 22 cin>>n>>m; 23 memset(minweight,0x3f,sizeof(minweight)); 24 memset(vis,0,sizeof(vis)); 25 26 int a,b,c; 27 for(int i=0;i<m;i++){ 28 cin>>a>>b>>c; 29 weight[a][b]=c; 30 weight[b][a]=c;//数据输入完毕 31 } 32 33 for(int i=1;i<=n;i++) 34 minweight[i]=weight[1][i]; 35 minweight[1]=0; 36 37 int p; 38 for(int i=1;i<=n;i++){ 39 thismax=0; 40 for(int j=1;j<=n;j++){ 41 if(thismax<minweight[j]); 42 p=j; 43 } 44 // vis[p]=1; 45 for(int j=1;j<=n;j++){ 46 if(minweight[j]>min(minweight[p],weight[p][j])) 47 minweight[j]=min(minweight[p],weight[p][j]);//非常难想 48 } 49 } 50 51 cout<<"Scenario #"<<tp-t<<":"<<endl; 52 cout<<minweight[n]<<endl; 53 cout<<endl; 54 } 55 }
把我上面图里的数据测试下
1 6 7 1 2 3 1 4 4 1 5 7 5 6 1 4 6 2 2 3 5 3 6 4
妈的初始值是0x3f3f3f3f,现在要找3、4、7有数的里面无穷大,结果不0x3f3f3f3f找进来了
我要比较的只是运算过的,也就是说别人别掺乎,比如在数值7,也就是⑤加进来后,该比较3、4、和c了,那我搞个vis
这个vis搞的我写了又重构,写了又重构,反复搞好久(这块的逻辑很重要,一定自己想出来,别看别人写的,我起初试了好几种方法写)
想过把1点vis赋1,所有跟1有路径的赋1,然后比较,找出最大值的那个点标记为p,然后vis[p]=0,意思是,p已经加进来了,那下次你就别跟着比了,为啥?因为比的话找最大,应该让没进来的那些但还能从1到达的,和我p点进来后的p下面那些路去比。比如第一次⑤进来了,下一次1到5就别比了,让1到2、1到4、5到6去比,你滴明白?然后我把所有p点能到的除了1,vis都赋成2,然后把判断最大值语句改成是1就比mindir,是2就比距离,但写不下去了,这距离应该是刚出去的那个p点也就是⑤作为起点,刚加进去的那些点作为终点,看两点之间的距离,但不行啊,没法有效调出我想要的这个p点,这个点以后也要用到,这么写没法整
麻痹的后来发现还是迪杰斯特拉算法里,直接放入集合下次判断不考虑他的写法是对的,不用特意判断两点距离,因为后面的松弛操作已经记录到mindir里了
一下子豁然开朗了
发现上面WA里的松弛那个比较写反了,命名也很容易误导,应该叫maxdir,但对上面讲的没影响
妈的导致memset也搞反了。然后比较大小那也没重新给thismax赋值,这里初始值真他妈不好想啊!!!
改完AC了
AC代码
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 #include<iostream> 5 using namespace std; 6 int weight[1001][1001];//初始数据 7 8 int maxweight[1001]; 9 //发现之前弗洛伊德TLE代码里注释表述不当,最小值tm是0啊,重新表述下:maxweight[1000]表示第1岔路口到第1000岔路口的这条街道,maxweight[800]表示第1岔路口到第800岔路口的这条街道,经过的路径中,承载能力最小的那条路径的承载数值.短板理论,后面让这个数值最大即所求 10 int vis[1001];//vis[2]=1表示2这个点已经加入集合,意思就是这个点判断完了,是伪最优,之后再判断的时候,从2出发看,比如图里的我2和4的vis都是1,那下次就2和4出发去弄,5没加进来vis不是1是0,那我就还1到5判断 11 int thismax; 12 int main() 13 { 14 // freopen("zhishu.txt","r",stdin); 15 int t; 16 cin>>t; 17 int tp=t; 18 while(t--) 19 { 20 memset(weight,0x3f,sizeof(weight));//没路是0,或者无穷大都行,0也可以AC 21 int n,m;//n当作点,m当作边 22 cin>>n>>m; 23 memset(maxweight,0,sizeof(maxweight)); 24 memset(vis,0,sizeof(vis)); 25 26 int a,b,c; 27 for(int i=0;i<m;i++){ 28 cin>>a>>b>>c; 29 weight[a][b]=c; 30 weight[b][a]=c;//数据输入完毕 31 } 32 for(int i=1;i<=n;i++) 33 weight[i][i]=0; 34 35 for(int i=1;i<=n;i++) 36 if(weight[1][i]!=0x3f3f3f3f) 37 maxweight[i]=weight[1][i];//1到自身都是0,其他有路都是具体数值 38 int p; 39 //vis[1]用不到 40 for(int i=1;i<=n;i++){ 41 thismax=0; 42 for(int j=1;j<=n;j++){ 43 if(thismax<maxweight[j]&&vis[j]==0){ 44 p=j; 45 thismax=maxweight[j]; 46 } 47 } 48 vis[p]=1; 49 //cout<<"!"<<p<<" "<<vis[p]<<" $"<<vis[2]<<endl; 50 for(int j=2;j<=n;j++){//松弛 51 if(weight[p][j]!=0x3f3f3f3f)//确定是沾亲带故,否则这段没有路,min就是0x3f3f3f3f,那不考虑是不是沾亲带故,就把这个没路的给整成有路了,沾亲带故其实就是从这个点出发,有路可以走的.原算法是相加,无穷大依旧是无穷大,但这里是比较,会将没路的更新成某个数值 52 if(maxweight[j]<min(maxweight[p],weight[p][j])){ 53 maxweight[j]=min(maxweight[p],weight[p][j]); 54 } 55 // cout<<"#######"<<maxweight[j]<<endl; 56 } 57 } 58 59 cout<<"Scenario #"<<tp-t<<":"<<endl; 60 cout<<maxweight[n]<<endl; 61 cout<<endl; 62 } 63 }
另一种AC写法(全0写法)
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 #include<iostream> 5 using namespace std; 6 int weight[1001][1001]; 7 int maxweight[1001]; 8 int vis[1001]; 9 int thismax; 10 int main() 11 { 12 // freopen("zhishu.txt","r",stdin); 13 int t; 14 cin>>t; 15 int tp=t; 16 while(t--) 17 { 18 // memset(weight,0x3f,sizeof(weight));//没路是0,或者无穷大都行 19 memset(weight,0,sizeof(weight));//没路是0,或者无穷大都行,上面那行也AC 20 int n,m; 21 cin>>n>>m; 22 memset(maxweight,0,sizeof(maxweight)); 23 memset(vis,0,sizeof(vis)); 24 25 int a,b,c; 26 for(int i=0;i<m;i++){ 27 cin>>a>>b>>c; 28 weight[a][b]=c; 29 weight[b][a]=c;//数据输入完毕 30 } 31 for(int i=1;i<=n;i++) 32 weight[i][i]=0; 33 34 for(int i=1;i<=n;i++) 35 // if(weight[1][i]!=0x3f3f3f3f) 36 maxweight[i]=weight[1][i];//1到自身都是0,其他有路都是具体数值 37 int p; 38 for(int i=1;i<=n;i++){ 39 thismax=0; 40 for(int j=1;j<=n;j++){ 41 if(thismax<maxweight[j]&&vis[j]==0){ 42 p=j; 43 thismax=maxweight[j]; 44 } 45 } 46 vis[p]=1; 47 for(int j=2;j<=n;j++){//松弛 48 // if(weight[p][j]!=0x3f3f3f3f)//确定是沾亲带故,否则这段没有路,min就是0x3f3f3f3f,那不考虑是不是沾亲带故,就把这个没路的给整成有路了,沾亲带故其实就是从这个点出发,有路可以走的.原算法是相加,无穷大依旧是无穷大,但这里是比较,会将没路的更新成某个数值 49 if(maxweight[j]<min(maxweight[p],weight[p][j])){ 50 maxweight[j]=min(maxweight[p],weight[p][j]); 51 } 52 } 53 } 54 cout<<"Scenario #"<<tp-t<<":"<<endl; 55 cout<<maxweight[n]<<endl; 56 cout<<endl; 57 } 58 }
又另一种AC写法
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 #include<iostream> 5 using namespace std; 6 int weight[1001][1001]; 7 int maxweight[1001]; 8 int vis[1001]; 9 int thismax; 10 int main() 11 { 12 // freopen("zhishu.txt","r",stdin); 13 int t; 14 cin>>t; 15 int tp=t; 16 while(t--) 17 { 18 // memset(weight,0x3f,sizeof(weight));//没路是0,或者无穷大都行 19 memset(weight,0,sizeof(weight));//没路是0,或者无穷大都行,上面那行也AC 20 int n,m; 21 cin>>n>>m; 22 memset(maxweight,0,sizeof(maxweight)); 23 memset(vis,0,sizeof(vis)); 24 25 int a,b,c; 26 for(int i=0;i<m;i++){ 27 cin>>a>>b>>c; 28 weight[a][b]=c; 29 weight[b][a]=c;//数据输入完毕 30 } 31 for(int i=1;i<=n;i++) 32 weight[i][i]=0; 33 weight[1][1]=0x3f3f3f3f; 34 for(int i=1;i<=n;i++) 35 // if(weight[1][i]!=0x3f3f3f3f) 36 maxweight[i]=weight[1][i];//1到自身是0,其他有路都是具体数值,没路是无穷大 37 int p; 38 for(int i=1;i<=n;i++){ 39 thismax=0; 40 for(int j=1;j<=n;j++){ 41 if(thismax<maxweight[j]&&vis[j]==0){ 42 p=j; 43 thismax=maxweight[j]; 44 } 45 } 46 vis[p]=1; 47 for(int j=1;j<=n;j++){//松弛 48 // if(weight[p][j]!=0x3f3f3f3f)//确定是沾亲带故,否则这段没有路,min就是0x3f3f3f3f,那不考虑是不是沾亲带故,就把这个没路的给整成有路了,沾亲带故其实就是从这个点出发,有路可以走的.原算法是相加,无穷大依旧是无穷大,但这里是比较,会将没路的更新成某个数值 49 if(maxweight[j]<min(maxweight[p],weight[p][j])){//没有路就是0,min函数中比较,对于没路的点,一定是0胜出,0不可能大于任何数,所以这一步相当于间接筛掉了那些不是沾亲带故的 50 maxweight[j]=min(maxweight[p],weight[p][j]); 51 } 52 } 53 } 54 cout<<"Scenario #"<<tp-t<<":"<<endl; 55 cout<<maxweight[n]<<endl; 56 cout<<endl; 57 } 58 }
说下思路(win+←开俩标签也看,对比上面那个图)
首先找①点到能到达的里面最大的,是7,找出后,⑤点选出来了,做跟他沾亲带故的松弛,松弛完该干啥了?
显然是比较①②、①④、⑤⑥仨数(3、4、1)谁大啊,更确切的来说,不是⑤⑥而是刚加进来的⑤点沾亲带故更新后①⑤和⑤⑥之间的短板称重
发现①④最大,但这个最大代码怎么写,理论上来说是要有⑤⑥承重数据参与的,因为他是①⑤和⑤⑥的min嘛,但问题来了,循环内你咋去找这个起点⑤,如果很多步之后有很多个这种非①点作为起始的两点称重数据段参与比较,起点你咋找?于是我发现其实在松弛的时候这个⑤⑥称重就已经当作短板记录到了minweight[6]当中,即minweight[6]是1,那我是不是直接for遍历整个点就行了?即①到②③④⑤⑥最大,但注意①到⑤还用掺乎进来比了吗,显然他再大都已经没用了,已经有了⑤⑥作为短板承重了,到这豁然开朗,设置个vis,⑤进来过就赋值为1,下次别进来跟着比了,目前也就更加了解迪杰斯特拉算法本质,每次找的局部最优,在原始算法中亦是全局最优,也就是说,到某点的,此时的,最短距离,那该点加进来后,一直到最后也是顶点到该点最短的,但此题又发现,每次加进来的比如第一次⑤加进来,但最后①⑥短板承重答案是3,即①②③⑥,跟⑤没关系,⑤只是伪最优,是向真最优答案方向发展了,无数个伪最优中,到尽头,一定是真最优,叙述到这,一些词汇跟我最开始博客里的一些话就对上了,所以没有这个推导过程,直接看我这个总结结论就是一堆天数屁话根本看不懂,所以还得自己亲自推导啊。然后,虽然说⑤加进来之后不再加进来了,且⑤走完就到⑥了,但没关系,后面其他点进入会使得⑤或者⑥更能承重,则松弛
再说代码里的想了我好久的memset问题,我想到了三种写法:(代码里的注释可能是乱的,看下面的就行)
“另一种AC写法(全0写法)”
maxweight:①到某点的承重赋上初始给定的值,其他memset为0
至于weight,一开始memset全0,俩俩之间有路径的的赋值为具体距路径承重
然后重点来了,比较的时候,两点之间没有路,即不是刚刚加入的沾亲带故的点(加入的点用p标记了),就是0,min函数中比较,对于没路的点, min(maxweight[p],weight[p][j]) 这句话一定返回的是weight[p][j]的值,也就是没路的,也就是0,0不可能大于任何数,所以这一步相当于间接筛掉了那些不是沾亲带故的
如果是遍历的加入的点,也即是自身的话,⑤加进来,7<min(7,0)不成立,不会松弛,至此结束
再来说说最开始那个“AC代码”
maxweight,①到该点有路就赋具体值,1到1是0,没路也是0
weight,有路的赋具体数值,自身到自身是0,没路是0x3f3f3f3f无穷大
然后重点来了,比较的时候要加上一句 if(weight[p][j]!=0x3f3f3f3f) ,没路的就别松弛了,会出错,比如我下面这个图

如果轮到④加进去,假设使得maxweight[5]是3,遍历如果遍历到没路的⑦这个点,比较后就就会进行松弛。我起初以为小数2不可能在大数3之前加进去,后来明白了这是遍历不是找最大那个操作
注意:上面两个代码都是从2开始松弛的,试想一下,如果是从1开始,1到1是0,松弛的时候,如果⑤加进来,松弛到1,0 < min(7,7)成立,就会把1到自身给错误地松弛掉。这也就有了
“又另一种AC写法”
将1到1的承重初试设为无限大就没事了,即 weight[1][1]=0x3f3f3f3f;
但我写到这突然又发现个事,如果maxweight[1]设无限大,第一次进入的就是1点,那我松弛的时候,就可以进行类似于起初初始化赋值操作,所以起初赋值那也省了。更新最简洁代码
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 #include<iostream> 5 using namespace std; 6 int weight[1001][1001]; 7 int maxweight[1001]; 8 int vis[1001]; 9 int thismax; 10 int main() 11 { 12 // freopen("zhishu.txt","r",stdin); 13 int t; 14 cin>>t; 15 int tp=t; 16 while(t--) 17 { 18 memset(weight,0,sizeof(weight)); 19 int n,m; 20 cin>>n>>m; 21 memset(maxweight,0,sizeof(maxweight)); 22 memset(vis,0,sizeof(vis)); 23 24 int a,b,c; 25 for(int i=0;i<m;i++){ 26 cin>>a>>b>>c; 27 weight[a][b]=c; 28 weight[b][a]=c;//数据输入完毕 29 } 30 for(int i=1;i<=n;i++) 31 weight[i][i]=0; 32 maxweight[1]=0x3f3f3f3f; 33 // for(int i=1;i<=n;i++) 34 // maxweight[i]=weight[1][i]; 35 int p; 36 for(int i=1;i<=n;i++){ 37 thismax=0; 38 for(int j=1;j<=n;j++){//找最大 39 if(thismax<maxweight[j]&&vis[j]==0){ 40 p=j; 41 thismax=maxweight[j]; 42 } 43 } 44 vis[p]=1; 45 for(int j=1;j<=n;j++){//松弛 46 if(maxweight[j]<min(maxweight[p],weight[p][j])){ 47 maxweight[j]=min(maxweight[p],weight[p][j]); 48 49 } 50 } 51 } 52 cout<<"Scenario #"<<tp-t<<":"<<endl; 53 cout<<maxweight[n]<<endl; 54 cout<<endl; 55 } 56 }
艹!兜兜转转发现就是之前最原始的算法的写法,但只有这样自己趟过一遍才能更了解算法思想
至此OK
看看别人代码咋写的
大部分用了队列,妈的我发现我代码是最朴素的,就跟原始人似得,其他人都用了点高科技,比如pair,map啥的,等刷完邝斌飞开始学C++再弄那些吧
有说最大生成树的(邝斌有这个专题,不管了,后面再说),随手放俩感觉还不错的博客、参考博客
他们博客里写的都更专业,但不接地气,不知道思路的根本看不懂,什么状态转移方程,队列取最大,我只能一个一个核对最后发现是一样的,但对不知道咋解题的很不友好,没有桥梁衔接
更新:刷后面Wormholes的时候,发现POJ好了,把之前的代码交下发现,cin会超时,改后POJ也能AC的代码如下
AC代码
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 #include<iostream> 5 using namespace std; 6 int weight[1001][1001];//初始数据 7 8 int maxweight[1001]; 9 //发现之前弗洛伊德TLE代码里注释表述不当,最小值tm是0啊,重新表述下:maxweight[1000]表示第1岔路口到第1000岔路口的这条街道,maxweight[800]表示第1岔路口到第800岔路口的这条街道,经过的路径中,承载能力最小的那条路径的承载数值.短板理论,后面让这个数值最大即所求 10 int vis[1001];//vis[2]=1表示2这个点已经加入集合,意思就是这个点判断完了,是伪最优,之后再判断的时候,从2出发看,比如图里的我2和4的vis都是1,那下次就2和4出发去弄,5没加进来vis不是1是0,那我就还1到5判断 11 int thismax; 12 int main() 13 { 14 // freopen("zhishu.txt","r",stdin); 15 int t; 16 scanf("%d",&t); 17 int tp=t; 18 while(t--) 19 { 20 memset(weight,0x3f,sizeof(weight));//没路是0,或者无穷大都行,0也可以AC 21 int n,m;//n当作点,m当作边 22 scanf("%d%d",&n,&m); 23 memset(maxweight,0,sizeof(maxweight)); 24 memset(vis,0,sizeof(vis)); 25 26 int a,b,c; 27 for(int i=0;i<m;i++){ 28 scanf("%d%d%d",&a,&b,&c); 29 weight[a][b]=c; 30 weight[b][a]=c;//数据输入完毕 31 } 32 for(int i=1;i<=n;i++) 33 weight[i][i]=0; 34 35 for(int i=1;i<=n;i++) 36 if(weight[1][i]!=0x3f3f3f3f) 37 maxweight[i]=weight[1][i];//1到自身都是0,其他有路都是具体数值 38 int p; 39 //vis[1]用不到 40 for(int i=1;i<=n;i++){ 41 thismax=0; 42 for(int j=1;j<=n;j++){ 43 if(thismax<maxweight[j]&&vis[j]==0){ 44 p=j; 45 thismax=maxweight[j]; 46 } 47 } 48 vis[p]=1; 49 //cout<<"!"<<p<<" "<<vis[p]<<" $"<<vis[2]<<endl; 50 for(int j=2;j<=n;j++){//松弛 51 if(weight[p][j]!=0x3f3f3f3f)//确定是沾亲带故,否则这段没有路,min就是0x3f3f3f3f,那不考虑是不是沾亲带故,就把这个没路的给整成有路了,沾亲带故其实就是从这个点出发,有路可以走的.原算法是相加,无穷大依旧是无穷大,但这里是比较,会将没路的更新成某个数值 52 if(maxweight[j]<min(maxweight[p],weight[p][j])){ 53 maxweight[j]=min(maxweight[p],weight[p][j]); 54 } 55 // cout<<"#######"<<maxweight[j]<<endl; 56 } 57 } 58 59 cout<<"Scenario #"<<tp-t<<":"<<endl; 60 cout<<maxweight[n]<<endl; 61 cout<<endl; 62 } 63 }
###:总结下弗洛伊德算法就是,加点,然后大遍历,点咋加都行但必须每个点都加一遍,大遍历的时候也是咋遍历都行,但必须全部遍历到
###:题意其实就是有个巨轮推土机,要从1去往n,基于根据短板理论,找最牛逼的最能承重的路径
###:代码有思路不知道咋写最好的办法就是硬憋
学习新算法不知道怎么实现,最好的办法就是可以先看一遍代码,然后记住算法原理,忘记看的代码,硬憋,一点都不要有之前代码的痕迹记忆。如果你有思路但写不出来代码,这时候照着代码抄一遍,基本就完犊子了,脑瓜子里存了一堆挥之不去的脏数据。那些代码博客是自己A了好多题后水平高了才能看懂了
如果知道啥算法没思路,也硬憋,看题解基本一点用处没有,请教过山理首金金泽巨说把握看题解的时间,想1h,但我是想超过2天才看题解,毕竟我思路慢,但这样逐渐就会像惊蛰雨一样,1h就可以看题解了。主要是要做到1h内把所有可能都想到都没其他办法了才行。不然永远是看题解然后心中:“确实,是这么回事”,但毫无长进,到区域赛赛场上只能说足无措的坐在那看别人挂气球,读题翻译想思路+写代码+找bug,就成了读题翻译写代码找bug都一个人,你在那擦键盘喂面包端茶倒水。美赛3天(英语专业写论文+做实验数据+翻译,你在那呆呆的无所事事)
###恍惚之间总用弗洛伊德的思想去想迪杰斯特拉
###:我是顺序思路进行写的博客,很多人想完直接写结论,导致根本看不懂,有时候别人的博客要倒着看
###:今W钰H兄弟主动找我,害十一来玩的时候就想给他买点坚果,但没工作进度又慢的要死,没脸见,还是找到工作再联系他吧
###:一星期后回来看自己博客,发现都不愿意看




 浙公网安备 33010602011771号
浙公网安备 33010602011771号