POJ1426-Find The Multiple
简单回一下类型的最大长度,参考博客、参考博客,(感觉都写的乱七八糟都不太一样又都不全)发现数学运算是不行了,题目最多100位呢
同样题目其他平台、洛谷OJ,(防止垃圾POJ再次崩,且如果这两个平台是自己的数据的话,要比poj数据强,但有时候题目直接拉poj数据过去就不行了)
先简单回顾下浮点型知识
回忆起DevC++编译器
这博客里的“%Le”也不对啊,

1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 int main() 5 { 6 7 long double bug=5.34e-7;//这Le输出了个啥!! 8 printf("%Lf or %Le\n", bug, bug); 9 long double i=1001001001001001.0/6; 10 printf("%Lf or %Le\n",i,i);//Lf Le都不对,且Le输出很诡异 11 __mingw_printf("%Lf or %Le\n",i,i);//Lf Le也必须加__mingw,L必须大写_ 12 __mingw_printf("%Lf\n", i);//必须大写,且double用mingw会卡死 13 cout << i<<endl; 14 15 printf("\n"); 16 printf("\n"); 17 18 double a=100100100100100100.0/6; 19 printf("%Lf or %lf or %llf or %f\n",a, a,a,a); 20 printf("%e %le %Le\n",a,a,a); 21 cout << a<<endl; 22 }
唯一对的博客
综上,要么cout永远不会错,要么用printf:
在double时候用 %f、%lf、%llf、%Lf 哪个都可以,如果科学计数法表示就 %e %le %Le 哪个都行。
long double的时候涉及到的printf必须用 __mingw_printf ,用 %Lf 输出且Lf大写,如果科学计数法就 %Le 输出且Le大写
但注意,如果double用 __mingw_printf ,程序就会卡死
补基础知识
好了前面知识基本回顾完了
西安算法竞赛培训WYH给我讲有趣的事,亚洲区域赛冠军比季军多A一个题,就是把一个超时的题目,把超时的部分打表,得了冠军,应该是上交or清华的事
我直接暴力打200个表哈哈AC后玩玩
回忆区域赛网络赛魔方问题,总共就8个可能,yes/no,有个学校暴力提交测评网站直接炸了
其他都不说,就单单验证为什么111...11是19的倍数就想不出来了。
这里肯定不能用运算,因为最大有100位,而运算数值类型最大也就是long long不超过20位
实在想不出,看了下题解,把网页调成300%,遮挡下面的行,尽量略过不去看思路解析,简单读了下这个文章,我靠???怎么直接运算了,最后发现样例给定不是最小的,运行了文章里代码发现6最小的答案不是100100100100100100,惊呆了,因为看到19都有这么多位数了,那200不得更大,且说位数最大100位直接绕过运算操作想了一天,我以为是用字符串怎么搜。诸如用什么搜索出6的倍数还不能用乘除取模运算,然后一位一位看是不是只有01,或者对于6来说,从10开始11,100,101,110,111这样往下搜,看哪个是6的倍数但也绕不过运算。好家伙还把计算器调成程序员(发现这是整型),调成科学,验证111111111111111111除以19得几
其实很好奇为啥要弄个这么个样例
这下知道不超类型后想看看最大是多少,样例范围是200,先试一下199
写了如下代码

1 #include<stdio.h> 2 int main() 3 { 4 5 6 for(int i=1;i<1000000;i++){ 7 long ans=199*i; 8 while(ans%10==0||ans%10==1 &&(ans!=0&&ans!=1)) 9 ans=ans/10; 10 if(ans==1||ans==0) 11 printf("$$%d\n",199*i); 12 } 13 14 }
期间遇到小坑点
###: while(0.1)//一样死循环 printf("#");
###:double不允许取模,比如定义 long double ans=199; 如果ans跟个 ans%10; 就会报错: error: invalid operands of types 'long double' and 'int' to binary 'operato
###:强制转化要加括号
###:不小心写成 scanf("%d\n",&a); 输入6回车,再输入个东西才行。如果 scanf("\n%d",&a); 是正常的。输入
随后写了个代码
1 #include<stdio.h> 2 int main() 3 { 4 int a; 5 while(scanf("%d",&a) && a!=0){ 6 for(int i=1;i<1000000000;i++){ 7 long ans=a*i; 8 while(ans%10==0||ans%10==1 &&(ans!=0&&ans!=1)) 9 ans=ans/10; 10 if(ans==1||ans==0){ 11 printf("%d\n",a*i); 12 break; 13 } 14 } 15 } 16 }
发现199很快输出了,9输出很慢,是9*12345679=111111111,而99都啥也不输出,
博客关于long 各种类型写的乱七八糟懒得管这个,有些博客还没有long,只有long int,先直接瞎鸡巴往后填0不管范围,范围等AC后再来收拾你,先搁置
加了几个0,long long输出是lld还是啥先不管

1 #include<stdio.h> 2 int main() 3 { 4 int a; 5 while(scanf("%d",&a) && a!=0){ 6 for(long long i=1;i<100000000000000000000;i++){ 7 long long ans=a*i; 8 while(ans%10==0||ans%10==1 &&(ans!=0&&ans!=1)) 9 ans=ans/10; 10 if(ans==1||ans==0){ 11 printf("%lld %lld\n",i,a*i); 12 break; 13 } 14 } 15 } 16 }
long long输出

1 #include<stdio.h> 2 int main() 3 { 4 long a=2147483647; 5 printf("%d\n",a);//都可以 6 printf("%lld\n",a);//都可以 7 8 long long b=234147483647; 9 printf("%d\n",b); 10 printf("%ld %Ld\n",b,b); 11 printf("%lld\n",b);//只有这个可以 12 13 long long int q=1111111111111111110; 14 printf("%d %lld\n",q, q);//lld才行 15 16 }

好想把牛子赛道左边维族妹子女士嘴里
男人脏,女人味大傻了吧唧,但73聪明,就是一群下贱牲口,但身材狗骚,歌姬舞姬天生适合做妓女,做妓女就很很高贵没风俗起激发起欲望
运行99我tm等了一年都没有结果,测试发现光一个空的for循环,10^8是0.3s,10^9是3s,我电脑是hp envy13,发现13个0就已经咋等都不输出了(程序只有一个for)。
###:发现%d输出的488441933*99是1111111111,%lld是48355751367,期间程序99输出11..11导致的错误
###:运行了下AC代码,就是上面提到的文章,发现99*1122334455667789=111111111111111111。这里99乘了个16位的数才是答案,但从1遍历到13位就已经不输出东西了
###:冥思苦想,迷宫是上下左右一定会搜完全部,那这个咋搜?往深搜上靠,dfs到顶部再回来啥啥的。觉得可以比如99,初始化成100(6就是初始化成10),%是0就加1→101,%是1倒数第二位是0就倒数第二位加1后面全变0→110,→111,全是1就1000,→1001→.....→10111,到数第四位变1,后面全0,看上面提到的文章里,扫到说是取模搜索,%10,但思路还是没有,基本等于没看,就挺好,继续自己想,发现这个过程没法用代码写出来,回去路上又想怎么跟迷宫搜索结合起来,

到家想了会,又上tg撸管子去了了,哎好烦这样的自己,欲望强烈我有什么办法
没思路好像看题解啊啊啊啊啊,第二天去图书馆就想怎么实现,基本重复的内容写了一块纸又一块纸,最后发现有点思路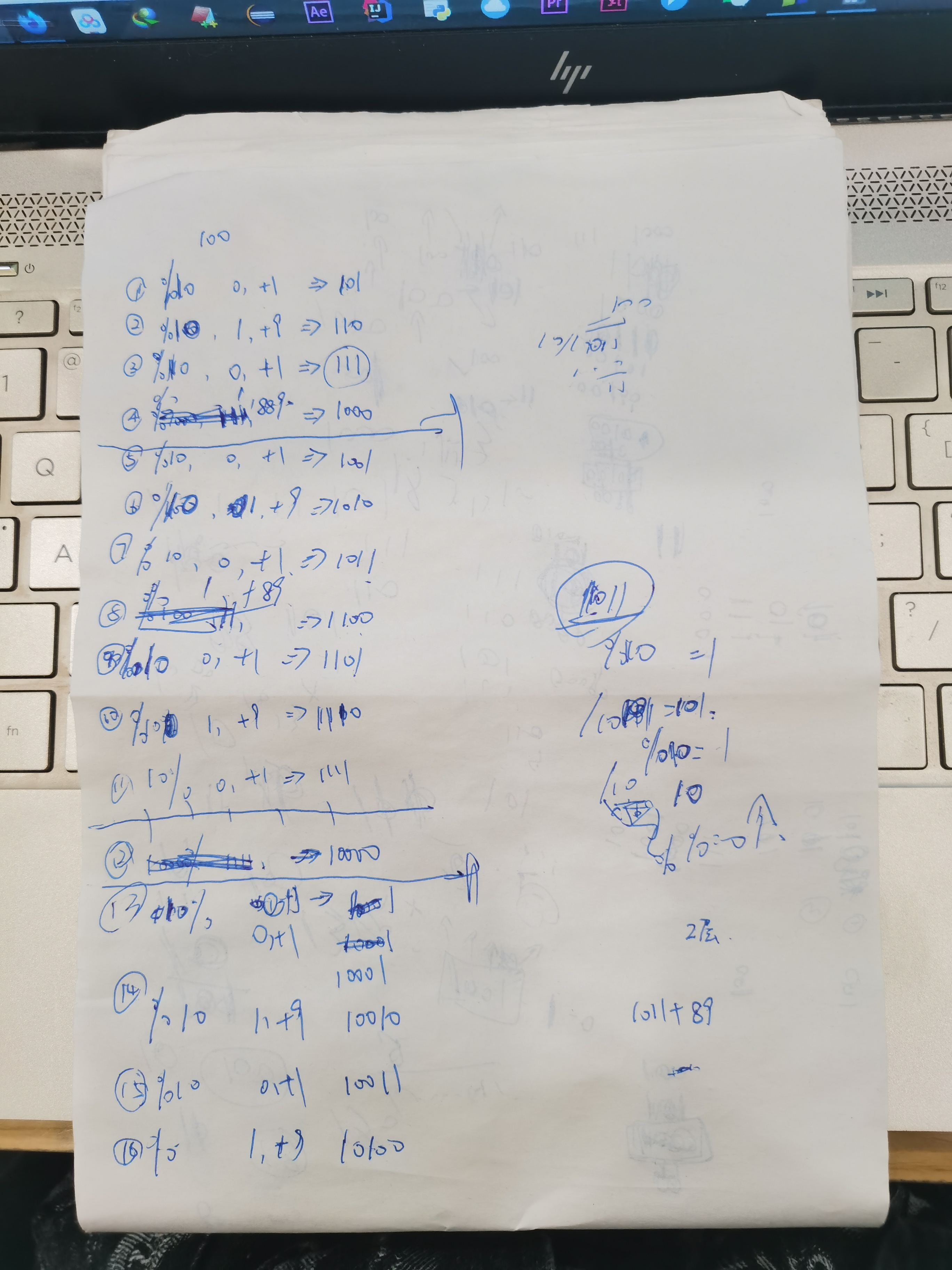
期间反复改,发现有个统一的规律,是0就+1,是1就进入层数递归,比如右边例子,1011,
%10是1,进入递归记录1层,/10,→101,
%10是1,进入递归记录2层,/10,→10
%10是0,好停,记录了2层那么,就是8*(2-1)的十次幂 + 9
多写几个就知道了
###:遇到的坑:回顾之前博客,“一个变量进行递归的时候”,即局部变量、全局变量、函数参数在递归函数里return后值的变化。
这里再加一个函数参数

1 #include<stdio.h> 2 int N; 3 void fn(int x) 4 { 5 if(x == 2){ 6 x++; 7 printf("#%d\n", x); 8 return; 9 10 } 11 else 12 { 13 fn(x + 1); 14 printf("%d\n", x); 15 } 16 } 17 int main() 18 { 19 scanf("%d", &N);//1 20 fn(N); 21 }
输入1输出#3和1,发现进入下一层递归函数后,再返回来后,参数是不变的。(很重要的东西)
但函数的参数,在函数内改变是会随着改变的

1 #include<stdio.h> 2 int N; 3 void fn(int x) 4 { 5 x=5; 6 printf("%d\n", x); 7 8 } 9 int main() 10 { 11 scanf("%d", &N);//1 12 fn(N); 13 printf("%d\n", N); 14 }
这些坑坑洼洼的小知识之前从没意识到过
###:又回顾了下之前博客,return在while里的作用
###:chrome总闪退,懒得找原因,勤快点Ctrl+s
西安算竞培训艾教V8重新设计有几个函数内的变量,有几个全局变量来作为中间存储变量,搜索逻辑
推翻重写好几遍,真的好难啊这题。感觉思维好迟钝~~~~(>_<)~~~~
感觉代码写的好乱思路跟打补丁一样,但想起V8说只要有思路就写别管多么离谱

高中数学老师,你可以说我挫,但不可以侮辱我家人,美国流浪汉,说美国已经完了,80%的人都没有同情心。那时候还没这么对立,以后只要班里有一个人记得我说过的话我就知足了
###:回顾之前博客,i++/++i
不仅printf如此,pow函数也如此,递归也是如此(之前都是把++放在函数外面的,所以没踩过这个坑)

1 #include<stdio.h> 2 #include<math.h> 3 void f(int a) 4 { 5 if(a==2) 6 { 7 printf("%d\n",a); 8 return; 9 } 10 if(a==1) 11 // f(++a);//输出2 #2 12 // f(a++);//超时返回异常,因为始终都不会正常结束 13 f(a+1);//输出2 #1 14 printf("#%d\n",a); 15 } 16 int main() 17 { 18 int a=1; 19 double b=pow(3,++a); 20 int c=b; 21 printf("%lf\n",b);//输出9.000000 22 printf("%d\n",c);//输出9 23 24 f(1); 25 }
个人觉得递归还是用+1比较好,这样再回来还能是这个参数

1 #include<stdio.h> 2 int f(int i) 3 { 4 if(i==1) 5 { 6 f(i+1);//f(i++); 7 printf("%d\n",i); 8 } 9 if(i==2) 10 printf("#\n"); 11 } 12 int main() 13 { 14 f(1); 15 }
思路:
101 dfs 10 1 dfs 发现n&10==0,return 1011 0 dfs 101 1 dfs 10 2 dfs 发现n%10==0,return 回到dfs 10 2 此时赋值8*10^..,但若到了第一层即个位,则p赋值为9,return 回到dfs 101 1 11 dfs 1 1 dfs 0 2 dfs发现0%10==0,return 回到dfs 0 2 p=80 return 回到dfs 1 1 p=89 return
按照这个写发现写不下去了,设计的搜索逻辑
1 //thisn代码是写完下面的再加的,所以顺序看看懂跟实际能写AC两码事 2 //总想总结,因为总觉得以后再也想不出来A不了了 3 #include<stdio.h> 4 #include<iostream> 5 using namespace std; 6 #include<math.h> 7 void dfs(int n,int storey); 8 int num;//最初输入 9 int nok;//真正的用于存储输入值num的 10 int flag;//初始化标记,记录输入值num有多少位 11 int n;//初始化后存于此 12 int p=0;//dfs搜索后仅包含0和1的结果 13 int main() 14 { 15 while(scanf("%d",&num)&&num){ 16 nok=num; 17 flag=1; 18 while(num/10){ 19 num=num/10; 20 flag++; 21 } 22 n=pow(10,flag); 23 dfs(n,0); 24 } 25 } 26 27 void dfs(int n, int storey) 28 { 29 if(n%10==0&&storey==0){ 30 if(n%nok==0){ 31 printf("%d\n",n); 32 return; 33 } 34 else 35 n=n+1; 36 } 37 if(n%10==0&&storey!=0) 38 return; 39 if((n%10==1)){ 40 storey++; 41 printf("#%d %d\n",n/10,storey); 42 dfs(n/10,storey); 43 printf("@%d %d\n",n/10,storey); 44 if(storey==1){ 45 p=n+p+9; 46 printf("****%d\n",p); 47 if(p%nok==0){ 48 printf("%d\n",p); 49 return; 50 } 51 } 52 if(storey!=1){ 53 p=p+8*pow(10,--storey); 54 printf("!!%d\n",p); 55 return; 56 } 57 } 58 }
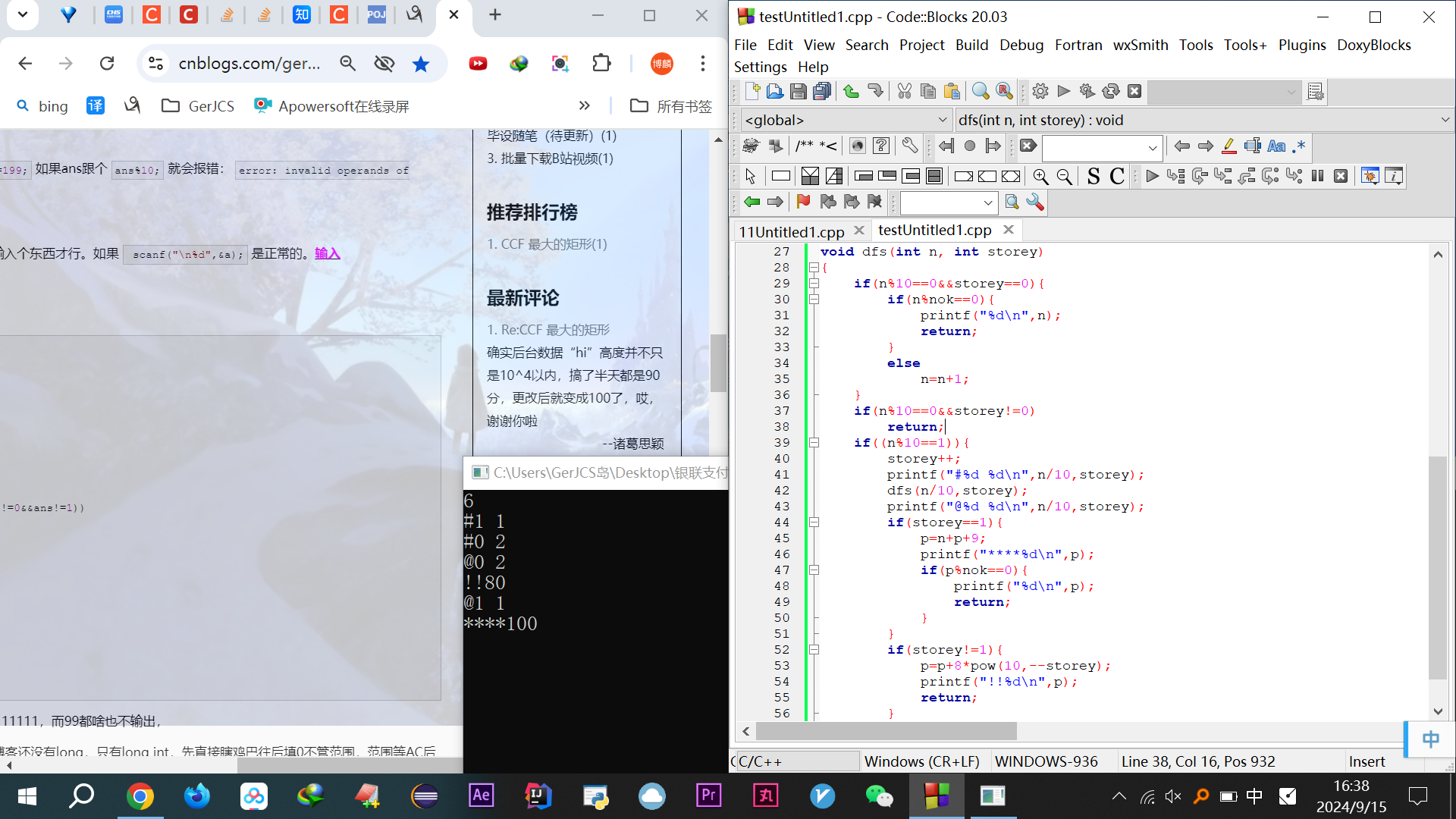

这个评论,我自己估计都看不懂之前代码,这诸葛思颖居然能看懂
输入6,初始化为10,+1,→11,然后+89→100,但这往下应该再+1,如果递归,归回来我还得用到上面这些呢,加8..89,乱套了。
思考:不重复进去啊递归只是给自己用的,没格局到宏观路径啊,有没有可能用while那个广搜,或者像棋盘问题搜有几个1,好像也都不行。(有没有可能写两遍dfs,感觉不太可能。后来发现确实是用两次dfs)
不看题解再挣扎一下,迷宫有返回,这个一直增大+1,或者加8..89,试试while
总算写出个有点样子的

1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #include<math.h> 5 int dfs(int n,int storey); 6 int num;//最初输入 7 int nok;//真正的用于存储输入值num的 8 int flag;//初始化标记,记录输入值num有多少位 9 int n;//初始化后存于此 10 int p;//dfs搜索后仅包含0和1的结果 11 12 int isfind; 13 int main() 14 { 15 while(scanf("%d",&num)&&num){ 16 isfind=0; 17 nok=num; 18 flag=1; 19 while(num/10){ 20 num=num/10; 21 flag++; 22 } 23 n=pow(10,flag); 24 while(isfind==0) 25 { 26 p=0; 27 if(n%10==0) 28 n++; 29 if(n%10==1){ 30 n=dfs(n,0); 31 if(n%nok==0){ 32 printf("%d\n",n); 33 isfind=1; 34 } 35 } 36 } 37 } 38 } 39 int dfs(int n, int storey) 40 { 41 42 if(n%10==0&&storey!=0) 43 ; 44 45 if((n%10==1)){ 46 dfs(n/10,++storey); 47 if(storey==1){ 48 p=n+p+9; 49 // printf("**%d\n",p); 50 return p; 51 } 52 if(storey!=1){ 53 p=p+8*pow(10,--storey); 54 // printf("$$%d\n",p); 55 return p; 56 } 57 } 58 } 59 // 60 //100 61 //101 62 //110 63 //111 64 //1000
POJ1426 1s 10000K(不到10M) 报错TLE
洛谷OJ 3s 0B 报错TLE
可用平台 1s 64M 报错MLE
但奇怪为啥三个平台报错一个内存超一个时间超,而且同样代码,在时间要求更宽泛洛谷上反而时间超时,在内存要求宽泛的可用平台上反而内存超时
把数据类型改成long long int再提交,他妈的惊了
1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #include<math.h> 5 long long dfs(long long n,int storey); 6 int num;//最初输入 7 int nok;//真正的用于存储输入值num的 8 int flag;//初始化标记,记录输入值num有多少位 9 long long n;//初始化后存于此 10 long long p;//dfs搜索后仅包含0和1的结果 11 12 int isfind; 13 int main() 14 { 15 while(scanf("%d",&num)&&num){ 16 isfind=0; 17 nok=num; 18 flag=1; 19 while(num/10){ 20 num=num/10; 21 flag++; 22 } 23 n=pow(10,flag); 24 25 while(isfind==0) 26 { 27 p=0; 28 if(n%10==0) 29 n++; 30 if(n%10==1){ 31 n=dfs(n,0); 32 if(n%nok==0){ 33 printf("%lld\n",n); 34 isfind=1; 35 } 36 } 37 } 38 } 39 } 40 long long dfs(long long n, int storey) 41 { 42 43 if(n%10==0&&storey!=0) 44 ; 45 46 if((n%10==1)){ 47 dfs(n/10,++storey); 48 if(storey==1){ 49 p=n+p+9; 50 // printf("**%d\n",p); 51 return p; 52 } 53 if(storey!=1){ 54 p=p+8*pow(10,--storey); 55 // printf("$$%d\n",p); 56 return p; 57 } 58 } 59 } 60 // 61 //100 62 //101 63 //110 64 //111 65 //1000
POJ数据弱的简直可以,上次找出那人染色代码打印路径明显的反例,这次也是,洛谷和可用平台还是一个TLE一个MLE,但POJ是AC的
可用平台图标跟POJ一样,题号也是1426但在可用平台里的全局题号是428,可是POJ上AC可用平台MLE,爱了爱了,又是自己造严谨的数据而不是拉过来的哪怕题号一样(等POJ崩了这个可用平台也能完美代替),但这题评分居然是很水~~~~(>_<)~~~~
但这里突然回忆之前博客染色那人的代码,调整if顺序的,最后没调整我也用了个反例使得输出有误,但可用平台的题号还和POJ不一样,却都很水的AC了,证明可用平台有些题目自己造数据有些拉POJ的,跟题号没关系。(那个题好像POJ专属)
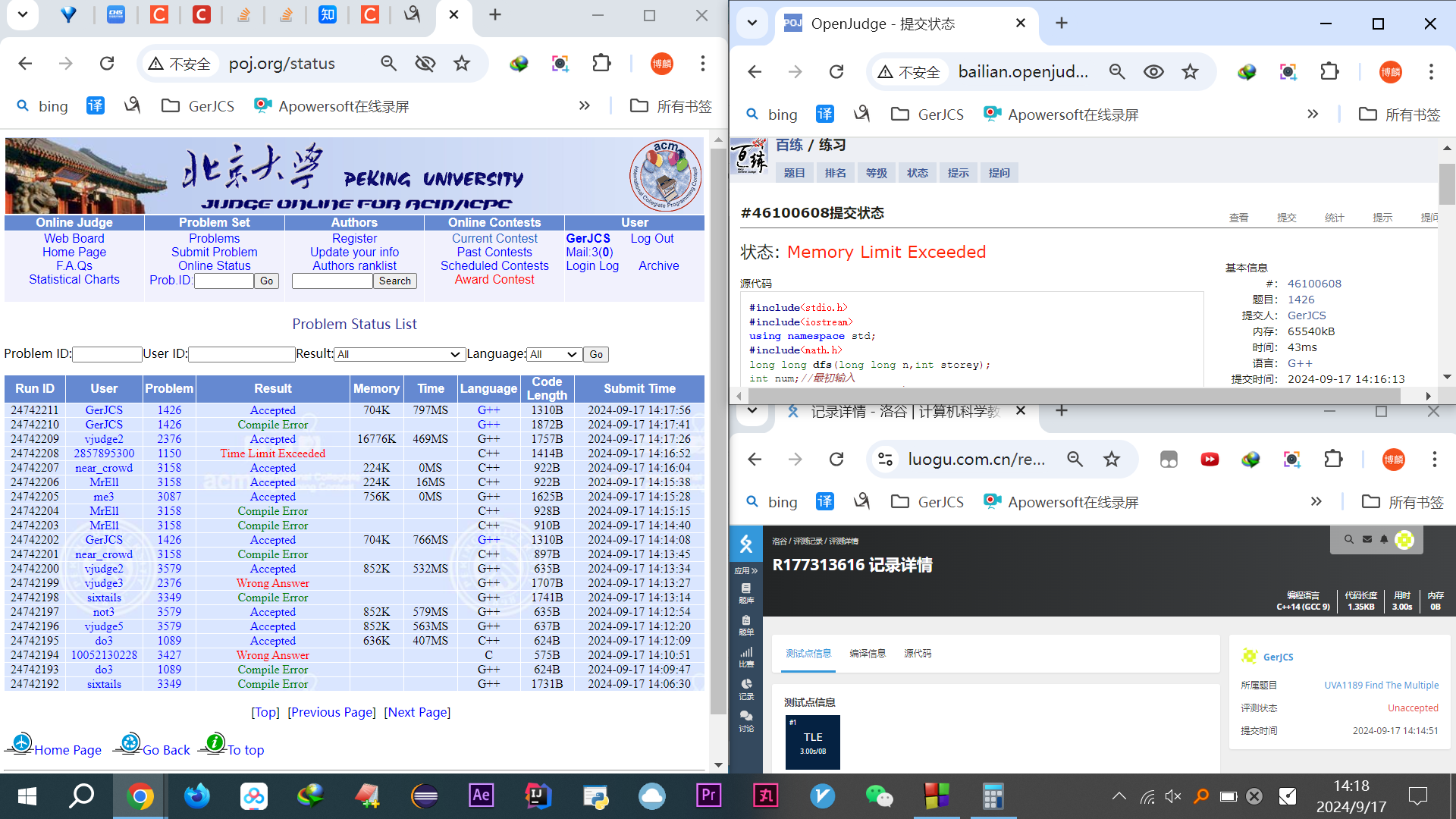
测评机制暂时没必要研究(愧对WYH,一直没空搞他的工蜂oj项目,我还弱先吃上饭再说吧),强行个解释自圆其说得了,猜测,哪怕long long int类型找更久开更大内存,都比int更可能AC,尽管int搜到尽头也没有long long int搜到答案用的时间长,耗的内存多,但偏偏int搜超范围了会TLE/MLE
###:发现for里多个输出真费时间,

1 #include<stdio.h> 2 int main() 3 { 4 for(int i=0;i<1000000;i++) 5 ;// printf("%d",i); 6 }
这段代码加不加printf输出耗时完全不同,上面POJ AC了的代码在29行下加个输出反而直接跑个不停
###:上述代码输入99,输出1111111111111111110,但111111111111111111也是答案,咋会把大的数输出了,检查发现POJ上AC的代码问题太严重了,每次都是没有把n+1的情况,加进入判断并输出
改成严谨的依旧不行

1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #include<math.h> 5 long long dfs(long long n,int storey); 6 int num;//最初输入 7 int nok;//真正的用于存储输入值num的 8 int flag;//初始化标记,记录输入值num有多少位 9 long long n;//初始化后存于此 10 long long p;//dfs搜索后仅包含0和1的结果 11 12 int isfind; 13 int main() 14 { 15 while(scanf("%d",&num)&&num){ 16 isfind=0; 17 nok=num; 18 flag=1; 19 while(num/10){ 20 num=num/10; 21 flag++; 22 } 23 n=pow(10,flag); 24 if(n%nok==0){ 25 printf("%lld\n",n); 26 isfind=1; 27 } 28 while(isfind==0) 29 { 30 p=0; 31 if(n%10==0){ 32 n++; 33 34 35 36 if(n%nok==0){ 37 printf("%lld\n",n); 38 isfind=1; 39 } 40 41 } 42 if(n%10==1){ 43 n=dfs(n,0); 44 if(n%nok==0){ 45 printf("%lld\n",n); 46 isfind=1; 47 } 48 } 49 } 50 } 51 } 52 long long dfs(long long n, int storey) 53 { 54 55 if(n%10==0&&storey!=0) 56 ; 57 58 if((n%10==1)){ 59 dfs(n/10,++storey); 60 if(storey==1){ 61 p=n+p+9; 62 // printf("**%d\n",p); 63 return p; 64 } 65 if(storey!=1){ 66 p=p+8*pow(10,--storey); 67 // printf("$$%d\n",p); 68 return p; 69 } 70 } 71 } 72 // 73 //100 74 //101 75 //110 76 //111 77 //1000
彻底不会了
看题解
封神博客,思路太牛逼了
###:long long int输出用lld llu都行,unsigned long long int在long long int范围之内也可以lld,但超了long long int的范围了必须用llu

1 #include<stdio.h> 2 int main() 3 { 4 long long a=1111111111111111111; 5 unsigned long long b=11111111111111111111; 6 unsigned long long c=1111111111111111111; 7 printf("%lld %llu\n",a,a); 8 printf("%llu\n",b); 9 printf("%lld\n",c); 10 }
long long int和long long是一个东西
真的懒得管类型范围,全网搜到的博客写的一坨屎
重新自己写,尽量避免回忆别人博客里的代码,尽量回忆思路,然后自己写
不会的时候,搜题解诸如“XXX没思路”,然后放大网页,一行一行看,尽量别一下子全看,有点思路就自己写
写了个发现99怎么都不输出
1 #include<stdio.h> 2 #include<math.h> 3 void dfs(long long int nok,int post); 4 int n, pp; 5 int main() 6 { 7 while(scanf("%d",&n)&&n){ 8 int flag=1; 9 int step=n; 10 pp=0; 11 while(step/10){ 12 step=step/10; 13 flag++; 14 } 15 long long int nok; 16 nok=pow(10,flag);//n的初始化值给nok 17 nok=nok/10;//初始化完,下面开板就*10,这里除以10,能把最初始化的值赋给nok,而不至于略过真正初始化的nok 18 dfs(nok, flag+1); 19 } 20 } 21 void dfs( long long int nok,int post) 22 { 23 if(post==19)//是先*10去找,没这个直接干到超范围了 24 return; 25 if(nok%n==0&&pp==0){ 26 printf("%lld\n",nok); 27 pp=1; 28 return; 29 } 30 if(pp==0) 31 { 32 // printf("#%lld\n",nok*10); 33 dfs(nok*10,post+1); 34 // printf("@%lld\n",nok*10); 35 dfs(nok*10+1,post+1); 36 } 37 }
相当诡异,反复冥思苦想终于懂了,原因是我的思路跟他相悖,起手10是根本没办法搜到答案的,比起结论更重要的是掌握找出错误的思路过程,先叙述下找到问题的思路,输入99,无输出,那用32,34行printf,结果等了相当久发现到1000011...11就不输出了,以为是运行内存有个限制,不会一直输出所以停了,又把AC代码printf下所有发现时间太久,没全printf就关掉了,加unsigned发现没啥关系,回去检查初始化发现也没问题,就跟AC代码一样,用dfs(1,1)居然输出了(函数参数不仅可以传递变量也可以传递具体数值),但dfs(10,2)就不行,试了下发现dfs(100,3)也不行,这是为啥啊,我是替你着想想把这个做个优化,因为比如99,倍数只用从100开始就好了,没必要从1,1*10是10,10*10是100这样去走啊。从10或者100开始搜要输出好久,那来个极端的,99应该输出1101111111111111111,总共19位,那我dfs(10000000000000000,17),从17位开始搜,理论上应该乘个2次就会输出结果。结果

一下明白了,他这个1是从最后一位逐渐往前的,如果从100开始,那么深搜到最深处,返回的时候只会返回到100,那么最多就是100后添个1,100100...0,而答案是1111..11,实际要返回到1,然后,多次*10+1变成1111..11。这也是为什么无论输入什么答案都是好多位,因为是深搜到最深处,再返回。
理解后优化下那人的AC代码,没必要传递输入值,也没必要用unsigned

AC代码
1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #include<math.h> 5 void dfs(unsigned long long int nok,int post); 6 int n, pp; 7 int main() 8 { 9 while(scanf("%d",&n)&&n){ 10 pp=0; 11 dfs(1, 1); 12 } 13 } 14 void dfs(unsigned long long nok,int post) 15 { 16 if(post==20)//是先*10去找,没这个直接干到超范围了 17 return; 18 if(nok%n==0&&pp==0){ 19 printf("%lld\n",nok); 20 pp=1; 21 return; 22 } 23 if(pp==0) 24 { 25 // printf("#%llu\n",nok*10); 26 dfs(nok*10,post+1); 27 // printf("@%lld\n",nok*10+1); 28 dfs(nok*10+1,post+1); 29 } 30 }
但可用平台上unsigned没有的话会WA(后面说),long long int最大是9223372036854775807(19位),unsigned最大是18446744073709551615(20位)
实际20位够了,但题目说不超过100位很误导人,让人以为没法用数据类型来运算,但样例输出搞这么多位的数也算是个提示,是深搜递归返回得到的结果
搞了个好玩的,用超时的代码输出所有答案,存到数组里,暴力打表, 0ms0B
打表AC代码

1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #include<math.h> 5 void dfs(unsigned long long int nok,int post); 6 int n, pp; 7 int main() 8 { 9 unsigned long long int map[200]={1 10 ,10 11 ,1000000000000000011 12 ,100 13 ,10 14 ,1000000000000000110 15 ,1000000000000000111 16 ,1000 17 ,1000000000011111111 18 ,10 19 ,100000000000000001 20 ,1000000000000001100 21 ,1000000000000001 22 ,10000000000000010 23 ,1000000000000000110 24 ,10000 25 ,10000000000000101 26 ,1000000000111111110 27 ,1000000000000001101 28 ,100 29 ,10000000000000101 30 ,1000000000000000010 31 ,1000000000000010111 32 ,1000000000000011000 33 ,100 34 ,10000000000000010 35 ,1000000000101111111 36 ,100000000000000100 37 ,1000000000000000111 38 ,1000000000000000110 39 ,1000000000000110011 40 ,100000 41 ,1000000000000101111 42 ,100000000000001010 43 ,10000000000000010 44 ,1000000001111111100 45 ,100000000000000011 46 ,10000000000000110 47 ,10000000000000101 48 ,1000 49 ,1000000000000010111 50 ,100000000000001010 51 ,1000000000000010101 52 ,100000000000000100 53 ,1000000000111111110 54 ,100000000000001110 55 ,1000000000000101 56 ,1000000000000110000 57 ,1000000000000011101 58 ,100 59 ,10000000000000101 60 ,100000000000000100 61 ,1000000000000000011 62 ,1000000001101111110, 63 1000000000000000010, 64 1000000000000001000, 65 1000000000000011, 66 1000000000000001010, 67 10000000000000011, 68 1000000000000001100, 69 1000000000000011, 70 100000000001110010, 71 1000000001011101111, 72 1000000, 73 10000000000000010, 74 1000000000000111110, 75 100000000000011, 76 1000000000000010100, 77 100000000000011, 78 10000000000000010, 79 1000000000000100101, 80 1000000011111111000, 81 1000000000001, 82 1000000000000000110, 83 1000000000000001100, 84 100000000000001100, 85 1000000000000001, 86 100000000000001010, 87 100000000000110001, 88 10000, 89 1000000000111111101, 90 1000000000000110110, 91 100000000000001101, 92 1000000000000010100, 93 100000000000001010, 94 100000000000010010, 95 100000000000000101, 96 1000000000000001000, 97 1000000000000011011, 98 1000000000111111110, 99 1000000000000001, 100 1000000000000011100, 101 1000000000001111001, 102 10000000000001010, 103 10000000000000110, 104 1000000000001100000, 105 100000000001111, 106 1000000000000111110, 107 1101111111111111111, 108 100, 109 1000000000000000001, 110 100000000000001010, 111 100000000000000001, 112 1000000000000001000, 113 100000000000001010, 114 100000000010000110, 115 10000000000001001, 116 1000000001111111100, 117 1000000000001000011, 118 1000000000000000010, 119 100000000000000011, 120 100000000000110000, 121 1000000000000111101, 122 10000000000000110, 123 100000000000001110, 124 10000000000000100, 125 1000000001101111101, 126 100000000000000110, 127 10000000000000101, 128 1000000000000011000, 129 1000000000000101111, 130 10000000000000110, 131 1000000001100011001, 132 1000000000011100100, 133 1000, 134 1000000001111011110, 135 1000000000000110101, 136 10000000, 137 10000000000001001, 138 10000000000000010, 139 10000000001101, 140 1000000000010111100, 141 1000000000001010001, 142 1000000000000110, 143 1000000001101111110, 144 100000000000111000, 145 1000000000001, 146 1000000000000110, 147 1000000000001001111, 148 100000000000000100, 149 1000000000000101, 150 1000000000011110, 151 1000000000000001, 152 1000000111111110000, 153 1000000000000001010, 154 10000000000010, 155 100000000000011111, 156 1000000000000010100, 157 10000000000001111, 158 1000000000000001100, 159 1000000000010111001, 160 1000000000000011000, 161 1000000000111111101, 162 10000000000000010, 163 100000000001110010, 164 1000000000000010100, 165 1000000000000101, 166 1000000000001100010, 167 1000000000000000011, 168 100000, 169 1000000000001101001, 170 100000000111111110, 171 1000000000011011101, 172 1000000000001110100, 173 1000000000000111110, 174 1000000000000011010, 175 1000000000001001101, 176 10000000000011000, 177 1000000000001100111, 178 100000000000001010, 179 1000000000111111011, 180 1000000000000100100, 181 1000000000000010111, 182 1000000000000001010, 183 100000000000000100, 184 100000000000010000, 185 10000000000000011, 186 100000000000001110, 187 1000000000000100111, 188 1000000001111111100, 189 10000000000000111, 190 10000000000000010, 191 1000000000000011, 192 100000000000011000, 193 1000000000000000110, 194 10000000001101110, 195 100000000001001001, 196 100000000000010100, 197 1000000010111010111, 198 10000000000000110, 199 1000000000011111101, 200 1000000000011000000, 201 1000000010000100001, 202 1000000000011110, 203 100000000000001010, 204 100000000010010100, 205 100000000000111001, 206 1111111111111111110, 207 1000000000101111001, 208 1000}; 209 while(scanf("%d",&n)&&n){ 210 printf("%llu\n",map[n-1]); 211 } 212 }
这里POJ的10000K,是10000KB还是Kb啥,B/b可以省略的吗?
洛谷OJ的0B,不应该是0K吗?查了几个解释、参考博客、参考博客看的我头大,一方面要辨别博客的正确性(发现好多写的不对的),一方面oj本身写的可能也有问题,先搁置
测试198是最大的19位,1111111111111111110

1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #include<math.h> 5 void dfs(unsigned long long int nok,int post); 6 int n, pp; 7 unsigned long long int map[200]={1 8 ,10 9 ,1000000000000000011 10 ,100 11 ,10 12 ,1000000000000000110 13 ,1000000000000000111 14 ,1000 15 ,1000000000011111111 16 ,10 17 ,100000000000000001 18 ,1000000000000001100 19 ,1000000000000001 20 ,10000000000000010 21 ,1000000000000000110 22 ,10000 23 ,10000000000000101 24 ,1000000000111111110 25 ,1000000000000001101 26 ,100 27 ,10000000000000101 28 ,1000000000000000010 29 ,1000000000000010111 30 ,1000000000000011000 31 ,100 32 ,10000000000000010 33 ,1000000000101111111 34 ,100000000000000100 35 ,1000000000000000111 36 ,1000000000000000110 37 ,1000000000000110011 38 ,100000 39 ,1000000000000101111 40 ,100000000000001010 41 ,10000000000000010 42 ,1000000001111111100 43 ,100000000000000011 44 ,10000000000000110 45 ,10000000000000101 46 ,1000 47 ,1000000000000010111 48 ,100000000000001010 49 ,1000000000000010101 50 ,100000000000000100 51 ,1000000000111111110 52 ,100000000000001110 53 ,1000000000000101 54 ,1000000000000110000 55 ,1000000000000011101 56 ,100 57 ,10000000000000101 58 ,100000000000000100 59 ,1000000000000000011 60 ,1000000001101111110, 61 1000000000000000010, 62 1000000000000001000, 63 1000000000000011, 64 1000000000000001010, 65 10000000000000011, 66 1000000000000001100, 67 1000000000000011, 68 100000000001110010, 69 1000000001011101111, 70 1000000, 71 10000000000000010, 72 1000000000000111110, 73 100000000000011, 74 1000000000000010100, 75 100000000000011, 76 10000000000000010, 77 1000000000000100101, 78 1000000011111111000, 79 1000000000001, 80 1000000000000000110, 81 1000000000000001100, 82 100000000000001100, 83 1000000000000001, 84 100000000000001010, 85 100000000000110001, 86 10000, 87 1000000000111111101, 88 1000000000000110110, 89 100000000000001101, 90 1000000000000010100, 91 100000000000001010, 92 100000000000010010, 93 100000000000000101, 94 1000000000000001000, 95 1000000000000011011, 96 1000000000111111110, 97 1000000000000001, 98 1000000000000011100, 99 1000000000001111001, 100 10000000000001010, 101 10000000000000110, 102 1000000000001100000, 103 100000000001111, 104 1000000000000111110, 105 1101111111111111111, 106 100, 107 1000000000000000001, 108 100000000000001010, 109 100000000000000001, 110 1000000000000001000, 111 100000000000001010, 112 100000000010000110, 113 10000000000001001, 114 1000000001111111100, 115 1000000000001000011, 116 1000000000000000010, 117 100000000000000011, 118 100000000000110000, 119 1000000000000111101, 120 10000000000000110, 121 100000000000001110, 122 10000000000000100, 123 1000000001101111101, 124 100000000000000110, 125 10000000000000101, 126 1000000000000011000, 127 1000000000000101111, 128 10000000000000110, 129 1000000001100011001, 130 1000000000011100100, 131 1000, 132 1000000001111011110, 133 1000000000000110101, 134 10000000, 135 10000000000001001, 136 10000000000000010, 137 10000000001101, 138 1000000000010111100, 139 1000000000001010001, 140 1000000000000110, 141 1000000001101111110, 142 100000000000111000, 143 1000000000001, 144 1000000000000110, 145 1000000000001001111, 146 100000000000000100, 147 1000000000000101, 148 1000000000011110, 149 1000000000000001, 150 1000000111111110000, 151 1000000000000001010, 152 10000000000010, 153 100000000000011111, 154 1000000000000010100, 155 10000000000001111, 156 1000000000000001100, 157 1000000000010111001, 158 1000000000000011000, 159 1000000000111111101, 160 10000000000000010, 161 100000000001110010, 162 1000000000000010100, 163 1000000000000101, 164 1000000000001100010, 165 1000000000000000011, 166 100000, 167 1000000000001101001, 168 100000000111111110, 169 1000000000011011101, 170 1000000000001110100, 171 1000000000000111110, 172 1000000000000011010, 173 1000000000001001101, 174 10000000000011000, 175 1000000000001100111, 176 100000000000001010, 177 1000000000111111011, 178 1000000000000100100, 179 1000000000000010111, 180 1000000000000001010, 181 100000000000000100, 182 100000000000010000, 183 10000000000000011, 184 100000000000001110, 185 1000000000000100111, 186 1000000001111111100, 187 10000000000000111, 188 10000000000000010, 189 1000000000000011, 190 100000000000011000, 191 1000000000000000110, 192 10000000001101110, 193 100000000001001001, 194 100000000000010100, 195 1000000010111010111, 196 10000000000000110, 197 1000000000011111101, 198 1000000000011000000, 199 1000000010000100001, 200 1000000000011110, 201 100000000000001010, 202 100000000010010100, 203 100000000000111001, 204 1111111111111111110, 205 1000000000101111001, 206 1000}; 207 int j; 208 int main() 209 { 210 unsigned long long int max=1; 211 for(int i=0;i<200;i++){ 212 if(max<map[i]){ 213 max=map[i]; 214 j=i; 215 } 216 } 217 cout<<max<<" "<<j; 218 // while(scanf("%d",&n)&&n){ 219 // printf("%llu\n",map[n-1]); 220 // } 221 }
为啥210行的绿色max放到main外面,全局变量就噼里啪啦报错,说是不明确没指定,但放在main里面就没任何问题。
绿色int queue也是,放哪都不行
同样绿色map为啥咋放都没事,记得之前有过这个问题搁置了
###:
没必要用unsigned
###:无意间发现的不错的总结
###:回过头看上面代码,其实不是unsigned会WA,是 if(post==19) return; 这句话应该放下面,if顺序影响答案,跟之前那人染色思路的不同,那个怎么走,都是同样权位优先级的,颠倒顺序错了就是代码有问题,过了就是平台数据太弱,而这个需要先是判断输出再做返回。
综上
long long int类型19位的AC代码
1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #include<math.h> 5 void dfs( long long int nok,int post); 6 int n, pp; 7 int main() 8 { 9 while(scanf("%d",&n)&&n){ 10 pp=0; 11 dfs(1, 1); 12 } 13 } 14 void dfs(long long nok,int post) 15 { 16 if(nok%n==0&&pp==0){ 17 printf("%lld\n",nok); 18 pp=1; 19 return; 20 } 21 if(post==19) 22 return; 23 if(pp==0) 24 { 25 dfs(nok*10,post+1); 26 dfs(nok*10+1,post+1); 27 } 28 }
一开始把21,22行放到了上一个判断前面,故WA了
这些人这是有趣,代码就跟不是自己写的似得,上一道题那人的染色思路代码中,“力荐!!” 的注释给了我找他反例的启发
这人的“必须是unsigned”,都写了自己就不试一下吗,而且也没像我似得21,22颠倒
###再看另一个人的博客,思路一样只是改成了广搜,开心的是这家伙好像也在刷邝斌飞专题
这道题没必要再写一遍了,重点是搜索的逻辑
###: 记得WYH说先看对不对,再看超不超时 1s是10^9 ,但这题没法这么搞没法确定哪个数输出是大的,没法分开打表输出
###:越来越喜欢这个可用平台了,且每次做完题都会看看洛谷的讨论(那个叫唐一文的笑死我了,也太可爱了)
这些人思路真广真花花,不咋想看了

q神不看别人代码慰藉
强迫看懂别人代码
但好拉扯
回忆快速gcd
中国剩余定理
快排
西工大姜学峰教练没有搞不到的题
数一不透露西安区域赛题目
辗转相除法
但看到有个东西叫高精度(之前听过),试验了下牛死了,必须学下

1 #include<iostream> 2 #include<string> 3 using namespace std; 4 int a[301],b[301],c[302]; 5 int init(int a[]) 6 { 7 string s; 8 cin>>s; 9 int len=s.size(); 10 printf("len %d\n",len); 11 for(int i=0;i<len;i++){ 12 a[i]=s[len-1-i]-'0'; 13 printf("%d\n",a[i]); 14 } 15 // for(int i=0;i<len;i++) 16 // printf("%d",a[i]); 17 return len; 18 } 19 int main() 20 { 21 int lena=init(a); 22 int lenb=init(b); 23 printf("######%d %d\n",lena,lenb); 24 25 int lenc=max(lena,lenb); 26 for(int i=0;i<lenc;i++) 27 { 28 c[i]+=a[i]+b[i]; 29 if(c[i]>=10) 30 { 31 c[i+1]++; 32 c[i]%=10; 33 } 34 } 35 36 while(c[lenc]==0 && lenc>0) 37 lenc--; 38 for(int i=lenc;i>=0;i--) 39 cout<<c[i]; 40 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号