POJ3278 Catch That Cow
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 222142 | Accepted: 67092 |
Description
Farmer John has been informed of the location of a fugitive cow and wants to catch her immediately. He starts at a point N (0 ≤ N ≤ 100,000) on a number line and the cow is at a point K (0 ≤ K ≤ 100,000) on the same number line. Farmer John has two modes of transportation: walking and teleporting.
* Walking: FJ can move from any point X to the points X - 1 or X + 1 in a single minute
* Teleporting: FJ can move from any point X to the point 2 × X in a single minute.
If the cow, unaware of its pursuit, does not move at all, how long does it take for Farmer John to retrieve it?
Input
Output
Sample Input
5 17
Sample Output
4
Hint
*步行:FJ可以在一分钟内从任何一个点X移动到点X-1或X+1
*传送:FJ可以在一分钟内从任何一个X点移动到2*X点
输出FJ抓带到奶牛需要的最短时间,以分钟为单位
思路:
明显的BFS,几年没摸,彻底重新回顾BFS(已经毫无印象,连void还是int,参数是什么都自己想,想需要什么,而不是回忆),手写结构体构造先进先出的队列
AC代码:POJ 手写数组模拟队列写法不涉及C++的STLqueue 该代码HdojWA

1 #include<stdio.h> 2 int iswalk[100050]; 3 int p;//实时移动数组下标,视作队尾添加 4 int q;//取数,视作队头出队 5 int N, K; 6 struct trajectory 7 { 8 int step; 9 int num; 10 }; 11 struct trajectory tra[100050]; 12 int main() 13 { 14 scanf("%d %d", &N, &K); 15 tra[q].num = N; 16 tra[q].step = 0; 17 iswalk[N] = 1; 18 while(q <= p) 19 { 20 if(tra[q].num == K){ 21 printf("%d\n", tra[q].step); 22 break; 23 } 24 else 25 { 26 if(iswalk[tra[q].num - 1] == 0 && (tra[q].num - 1 >= 0) && (tra[q].num - 1) <= 100000){ 27 iswalk[tra[q].num - 1] = 1; 28 p ++; 29 tra[p].num = tra[q].num - 1; 30 tra[p].step = tra[q].step + 1; 31 } 32 if(iswalk[tra[q].num + 1] == 0 && (tra[q].num + 1 >= 0) && (tra[q].num + 1) <= 100000){ 33 iswalk[tra[q].num + 1] = 1; 34 p ++; 35 tra[p].num = tra[q].num + 1; 36 tra[p].step = tra[q].step + 1; 37 } 38 if(iswalk[tra[q].num * 2] == 0 && (tra[q].num * 2) >= 0 && (tra[q].num * 2) <= 100000){ 39 iswalk[tra[q].num * 2] = 1; 40 p ++; 41 tra[p].num = tra[q].num * 2; 42 tra[p].step = tra[q].step + 1; 43 } 44 q ++; 45 } 46 } 47 }
注:11行的 struct trajectory tra[100050]; 查过许多文章都说要加,甚至需要typedef,实践发现没必要加struct,直接 trajectory tra[100050]; 即可
注:这是poj,hdoj需要输入多组数据,必须初始化清空上一次的数据,所以该poj上AC的代码,hdoj是WA的,加上16,17,18行的初始化就AC了
AC代码:HDOJ 手写数组模拟队列写法不涉及C++的STLqueue

1 #include<stdio.h> 2 #include<string.h> 3 int iswalk[100050]; 4 int p;//实时移动数组下标,视作队尾添加 5 int q;//取数,视作队头出队 6 int N, K; 7 struct trajectory 8 { 9 int step; 10 int num; 11 }; 12 struct trajectory tra[100050]; 13 int main() 14 { 15 while(scanf("%d %d", &N, &K)!=EOF){ 16 p=0; 17 q=0; 18 memset(iswalk, 0, sizeof(iswalk)); 19 tra[q].num = N; 20 tra[q].step = 0; 21 iswalk[N] = 1; 22 while(q <= p) 23 { 24 if(tra[q].num == K){ 25 printf("%d\n", tra[q].step); 26 break; 27 } 28 else 29 { 30 if(iswalk[tra[q].num - 1] == 0 && (tra[q].num - 1 >= 0) && (tra[q].num - 1) <= 100000){ 31 iswalk[tra[q].num - 1] = 1; 32 p ++; 33 tra[p].num = tra[q].num - 1; 34 tra[p].step = tra[q].step + 1; 35 } 36 if(iswalk[tra[q].num + 1] == 0 && (tra[q].num + 1 >= 0) && (tra[q].num + 1) <= 100000){ 37 iswalk[tra[q].num + 1] = 1; 38 p ++; 39 tra[p].num = tra[q].num + 1; 40 tra[p].step = tra[q].step + 1; 41 } 42 if(iswalk[tra[q].num * 2] == 0 && (tra[q].num * 2) >= 0 && (tra[q].num * 2) <= 100000){ 43 iswalk[tra[q].num * 2] = 1; 44 p ++; 45 tra[p].num = tra[q].num * 2; 46 tra[p].step = tra[q].step + 1; 47 } 48 q ++; 49 } 50 } 51 } 52 }
=================================—分割线—=================================
起手错误写法:
铺垫:看题目POJ3984时回忆了下基本语法:scanf(scanf输入类型为%c,输入其他类型的时候先不研究)、回车、占位符
练习

1 #include<stdio.h> 2 int main() 3 { 4 char a, b, c; 5 int maze[5][5]; 6 //scanf("%d%d%d", &a, &b, &c); 7 scanf("%c-%c-%c", &a, &b, &c);//输入rgb 8 //printf("%c%c%c\n", a, b, c); 9 printf("%c\n%c\n%c", a, b, c); 10 }
一:for的DFS(对应题目为POJ3984,同为BFS,写不明白BFS于是推翻并找到POJ3278奶牛这个基础题来写,但可以看出思路上的问题)

1 #include<stdio.h> 2 int dir[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; 3 int bfs(int x, int y); 4 int maze[5][5]; 5 int step; 6 int evestep[25][2];//记录轨迹 7 int OnGo[5][5];//是否走过这个点 8 int main() 9 //int dir[4][2] = {(-1, 0), (1, 0), (0, -1), (0, 1)}; 10 { 11 // int step; 12 for(int i = 0; i < 5; i ++) 13 for(int j = 0; j < 5; j ++) 14 scanf("%d", &maze[i][j]); 15 int x = 0, y = 0; 16 OnGo[0][0] == 1; 17 // int bfs(x, y); 18 bfs(x, y); 19 } 20 int bfs(int x, int y) 21 { 22 for(int i = 0; i < 4; i ++) 23 { 24 x += dir[i][0]; 25 y += dir[i][1]; 26 if(maze[x][y] == 1 || x < 0 || y < 0 || x > 4 || y > 4) 27 continue; 28 else if(maze[x][y] == 0 && OnGo[x][y] == 0) 29 { 30 OnGo[x][y] == 1; 31 step++; 32 evestep[step][0] = x; 33 evestep[step][1] = y; 34 bfs(x, y); 35 } 36 } 37 //} 38 //推翻重写,昨天写的是DFS 39 40 //BFS
二:推翻重写后,依旧是DFS的思路(因为会顺序进入每一个if),以为BFS会携带每一层的step,return和else大括号效果一样的

1 #include<stdio.h> 2 int tra[100050]; 3 int iswalk[100050]; 4 int p, q, N, K;int flag;int stepans; 5 int bfs(int FJ_x, int step) 6 { 7 if(FJ_x == K){ 8 printf("FJ_x:%d K:%d step:%d\n", FJ_x, K, step); 9 return step;//可有可无 10 } 11 else 12 { 13 if((FJ_x - 1) >= 0 && iswalk[FJ_x - 1] == 0){ 14 iswalk[FJ_x - 1] = 1; 15 step ++; 16 printf("!%d %d\n", FJ_x - 1, step); 17 bfs(FJ_x - 1, step); 18 printf("^%d %d\n", FJ_x -1, step); 19 step --; 20 } 21 if((FJ_x + 1) >= 0 && iswalk[FJ_x + 1] == 0){ 22 iswalk[FJ_x + 1] = 1; 23 step ++; 24 printf("#%d %d\n", FJ_x + 1, step); 25 bfs(FJ_x + 1, step); 26 printf("##%d %d\n", FJ_x+1, step); 27 step --; 28 } 29 if((FJ_x * 2) >= 0 && iswalk[FJ_x * 2] == 0){ 30 iswalk[FJ_x * 2] = 1; 31 step ++; 32 printf("@%d %d\n", FJ_x * 2, step); 33 bfs(FJ_x * 2, step); 34 printf("@@%d %d\n", FJ_x*2, step); 35 step --; 36 } 37 } 38 } 39 int main() 40 { 41 scanf("%d %d", &N, &K); 42 iswalk[N] = 1; 43 printf("%d\n", bfs(N, 0)); 44 }
代码里去掉else只剩下括号里面的几个if效果是一样的
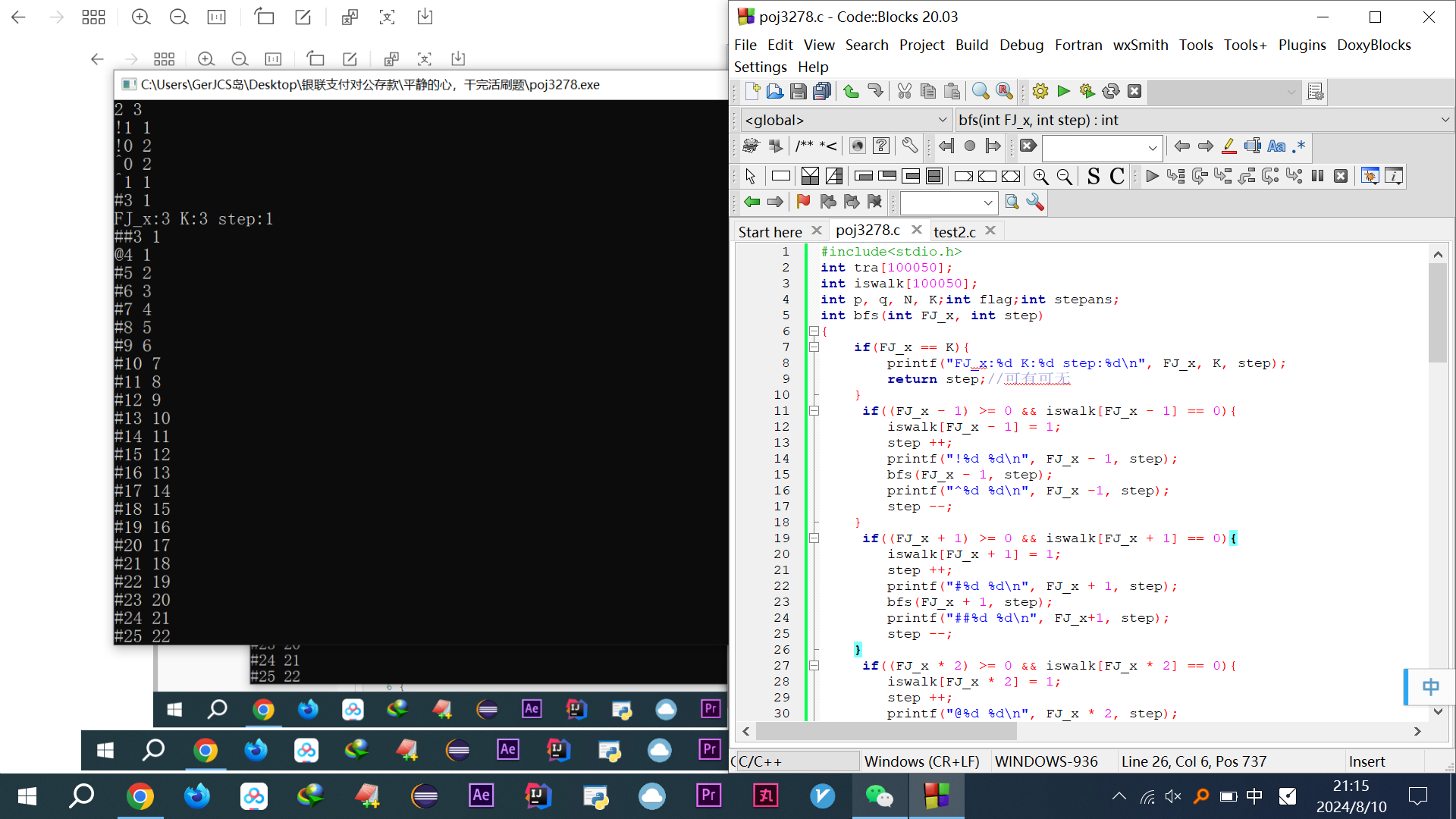
这种写法的printf更便于观察问题
但执行死循环了,截了个图来对着代码脑海里一条一条执行,如下图得知,写法的错误之处是没剪枝,2→1→0递出去,归回来0→1,1其实是2-1,那继续下一个if,2+1,进入3,3返回,2*2=4,进入4,4-1走过但没回溯,就一发不可收拾,一直死循环5、6、7、8..................,其实回溯再加min判断就对了,不懂为啥要回溯就用2 4这个数据,代入上面代码就知道了
三:捡回来BFS后,写出AC代码(发现必须要用到结构体,这是不用C++队列库函数的情况下,最基本的写法,不能再去掉东西了,结构体去了就没法写BFS了),但期间又遇到几个问题,展开复习经典递归:斐波那契数列(点开下面的相关视频“自然和数学之间的神奇联系,兔子的秘密:斐波那契数”),递归是特殊的嵌套函数,展示段代码

1 #include<stdio.h> 2 int tra[100050]; 3 int iswalk[100050]; 4 int p, q, N, K; 5 int flag; 6 int stepans; 7 int bfs(int FJ_x, int step) 8 { 9 if(FJ_x == K){ 10 printf("FJ_x:%d K:%d step:%d\n", FJ_x, K, step); 11 flag = 1; 12 stepans = step; 13 return step;//可有可无 14 } 15 if(flag == 0 && (FJ_x - 1) >= 0 && iswalk[FJ_x - 1] == 0){ 16 iswalk[FJ_x - 1] = 1; 17 step ++; 18 printf("!%d %d\n", FJ_x - 1, step); 19 bfs(FJ_x - 1, step); 20 step --; 21 printf("^%d %d\n", FJ_x, step); 22 } 23 if(flag == 0 && (FJ_x + 1) >= 0 && iswalk[FJ_x + 1] == 0){ 24 iswalk[FJ_x + 1] = 1; 25 step ++; 26 printf("#%d %d\n", FJ_x + 1, step); 27 bfs(FJ_x + 1, step); 28 step --; 29 printf("##%d %d\n", FJ_x, step); 30 } 31 if(flag == 0 && (FJ_x * 2) >= 0 && iswalk[FJ_x * 2] == 0){ 32 iswalk[FJ_x * 2] = 1; 33 step ++; 34 printf("@%d %d\n", FJ_x * 2, step); 35 bfs(FJ_x * 2, step); 36 step --; 37 printf("@@%d %d\n", FJ_x, step); 38 } 39 } 40 int main() 41 { 42 iswalk[0] = 0; 43 scanf("%d %d", &N, &K); //0 1 2 3 N4 5 K6 //5 6 44 iswalk[N] = 1; 45 iswalk[K] = 0; 46 // bfs(N, 0); 47 // printf("%d\n", stepans); 48 printf("%d\n", bfs(N, 0)); 49 }
由于没记录min,输入任何值都输出1,不知为何。只有将48行改用46、47行才行,必须输出stepans才行(或者在38和39行之间加一个return stepans,解题逻辑是错误的但针对int函数的返回值问题是没问题的,不至于没警告和报错却输出的奇奇怪怪的1),而且return根本不跳出函数,而且只是跳出那一层循环。
输入5,6,那到达6之后,还会继续下面的执行,我加了个flag才行 。
而如果把bfs里所有语句都注释掉,则输出的是N的值,奇妙的函数,先搁置(虽然代码明显有逻辑问题,是个深搜的错误版,只走了单支,没比较更新最短step,也没回溯)
这种会把所有情况都跑完,return只会剪枝,不会作为函数终止条件而直接去main主函数里输出结果(其实本身得到的也是错误的数值),如下图(其实没回溯,加个回溯和比较变量更新最小值就对了应该):
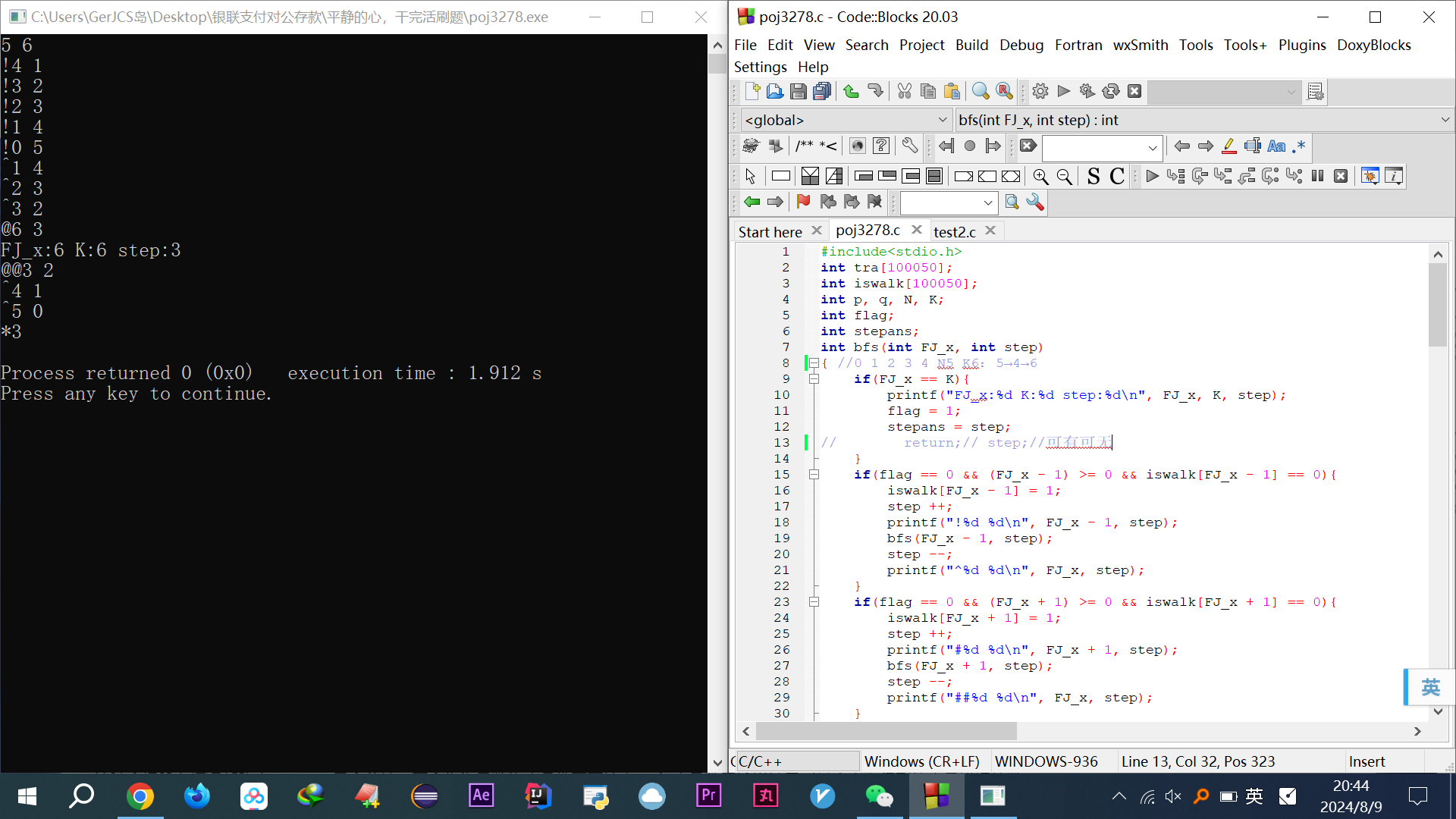
输入5,6,按照5→4→3→6,共3步,视为最小输出的显然不对。
又去回顾递归真正含义,并不会某一个地方退出,只会递出去再归回来,接着又去查了下BFS和DFS的终止条件,粘出里面代码(必须为cpp后缀),输入5,9,执行走一遍,自己唯独加了22和25两行,发现其实就是一条路走下去,返回来再走分叉,其实这个执行过程又有点队列的意思,6进,以6为变量代入一个新的solve,又6+1=7,以7为变量代入一个新的solve,7+1=8,以8为变量代入一个新的solve,遇到9了,发现5→678→9这个路线要4步,规定好最少步骤即最小值为无穷大,对比后将4最为最小值,大于等于4就别走了return,vis要加100是因为范围可能为负数,
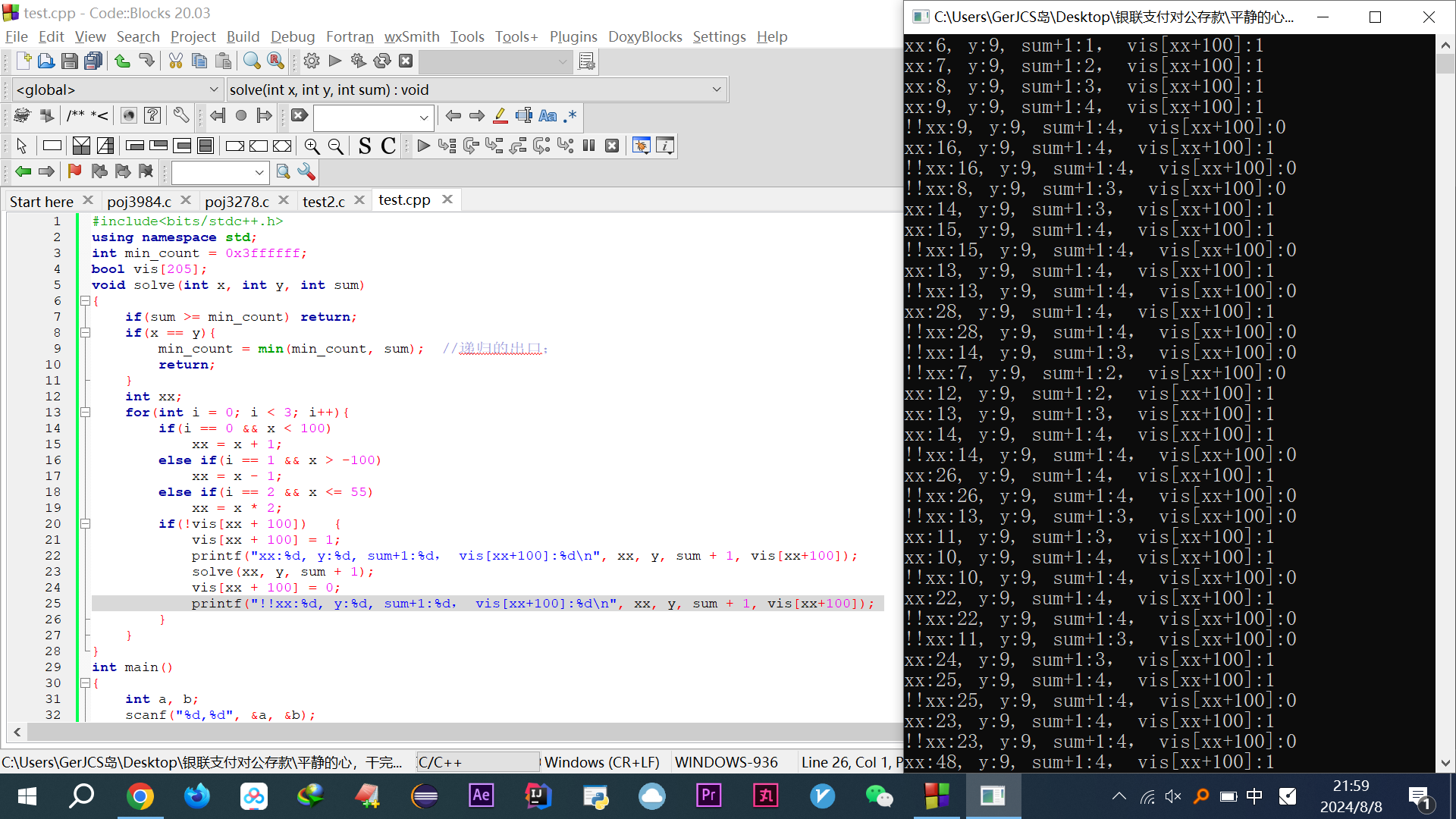
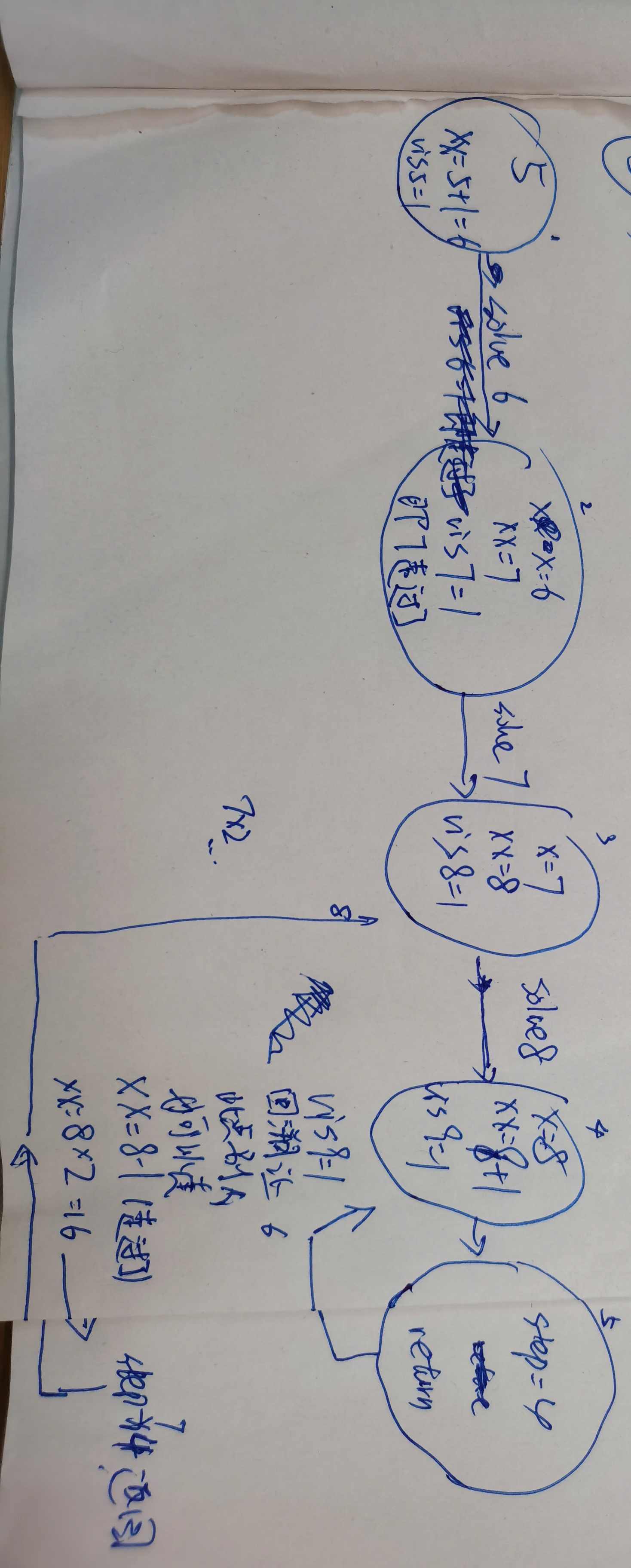
如果vis不重新赋值为0,那么56789这条路线9已经被占用了,step就是4,接下来判断是否走过的条件存在,9永远无法再进入solve,即永远为4,但其实5,9输出为2,而为什么要加判断是否走过的条件,为了减少不必要的solve函数执行甚至死循环,比如上图中“xx=8-1(走过了)”这句话,如果之前没有vis7=1,7就会再一次进入函数,而567898这到9目前算出最少步骤为4,到8最少步骤为3,那再折回去变5就毫无意义,诸如此类会导致程序死循环一直跑下去。
其实不管题目的正解是BFS还是DFS,用两种思路都想一遍,会找到很多共通之处,也会更加理解两种算法
另外终止条件文章里,用的是void,调用solve后返回的是最小值min_count。如果sovle是int类型的,26行的return没有会警告,且输出的值也是随机的,C语言就没有这些警告,随意输出值错误半天找不到原因。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int min_count = 0x3ffffff; 4 bool vis[205]; 5 int solve(int x, int y, int sum) 6 { 7 if(sum >= min_count) return min_count; 8 if(x == y){ 9 min_count = min(min_count, sum); //递归的出口; 10 return min_count; 11 } 12 int xx; 13 for(int i = 0; i < 3; i++){ 14 if(i == 0 && x < 100) 15 xx = x + 1; 16 else if(i == 1 && x > -100) 17 xx = x - 1; 18 else if(i == 2 && x <= 55) 19 xx = x * 2; 20 if(!vis[xx + 100]){ 21 vis[xx + 100] = 1; 22 solve(xx, y, sum + 1); 23 vis[xx + 100] = 0; //回溯很重要,这是在要到达同一个目标时,要记得回溯; 24 } 25 } 26 return min_count; 27 } 28 int main() 29 { 30 int a, b; 31 scanf("%d,%d", &a, &b); 32 int sum = 0; 33 vis[a + 100] = 1; 34 printf("%d\n", solve(a, b, sum)); 35 return 0; 36 }
不错的训练深搜DFS的思路,但代码提交以后TLE是正常的因为深搜时间复杂度超了,但居然提示CE。
查了下换成GCC和G++才TLE,据说POJ编译器有问题??这么广泛使用的OJ不会存在这种问题吧?
这是我的代码:http://poj.org/showsource?solution_id=24729057
对应的CE报错:http://poj.org/showcompileinfo?solution_id=24729057,真无语各种说变量未定义少分号啥的
同类问题、同类问题、而且还不能用万能头函数、poj提交C语言代码莫名其妙ce
DFS和BFS时间复杂度(待回顾)
四:写的时候发现另一个问题,贼拉奇怪,if还是else if又搞不明白了。
16行printf输出语句,注释掉与否,输入1 2,运行出两种不同的结果,注释掉整个最后俩else if,结果又不同
1 #include<stdio.h> 2 int tra[100050]; 3 int iswalk[100050]; 4 int p, q, N, K;int flag;int stepans; 5 int bfs(int FJ_x, int step) 6 { 7 if(FJ_x == K){ 8 printf("FJ_x:%d K:%d step:%d\n", FJ_x, K, step); 9 return step;//可有可无 10 } 11 else if((FJ_x - 1) >= 0 && iswalk[FJ_x - 1] == 0){ 12 iswalk[FJ_x - 1] = 1; 13 step ++; 14 printf("!%d %d\n", FJ_x - 1, step); 15 bfs(FJ_x - 1, step); 16 printf("^%d %d\n", FJ_x -1, step); 17 step --; 18 } 19 else if((FJ_x + 1) >= 0 && iswalk[FJ_x + 1] == 0){ 20 iswalk[FJ_x + 1] = 1; 21 step ++; 22 printf("#%d %d\n", FJ_x + 1, step); 23 bfs(FJ_x + 1, step); 24 printf("##%d %d\n", FJ_x+1, step); 25 step --; 26 } 27 else if((FJ_x * 2) >= 0 && iswalk[FJ_x * 2] == 0){ 28 iswalk[FJ_x * 2] = 1; 29 step ++; 30 printf("@%d %d\n", FJ_x * 2, step); 31 bfs(FJ_x * 2, step); 32 printf("@@%d %d\n", FJ_x*2, step); 33 step --; 34 } 35 } 36 int main() 37 { 38 scanf("%d %d", &N, &K); 39 iswalk[N] = 1; 40 printf("%d\n", bfs(N, 0)); 41 }

图虽然很模糊但大概可以看出,
注释掉俩else if外加16行的printf的时候,输入1 2,输出2,而且没有8行那个输出效果,则没进入第一个if,把这7-10都注释掉又输出0了(大惑不解)
仅注释掉16行的printf的时候,输入1 2,输出1
仅注释掉俩else if的时候,输入1 2,输出5
啥都不注释的时候,输入1 2,输出5
注释掉只剩第一个else if的时候,输入1 2,输出5(大惑不解)
根据超级链接1,写了段代码实在不知道啥原因

1 #include<stdio.h> 2 int tra[100050]; 3 int iswalk[100050]; 4 int p, q, N, K;int flag;int stepans; 5 int bfs(int FJ_x, int step) 6 { 7 if((FJ_x - 1) >= 0 && iswalk[FJ_x - 1] == 0){ 8 iswalk[FJ_x - 1] = 1; 9 step ++; 10 printf("!%d %d\n", FJ_x - 1, step); 11 bfs(FJ_x - 1, step); 12 printf("^%d %d\n", FJ_x -1, step); 13 step --; 14 } 15 } 16 int main() 17 { 18 scanf("%d %d", &N, &K); 19 iswalk[N] = 1; 20 printf("%d\n", bfs(N, 0)); 21 } 22 //输入1 2输出5 23 //注释掉12行的printf,输入1 2,输出0
于是查int函数没return对结果的影响,超级链接1、超级链接2、超级链接3(有空学一学反编译汇编啥的吧)
测试了下:
1 #include<stdio.h> 2 int x; 3 int fn(int y) 4 { 5 printf("#%d\n", y + 1); 6 } 7 int main() 8 { 9 scanf("%d", &x); 10 printf("%d\n", fn(x)); 11 } 12 13 //fn()函数加不加print,最终结果是不同的,先搁置
五:学到另一种思路:(好几个博主都说是深搜,但我觉得有点像二叉树+DP+递归/递推的意思,深搜这个题是TLE的上面说过了,但画出二叉树形状的推导过程又有点像深搜,好奇怪)
C语言写法AC代码

1 #include<stdio.h> 2 int n, k; 3 int step; 4 int min; 5 int dfs(int x) 6 { 7 if(x <= n) 8 { 9 // 只能步行 10 return n - x; 11 } 12 if(x % 2) 13 { 14 // x为奇数 15 int a = dfs(x - 1); 16 int b = dfs(x + 1); 17 if(a<=b) 18 return a+1; 19 else 20 return b+1; 21 } 22 else 23 { 24 // x为偶数 25 int a = x - n; 26 int b = dfs(x / 2) + 1; 27 if(a<=b) 28 return a; 29 else 30 return b; 31 } 32 } 33 34 int main() 35 { 36 scanf("%d %d", &n, &k); 37 if(!n) 38 { 39 step++; 40 n++; 41 } 42 step += dfs(k); 43 printf("%d\n", step); 44 return 0; 45 }
疑惑,感觉这个bfs时间复杂度是n,但修改几个地方提交很奇怪
TLE:

1 #include<stdio.h> 2 int n, k; 3 int step; 4 int dfs(int x) 5 { 6 if(x <= n) 7 { 8 // 只能步行 9 return n - x; 10 } 11 if(x % 2) 12 { 13 // x为奇数 14 if(dfs(x - 1) <= dfs(x + 1)) 15 return dfs(x - 1) + 1; 16 if(dfs(x - 1) > dfs(x + 1)) 17 return dfs(x + 1) + 1; 18 } 19 else 20 { 21 // x为偶数 22 if(x - n <= dfs(x / 2) + 1) 23 return x - n; 24 if(x - n > dfs(x / 2) + 1) 25 return dfs(x / 2) + 1; 26 } 27 } 28 29 int main() 30 { 31 scanf("%d %d", &n, &k); 32 if(!n) 33 { 34 step++; 35 n++; 36 } 37 step += dfs(k); 38 printf("%d\n", step); 39 return 0; 40 }
http://poj.org/showsource?solution_id=24728096
http://poj.org/showsource?solution_id=24728093
http://poj.org/showsource?solution_id=24728094

思路上一开始只画了代码写的判断部分,想不通为何偶数不用把左一步右一步也加进来比较,把所有可能都画出来就理解了,如图叉掉的是显然应该剪枝的。

或者这样理解,奇数要从左一步或者右一步到这里,偶数除了一步一步往回走比如22 24这种,还有就是2倍关系,偶数不涉及奇数那种左走一步或者右走一步过来的情况,因为比如偶数x,它最近只可能是从x/2过来,不可能从左或者右走一步过来。
如图
从x/2到x只用了一步,如果是从x-1来的(x+1也同理),那一个奇数必然是从x-2来的,而x-2怎么来的一种是一步一步走,这个没啥好说的,另一种就是x/2左边的一个数x/2-1乘2变为x-2过来的(右边也同理),再走2步到x,总共就是“减一”、“乘法2”、“右一步”、“右一步”,共4步。那又有个疑问,偶数不左一步右一步那要怎么走?看一个实际的例子↓
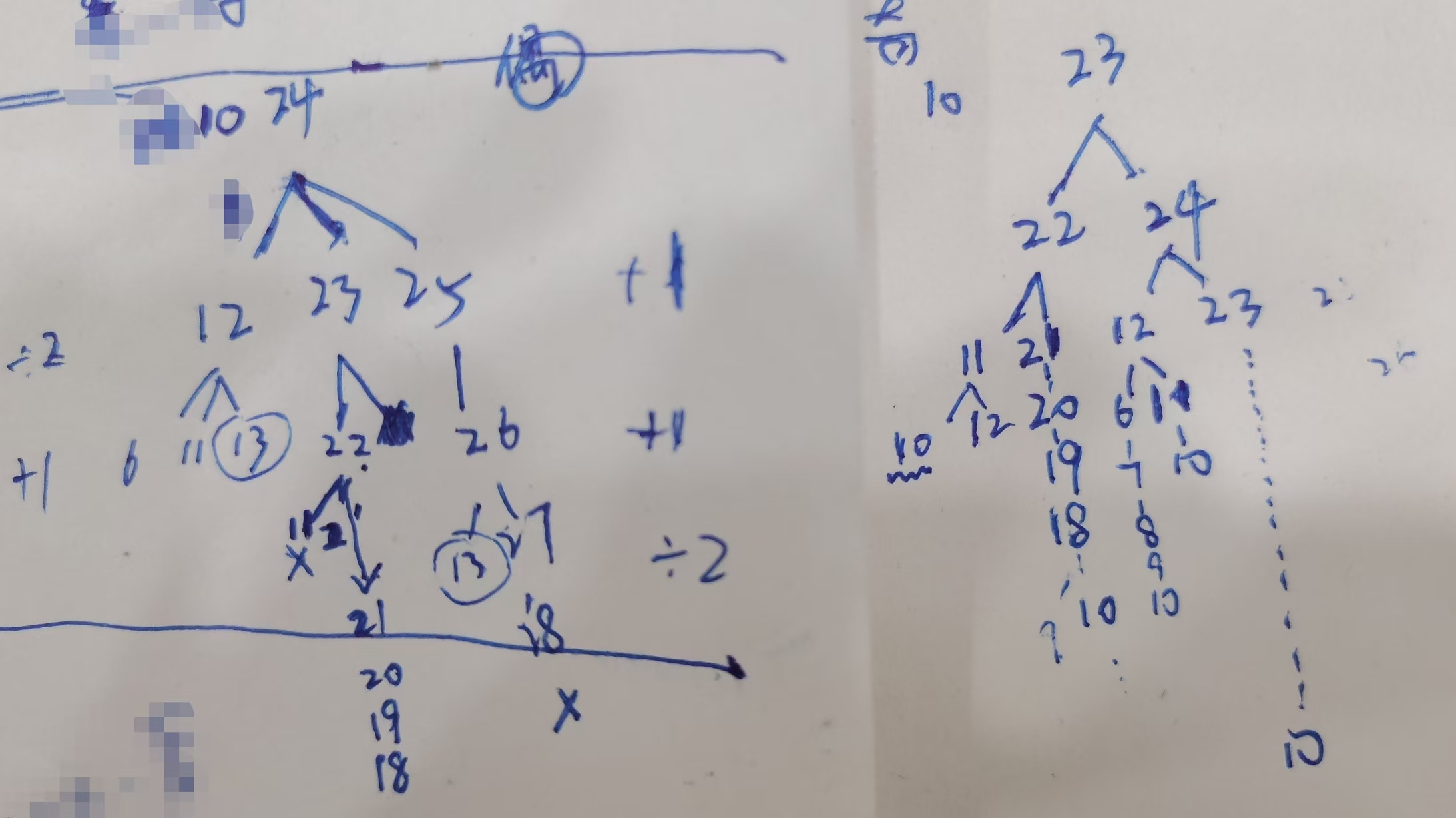
先看左边的例子10 24,24偶数看怎么走才能到10,显然最容易理解的从24到12,23,25,左枝12→6,11,13,中枝23→22,24(舍掉),右枝25→24(舍掉),26,6不用说了一步步倒退到10,11,13奇数先保留,22→11(舍弃),21,23(舍弃),舍弃11是因为“除以2再减1”两步就行了没必要减1再减1再除以2这样走3步,26→13,25(舍掉),27,现在剩下了保留的11,13,21,26走出来的13和27,先看27下一步是28,29......越走越远直接舍弃,所以24右枝整个都可以舍弃了,再来看26走出来的13,从24可以直接“÷2再+1”,两步到13,那为何还要“+1+1再整个÷2”呢?所以26走出来的13这枝也舍弃,现在只剩下保留的11,13,21,11按上面的思路也只有一步一步往前走到10,13,13→14,15,16.....越来越远舍弃,21也只有一步一步往回走到10。
综上,偶数只需要走2倍和一步一步退回n。
再来看奇数,右侧的23→22,24, 用上面的思路显然也就只有左一步右一步。
回过头看上面HEX9CF写的是最简洁的,编程大李子的代码有这段描述:

其中如果t为奇数(t变量真的很多余!直接用m就可以了),前一步后一步就好了,还一步步走啥?如果一步步向前真是最优解,那一定会包含在前一步过来这个算法里。经测试去掉此依旧AC
还有,如果t跑到了n前面(为了论证这句话没意义,长篇数学公式推导为了论证n - t 一定< t * 2 - n + 1,结果想太复杂了),也就是这句
return t * 2 - n + 1;
只要奶牛小于警察,就会直接返回,如果警察一步步走导致的小于那必然会先遇到奶牛直接返回,如果警察*2,或者奶牛÷2得到的奶牛小于警察,你为什么还要再判断一下“*2-n+1”,也就是奶牛÷2得到现在小于警察的位置,为啥还要再*2再跟n做差值,他本来就是从*2那个点过来的啊,如果那个点是做最优,直接-n就行了。而且“t*2”,t是奶牛,他不能*2,只能÷2。
但进一步思考,自己写的话不一定倒着走,也就是为啥要从奶牛÷2而不是警察*2呢?
想的很费劲,比如遇到13=13的时候,要算是恒等还是巧合,比如:x加1,乘2,减1,三步、x乘2,加1,两步骤,恒等。
这里奇数5可能走4→8→16→17也能走10→9→18→17,而如果为5 7,那又可以直接走5→6→7,所以奇数5可走左侧右侧二倍三种,而如果倒着走,会是奶牛÷2,奇数必然没这步骤,去掉很多不必要的路径,而可以看出时间复杂度为3^n,那编程大李子的代码为啥AC??就算这一句
return min(min(dfs(t+1)+1,dfs(t-1)+1),t-n);
也得2^n指数爆炸了,也不应该AC啊,之前acm时候记得1s是10^9,而2^30就10^9了
手动画出二叉树所有可能性感觉这个思路越来越像深搜和动态规划了(之前深搜广搜很好区分,现在感觉加上动态规划和递归他们仨都是一东西),之前看终止条件文章里的深搜代码的时候,一步步回,又觉得有点队列的思想。
回顾HEX9CF的代码,一步步递出去再回来,不回来的永远不知道哪是最优的,所以省去了深搜的剪枝判断step>minstep。
联想到hdoj11页的爬楼梯问题(递推/递归/动态规划/深搜?)
还有自己写的话没有if警察==0这句,提交后RE了,是死循环了,比如输入0 1,1的左判断到0,右判断到2,2的左判断走1→0(两步),右判断走1,如此看来1的右判断会2→1→2.........循环下去。
也就是0这个数没法乘2,那在他之前所有的探索都会被挡在外面,到最接近0的时候即1,1比较左右两个支,0和2,而2左支是一步步走到0,右支是÷2=1,奇数1的左支要跟右支偶数2比较,右支的偶数2的右支÷2永远到不了0,则死循环。
queue C++队列STL
poj从23号就开始挂了,28号还没好,看了下贴吧,放弃poj,此题提交的没返回结果,先搁置,感觉会TLE,加了个走过的标记vis,转洛谷OJ
POJ3278:2s 64M
洛谷p1588: 1s 125M 涉及POJ的题目在洛谷上提交会有提示,拉取自原OJ平台,这道题是洛谷自己有全部数据,不牵扯POJ
HDOJ2717:2s 32M

1 #include <iostream> 2 using namespace std; 3 #include<queue> 4 int vis[100050];//没有这个可能会超时 5 struct node 6 { 7 int x; 8 int step; 9 }; 10 queue<node>q; 11 int main() 12 { 13 int N, K; 14 cin >> N >> K; 15 vis[N] = 1; 16 node a; 17 a.x= N; 18 a.step =0; 19 q.push(a); 20 while(!q.empty()) 21 { 22 node next = q.front(); 23 node thisnode; 24 if(next.x == K) 25 { 26 printf("%d\n", next.step); 27 break; 28 } 29 if(next.x - 1 >= 0 && !vis[next.x-1]) 30 { 31 thisnode.x = next.x-1; 32 thisnode.step = next.step+1; 33 q.push(thisnode); 34 vis[thisnode.x] = 1; 35 } 36 if(next.x + 1 <= 100000 && !vis[next.x + 1]) 37 { 38 thisnode.x= next.x+1; 39 thisnode.step=next.step+1; 40 q.push(thisnode); 41 vis[thisnode.x] = 1; 42 } 43 if(next.x * 2 <= 100000 && !vis[next.x * 2]) 44 { 45 thisnode.x=next.x*2; 46 thisnode.step=next.step+1; 47 q.push(thisnode); 48 vis[thisnode.x] = 1; 49 } 50 q.pop(); 51 } 52 }
参考博客 省去了一个vis变量,很巧妙

1 #include <iostream> 2 using namespace std; 3 #include<queue> 4 int vis[100050];//没有这个可能会超时 5 struct node 6 { 7 int x; 8 int step; 9 }; 10 queue<node>q; 11 int main() 12 { 13 int N, K, t; 14 cin >> t; 15 while(t) 16 { 17 t--; 18 cin >> N >> K; 19 vis[N] = 1; 20 node a; 21 a.x = N; 22 a.step = 0; 23 q.push(a); 24 while(!q.empty()) 25 { 26 node next = q.front(); 27 node thisnode; 28 if(next.x == K) 29 { 30 printf("%d\n", next.step); 31 break; 32 } 33 if(next.x - 1 >= 0 && !vis[next.x - 1]) 34 { 35 thisnode.x = next.x - 1; 36 thisnode.step = next.step + 1; 37 q.push(thisnode); 38 vis[thisnode.x] = 1; 39 } 40 if(next.x + 1 <= 100000 && !vis[next.x + 1]) 41 { 42 thisnode.x = next.x + 1; 43 thisnode.step = next.step + 1; 44 q.push(thisnode); 45 vis[thisnode.x] = 1; 46 } 47 if(next.x * 2 <= 100000 && !vis[next.x * 2]) 48 { 49 thisnode.x = next.x * 2; 50 thisnode.step = next.step + 1; 51 q.push(thisnode); 52 vis[thisnode.x] = 1; 53 } 54 q.pop(); 55 } 56 } 57 }
在 node next = q.front(); 后加了行 printf("#%d\n",next.x);
发现没清空队列(清空没有clear的用法),输入1 2的时候,2满足条件直接break了没弹出在还在队列里,输入2 4后第一个#2是上一个1 2输出那个2,step为1,第二个#2是输入的2刚进队,step为0,但不冲突也不会覆盖,但为时已晚,#3#4是第一个#2弹出后进去的,step自然就是2了,于是加了 while(!q.empty()) q.pop();
但依旧WA
发现是没memset重置vis,
2 1 2 1 5 17 4 正确但输入 2 1 2 1 1 2 不输出
涉及上一次附近的数就有问题,在node next = q.front();前面加了句printf("##");,发现没进入while里的任何if语句,就q.pop了,为啥?那就是+1-1*2都没有能进的啊,为啥?因为都是vis等于1呀
加了memsetAC了
AC代码
1 #include <iostream> 2 #include<cstring> 3 using namespace std; 4 #include<queue> 5 int vis[100050];//没有这个可能会超时 6 struct node 7 { 8 int x; 9 int step; 10 }; 11 queue<node>q; 12 int main() 13 { 14 int N, K, t; 15 cin >> t; 16 while(t) 17 { 18 t--; 19 memset(vis,0,sizeof vis); 20 cin >> N >> K; 21 vis[N] = 1; 22 node a; 23 a.x = N; 24 a.step = 0; 25 q.push(a); 26 while(!q.empty()) 27 { 28 // printf("##"); 29 node next = q.front(); 30 // printf("#%d\n",next.x); 31 node thisnode; 32 if(next.x == K) 33 { 34 printf("%d\n", next.step); 35 while(!q.empty()) 36 q.pop(); 37 // printf("**%d\n", t); 38 break; 39 40 } 41 if(next.x - 1 >= 0 && !vis[next.x - 1]) 42 { 43 thisnode.x = next.x - 1; 44 thisnode.step = next.step + 1; 45 q.push(thisnode); 46 vis[thisnode.x] = 1; 47 } 48 if(next.x + 1 <= 100000 && !vis[next.x + 1]) 49 { 50 thisnode.x = next.x + 1; 51 thisnode.step = next.step + 1; 52 q.push(thisnode); 53 vis[thisnode.x] = 1; 54 } 55 if(next.x * 2 <= 100000 && !vis[next.x * 2]) 56 { 57 thisnode.x = next.x * 2; 58 thisnode.step = next.step + 1; 59 q.push(thisnode); 60 vis[thisnode.x] = 1; 61 } 62 q.pop(); 63 } 64 } 65 }
又思考,vis到底有没有必要,其实不加vis不会WA,因为首先不是动归,不会出现最后的某个加进来会比之前不取最大棒好的情况,比如背包问题,前面都拿最棒的拿后面没空间了,而如果少拿点,最后一个能放进去反而是最优的,而这里每一步都是1,不会出现翻盘的情况,所以此步最优即可,那也就没必要记录vis,因为哪怕路径绕远也不是覆盖,只是又填进队列里,真正正确的路径找到早就输出break了,所以不加vis不是会输出有误而是会超时,或者超内存,这里不对拍验证了。
洛谷提交1.1s,125M,但报错MLE内存超,好吧。
hdoj2717提交忘记了hdoj的EOF输入格式,WA了一次,现在已经搜不到友好的hdoj输入标准的解答了,过了那个时间段也就找不到了,不浪费时间,直接根据回忆写(知乎应该有使用教程当时也教过很多人使用11页和刷题线路)
AC代码
1 #include <iostream> 2 #include<cstring> 3 using namespace std; 4 #include<queue> 5 int vis[100050]; 6 struct node 7 { 8 int x; 9 int step; 10 }; 11 queue<node>q; 12 int main() 13 { 14 int N, K, t; 15 while(cin >> N >> K) 16 { 17 memset(vis, 0, sizeof vis); 18 vis[N] = 1; 19 node a; 20 a.x = N; 21 a.step = 0; 22 q.push(a); 23 while(!q.empty()) 24 { 25 node next = q.front(); 26 node thisnode; 27 if(next.x == K) 28 { 29 printf("%d\n", next.step); 30 while(!q.empty()) 31 q.pop(); 32 break; 33 34 } 35 if(next.x - 1 >= 0 && !vis[next.x - 1]) 36 { 37 thisnode.x = next.x - 1; 38 thisnode.step = next.step + 1; 39 q.push(thisnode); 40 vis[thisnode.x] = 1; 41 } 42 if(next.x + 1 <= 100000 && !vis[next.x + 1]) 43 { 44 thisnode.x = next.x + 1; 45 thisnode.step = next.step + 1; 46 q.push(thisnode); 47 vis[thisnode.x] = 1; 48 } 49 if(next.x * 2 <= 100000 && !vis[next.x * 2]) 50 { 51 thisnode.x = next.x * 2; 52 thisnode.step = next.step + 1; 53 q.push(thisnode); 54 vis[thisnode.x] = 1; 55 } 56 q.pop(); 57 58 } 59 } 60 }
备注:(回顾基础知识)
#曾经的代码网站也没法免费用了
#codeblock只要不是关闭重新打开,ctrlZ撤销可以存住所有修改记录
#上面的printf里的*%d只是将输出变为“*5”,意义与“!5、#5”都是一样的,为了区别开,看看是哪条printf输出,与指针毫无干系
#if进去了,下面的else if不会进
#嵌套函数return了不会跳出函数,只归回递它的上级。输出嵌套函数返回值不是终止条件return的
#回顾练习,包涵实参形参和全局变量、i++,++i,p++,++p问题(return和pritnf)

1 代码一: 2 int main() 3 { 4 int p; 5 int a[10]= {1,2,3,4,5,6}; 6 printf("%d %d %d\n", a[0], a[1], a[2]); 7 printf("p:%d\n", p); 8 printf("%d\n", a[++p]); 9 printf("p: %d\n", p); 10 printf("++p:%d\n", ++p); 11 printf("p:%d\n", p); 12 printf("p++:%d\n", p++); 13 printf("p:%d\n", p); 14 } 15 16 代码二: 17 #include<stdio.h> 18 int m=12; 19 int f() 20 { 21 return m++; 22 } 23 int main() 24 { 25 f(); 26 printf("%d\n", m); 27 } 28 //输出13

1 #include<stdio.h> 2 struct stu 3 { 4 char name[20]={'u'}; 5 int x; 6 int y; 7 }; 8 struct stu student;//[10]; 9 int main() 10 { 11 student.x = 10; 12 student.y = 120; 13 student.name[20] = 't'; 14 printf("%c\n", student.name[20]); 15 } 16 17 18 //#include<stdio.h> 19 //struct stu 20 //{ 21 // char name[20]; 22 // int x; 23 // int y; 24 //}; 25 //struct stu student;//[10]; 26 //int main() 27 //{ 28 // student.x = 10; 29 // student.y = 120; 30 // student.name[20] = 't'; 31 // printf("%c\n", student.name); 32 //}
字符数组赋值有问题,后面再弄
#一个变量进行递归的时候,进入某一层就变了,回来不会再变回去,除非是函数内的参数,输入1,输出#18,19

1 #include<stdio.h> 2 int N; 3 void fn(int x) 4 { 5 int q = 18; 6 if(x == 2){ 7 printf("#%d\n", q); 8 return; 9 10 } 11 else 12 { 13 q ++; 14 fn(x + 1); 15 printf("%d\n", q); 16 } 17 } 18 int main() 19 { 20 scanf("%d", &N);//1 21 fn(N); 22 }
下面全局变量,输入1,输出19,19

1 #include<stdio.h> 2 int N; 3 int q=18; 4 void fn(int x) 5 { 6 if(x == 2){ 7 q++; 8 printf("#%d\n", q); 9 return; 10 11 } 12 else 13 { 14 fn(x + 1); 15 printf("%d\n", q); 16 } 17 } 18 int main() 19 { 20 scanf("%d", &N);//1 21 fn(N); 22 }
所以DFS只用把步数用在函数内,作为函数内的参数
比如:
8 15
7 9 16 step: 1
6 14 10 18 15 17 32 step: 2
输入8 15,7,9,16进队列,step是1,7出来6,14进去,step是2,这时候队列是9,16,6,14,该9出来了,此时无论step当初设置的是全局还是局部变量,此时都已经是2了,+1是3,可9应该用最初的8 15的step+1,即0+1是1。
(其实可以再剪枝直接判断是不是想要的,是直接break输出,经测验poj的运行时间没影响)
#发现.cpp后缀的文件判断更严格,里面的int函数无int返回值会报警告
warning: no return statement in function returning non-void [-Wreturn-type]|
但.c后缀文件里的int函数无int返回值不会报警告,至于输出什么就是另一个需要研究的问题了(先搁置)。
#写了多种if else最后总结为只有三种,多的滑动博客文章都卡了

1 二: 2 if 3 else 4 { 5 if 6 } 7 8 三: 9 if 10 if flag 11 12 四: 13 if 14 else if
#洛谷比poj好太多了,题解、思路讨论、判题速度、分类、优质文章,就是略幼,毕竟中学生的东西,可能北大oj都是大佬写的简略交流我看不懂,但中学生全心全意纯粹的搞oi,确实比大学生强,放弃poj,从23号甚至更早崩溃到27号现在还没好
#这下还算有点点吃透了,还有好多疑惑问题没解决
#希望逐渐简化博客长度
#L雪T:“你不仅让我知道哪里错了,还知道为什么”,19考研的和他的日子只有回忆,tim/qq估计都没了。夏天群帮武理找bug找出个数据他不过。帮北邮一枝梅刷oj做平衡车他们大会神经网络
#洛谷从灰名→蓝名了,提交1588后
#发现之前自己写的代码真烂,强迫症强行想看懂,结果发现很多没必要的写法,数组没必要开2*10^5,且70行的return就很奇怪,说明那时候根本对搜索不透彻,这写法劳民伤财,这个return就相当于清空队列了,一步步return,真想看看之前那时候其他BFS是不是也都这么写的,点开这文章里的参考博客发现当时自己int/void函数涉及return的事都没搞清楚,return啥都会直接结束。这个人main里清空队列了也可以AC。poj单个数据数据导致养成了不好的习惯,洛谷和hdoj都很严谨,输入多组数据。就像上面开头pojAC代码hdojWA一样。
#垃圾百度输入着东西,没输完,就自动搜索跳到热搜广告,搜索东西那个AI智能搜索就不停加载导致页面一直向下动,想关闭还得等Ai搜索搜出来再关闭,AI搜索出来还很慢,真是傻逼,以后用必应,必应知识,函数遇到return返回,由于main是系统调用的,所以直接结束。

1 #include<stdio.h> 2 int main() 3 { 4 return 1; 5 // return 0; 6 // return 10; 7 printf("15\n"); 8 }
#写代码不要轻易看题解,容易思维定式,不是想破脑袋想出来的,直接得到的,很多地方坑点注意不到,也没有发散思维想那么多,最后稍微变个样就不会了
#这个文章里其实不用把我代码里的step也memset一遍,严谨点更好,但就像pdd买数码用品一样,知道原理逻辑就不会因为便宜而被骗反而还会省钱,理论上vis清空了,那为0的时候会再重新赋值
#scanf用EOF,先了解到这,scanf返回输入个数。cin不能用EOF,cin是流,返回值不可用'!','='运算符来比较。百度唯一比必应好用的就是编译器有报错信息时候,复制到百度那个它的智能回答比必应要好

1 #include<stdio.h> 2 int main() 3 { 4 int m,n; 5 printf("%d", scanf("%d %d", &m, &n));//scanf返回输入数据个数 6 }

1 #include<iostream> 2 using namespace std;//cin定义在命名空间中,没有这句不行 3 int main() 4 { 5 int m,n; 6 while(cin>>m>>n) 7 // while((cin>>m>>n) != 0)//EOF也不对,cin是一个流,不支持用!=比较 8 // printf("%d", cin>>m>>n));//报错 9 } 10 //EOF通常是-1
#C++的cin/cout、STL命名空间、命名空间、为什么C++需要使用命名空间(想用cout只用iostream报错,必须再加个using namespace std)
#回顾这些斜枝末节的基础真的好耽误时间 while语句中的continue和break、洛谷题解讨论(也用了巧妙的省去vis开销的方法) while循环中return/break/continue的区别、取地址符形参实参
测试(形参实参和全局变量不同)

1 #include<stdio.h> 2 #include<string.h> 3 int a; 4 int b; 5 int F1(int x) 6 { 7 x=11;; 8 } 9 void F2() 10 { 11 b=11;; 12 } 13 14 int main() 15 { 16 a=1; 17 b=1; 18 F1(a); 19 printf("%d\n",a); 20 F2(); 21 printf("%d\n",b); 22 }
#




 浙公网安备 33010602011771号
浙公网安备 33010602011771号