CCF 无线网络
题目原文
| 试题编号: | 201403-4 |
| 试题名称: | 无线网络 |
| 时间限制: | 1.0s |
| 内存限制: | 256.0MB |
| 问题描述: |
问题描述
目前在一个很大的平面房间里有 n 个无线路由器,每个无线路由器都固定在某个点上。任何两个无线路由器只要距离不超过 r 就能互相建立网络连接。
除此以外,另有 m 个可以摆放无线路由器的位置。你可以在这些位置中选择至多 k 个增设新的路由器。 你的目标是使得第 1 个路由器和第 2 个路由器之间的网络连接经过尽量少的中转路由器。请问在最优方案下中转路由器的最少个数是多少? 输入格式
第一行包含四个正整数 n,m,k,r。(2 ≤ n ≤ 100,1 ≤ k ≤ m ≤ 100, 1 ≤ r ≤ 108)。
接下来 n 行,每行包含两个整数 xi 和 yi,表示一个已经放置好的无线 路由器在 (xi, yi) 点处。输入数据保证第 1 和第 2 个路由器在仅有这 n 个路由器的情况下已经可以互 相连接(经过一系列的中转路由器)。 接下来 m 行,每行包含两个整数 xi 和 yi,表示 (xi, yi) 点处可以增设 一个路由器。 输入中所有的坐标的绝对值不超过 108,保证输入中的坐标各不相同。 输出格式
输出只有一个数,即在指定的位置中增设 k 个路由器后,从第 1 个路 由器到第 2 个路由器最少经过的中转路由器的个数。
样例输入
5 3 1 3
0 0 5 5 0 3 0 5 3 5 3 3 4 4 3 0 样例输出
2
|
题目大意
给你n个点,随后给出的每个点的坐标,再给你m个候选点,从m个候选点中选择最多k个点作为新增设的点。给定数值r作为一个点可到达另一个点的最远距离(可以等于)。现让你计算出从起始坐标(坐标点从0算起,第0个点为起始坐标)到终点坐标(第1个点)最少需要经历多少个点(可以有新增设的点,但不能超过k个)。
题目思路
权值均为1的SPFA。设置一个dec_[205][105]数组,dec_[i][k]表示经过了k个新增设的点到达第i个点最短距离是多少。采用SPFA思想(并不是BFS)。
举一组数据:(应该输出10)
10 4 2 1
0 0
5 0
0 1
0 2
0 3
1 3
3 0
3 1
3 2
3 3
1 0
2 0
2 3
4 0
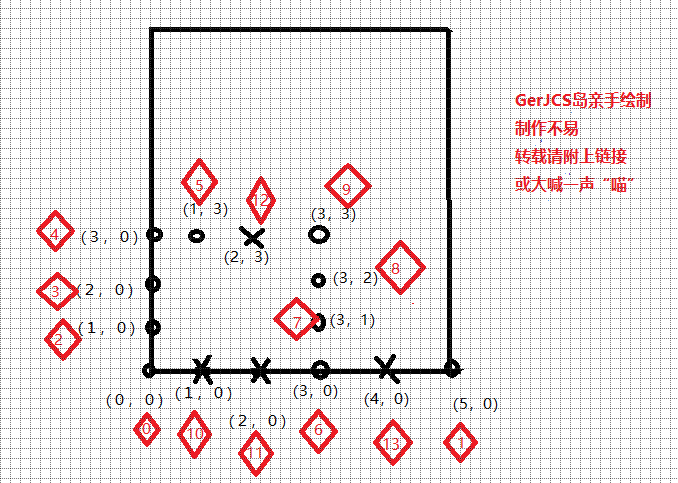
仔细看一下数据和图解,绘制很辛苦,如果这个题思考很久没思路其他题解看不懂就用心看我这个,很详细。
前面和bfs一样,后面类似动态选择一样,这也是SPFA的特点,不是每个距离够的相邻点都能进入队列,成为下一个可走节点,而是还要判断是否需要松弛,松弛什么意思我也不懂,SPFA里,距离更近的赋值给我就说成是松弛。
对每一个dec_数组都设置成int最大数值,有现成函数INT_MAX。(这题可以这样写,但是一般不设置为INT_MAX,因为如果涉及到值为INT_MAX这个数据的变量,一旦加数字就会为负数,所以一般根据情况,减10)
对于一个轴点willpush(含有x,y,i,k的结构体,willpush.x和y表示坐标,willpush.i表示该点在n个点中是第几个点,willpush.k表示经过了几个新增设的点到达这里),遍历所有 非此点/非终点 的点(遍历变量 i ),如果可走,则到达点 i ,经过mid_k(记录经过k的个数,如果是”ד,就+1)个新增设点的dec_[i][mid_k]和到达轴点willpush.i的点经过willpush.k个新增设点的dec_[willpush.i][willpush.k] 加一,比较
1 if(dec_[i][mid_k] > dec_[willpush.i][willpush.k] + 1){ 2 dec_[i][mid_k] = dec_[willpush.i][willpush.k] + 1;
就是说,轴点记录从起点到达当前点这里,经过k个(当然k可以有多个)新增设点所需要的最少步数dec_(这里说位步数是因为权值位1,从一个点到达下一个点就是一步),那就以我为中心,向周围找一圈,比如遇到第一个可走的点(距离r内),这里先叫它node吧,那以我这个最短距离dec_再加一作为到达node这里(经过了经历的k个新增设点)理应最小的数值,然后与实际存的dec_数值作比较。
用那个栗子说一下就明白了,

圆圈表示点,“×”表示新增设的点,菱形里面的数字代表作为第几个点输入的,以下用“菱形+数字”代表第几个点。
首先从
◆0出发,◆10 and ◆2 入队列,
◆2出队列,◆3入队列,◆10出队列,◆11入队列。
到这里为止先分析一下数据,每一次入队列之前的dec_都需要改变,比如以◆0作为轴点向四周遍历的时候,◆2可走,简单比价dec_赋值为1,◆10入队的时候,发现这个点dec_[10][1]初始值位INT_MAX最大值,即第10个输入的点,经历1个新增设点到达的位置目前最短距离位INT_MAX,我与◆0的dec_[0][0](初始值只有这个设置为0)加一作比较,即“1”与INT_MAX作比较,小于,则赋值(松弛),现在dec_[10][1]是 1了。接着继续......
◆3出,◆4入,◆11出,◆6入。
到这里埋一个伏笔,很重要也是dec_的精髓,和本题的巧妙思维所在(我自己没先到,看了题解有吭哧瘪肚看了好几天)
◆4出,◆5入,◆6出,◆13入不了!只能入◆7,因为k给定是2,最大新增设的点为两个。再继续......
◆5出,◆12入,◆7出,◆8入。
◆12出,◆9入,◆8出,◆9入。
◆9出,◆8入
到这里再埋下一个伏笔,作为第二个伏笔
◆8出,◆7入,◆7出,◆6入。
到这里结合第一个伏笔解释,第一个伏笔◆6入的时候,存入的dec_值仔细想想再看下面答案
值应该为dec_[6][2],最后赋值成从◆11来的加一,即走3步最短到这里,而这里的◆6入要分清怎么来的,区别于第一次◆6入。第一次◆6入后只能向上走,走◆7,走◆8走◆9,到了◆9就不能走◆12了,也不能回到◆8 了 ,因为同样是走两个新增设的k点,到◆8,到◆9就不能再回◆8了因为if判断那里距离不是更近,所以不压入队列。这也就顺便解释了第二个伏笔。
这里的第二次◆6入其实是从◆2,◆3,◆4,◆5,◆12,◆9,◆8,◆7到的◆6,体现dec_精华巧妙地地方来了,第一次的◆6入是从下面◆0,◆10,◆11走到的,dec_[6][2]值为3,而向右堵住了,向上又没回来卡再在◆9,只能凑够◆2,◆3,◆4,◆5,◆12,◆9,◆8,◆7到的◆6,那么dec_是怎样的呢?思考不出来或者已经会了再看答案
答案其实是dec_[6][1]值为9,经过一个新增设的点到达◆6,最短需要9步。这里巧妙在于没有把 ◆6“最短距离”写死,用了一个二维数组记录不同路径到达这个点的不同最小值,这里的不同路径主要就在于这些新增设的点。而不至于想我一开始写的似得,◆0,◆10,◆11,◆6再往右走不了,从◆2,◆3,◆4,◆5,◆12,◆9,◆8,◆7到◆6的数值因为没有之前◆6存的数小而不入队,导致卡死这里了。或者我这个◆2,◆3,◆4,◆5,◆12,◆9,◆8,◆7到◆6依然是3就麻烦了。相当于走的一大圈回来应该是你一大圈的路程,却偷了之前短的数据。
(这里比较不好解释,多写然后printf找出问题所在,实在理解不了,加我微信acmer13936130136我给你讲一下吧,备注“博客园来的,询问CCF无线网络题目”加好后主动发我这篇博客链接)。希望每一个人都能A掉这个题目。我自己写完都未必能重写满分或者思路尤在,更别说面试考这个了,再加油吧!
注意:1.涉及到r运算的地方,要设置为long long int,否则整型只有80分
2.不能设置visit走过则不入队的数组,否则也死,还拿◆6举例子,自己想一下吧,不会加微信问。
AC代码

1 #include<cstdio> 2 #include<climits> 3 #include<cstring> 4 #include<queue> 5 #include <iostream> 6 #include <algorithm> 7 using namespace std; 8 struct node 9 { 10 int x; 11 int y; 12 int i; 13 int k; 14 }map[205]; 15 int n, m, k; 16 long long int r; 17 int Sx, Sy; 18 int Tx, Ty; 19 int SPFA(int i); 20 bool legal(long long int Ax, long long int Bx, long long int Ay, long long int By); 21 int dec_[205][105]; 22 int main() 23 { 24 scanf("%d %d %d %lld", &n, &m, &k, &r); 25 for(int i = 0; i < n + m; i ++) 26 scanf("%d %d", &map[i].x, &map[i].y); 27 for(int i = 0; i < 201; i ++) 28 for(int j = 0; j < 101; j ++) 29 dec_[i][j] = INT_MAX; 30 dec_[0][0] = 0; 31 Sx = map[0].x; 32 Sy = map[0].y; 33 Tx = map[1].x; 34 Ty = map[1].y; 35 printf("%d\n", SPFA(0)); 36 } 37 bool legal(long long int Ax, long long int Bx, long long int Ay, long long int By) 38 { 39 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 40 return true; 41 else 42 return false; 43 } 44 int SPFA(int i) 45 { 46 queue<node> s; 47 node mid;//中转 48 node willpush;//即将压入 49 node next; 50 mid.x = Sx; 51 mid.y = Sy; 52 mid.i = 0; 53 mid.k = 0; 54 s.push(mid); 55 int mid_k; 56 while(!s.empty()){ 57 willpush = s.front(); 58 s.pop(); 59 for(int i = 0; i < n + m; i ++){ 60 if(legal(willpush.x, map[i].x, willpush.y, map[i].y)) 61 { 62 if(willpush.x == map[i].x && willpush.y == map[i].y) 63 continue; 64 if(map[i].x == Tx && map[i].y == Ty) 65 return dec_[willpush.i][willpush.k];//这些个坐标,变量很有讲究 66 mid_k = willpush.k; 67 if(i >= n){ 68 if(willpush.k == k) 69 continue; 70 mid_k = willpush.k + 1; 71 } 72 if(dec_[i][mid_k] > dec_[willpush.i][willpush.k] + 1){ 73 dec_[i][mid_k] = dec_[willpush.i][willpush.k] + 1; 74 next.x = map[i].x; 75 next.y = map[i].y;//调试好久。。。。 76 next.i = i; 77 next.k = mid_k; 78 s.push(next); 79 } 80 } 81 } 82 } 83 return 0; 84 } 85 86 //5 3 1 3 87 //0 0 88 //5 5 89 //0 3 90 //0 5 91 //3 5 92 //3 3 93 //4 4 94 //3 0 95 96 //10 4 2 1 97 //0 0 98 //5 0 99 //0 1 100 //0 2 101 //0 3 102 //1 3 103 //3 0 104 //3 1 105 //3 2 106 //3 3 107 //1 0 108 //2 0 109 //2 3 110 //4 0
PS:本题目数据应该是有点水,因为如果把68/69行去掉,也是可以AC的,只不过30ms
按理说应该遇到更多的新增设点返回不做数的,这里后台测试数据应该是没有给出一条可以超过k的路径走法。
这里我参考了很多题解才看懂,看题解过程中无意间看到一组数据就是我上面的那个例子(来源于这题解下面的评论(不过这链接里的两代码都是错误的,尽管CCF可以AC,我的那个例子和链接里的评论就是反例,所有BFS写的都是如此,都是错误的))其实应该晚一点看到的,不然先入正确思路会错过很多坑,这样下面写其他题目的时候还会出错)
附录:
看到题目我没什么思路,感觉想搜索。
简单想一下,我最先想到的是想用DFS,先将k,r变一下表述,38,40行容易理解。7行的变量为是否为非新增设的点,即是否是本身就有的点。8行变量为新增设的点。我是想深搜,从起点开始,搜出所有的可走路径,对于每一个点我一开始误以为都是r为3,错误的将走步设置为3之内,即最多上下左右走2格。对于可以走的(r之内,边界之内),(我的63行写错了,实际想表达。对意思是这个点是否为n个点面的,if(is_be_point[map[i][0]][map[i][1]] == 1) ,或者m点里未超过k的),是就压入DFS递归再以这个点继续。最后用answer数组记录所有可以到达终点的路径值,取min。
但是有几个问题:
1.数组开不了10^8。而如果这一步:判断该点是否是n个内的点,应该for(0 < i < n)判断thisx,thisy是否与(x,y)匹配,即当前点存在于map数组内。(map数组记录的是n个的,can_be_set记录的是m个的)。或者set什么vetor之类的容器?判断是否在此坐标数据中出现过?感觉考的不是这个知识,而且这么写很蠢,多半会超时。
2.路径太多了,可能超时。因为走过还可以走,类似dp动态规划,即走这一步不一定是最优的(新增设点的存在),有可能无穷多条。即
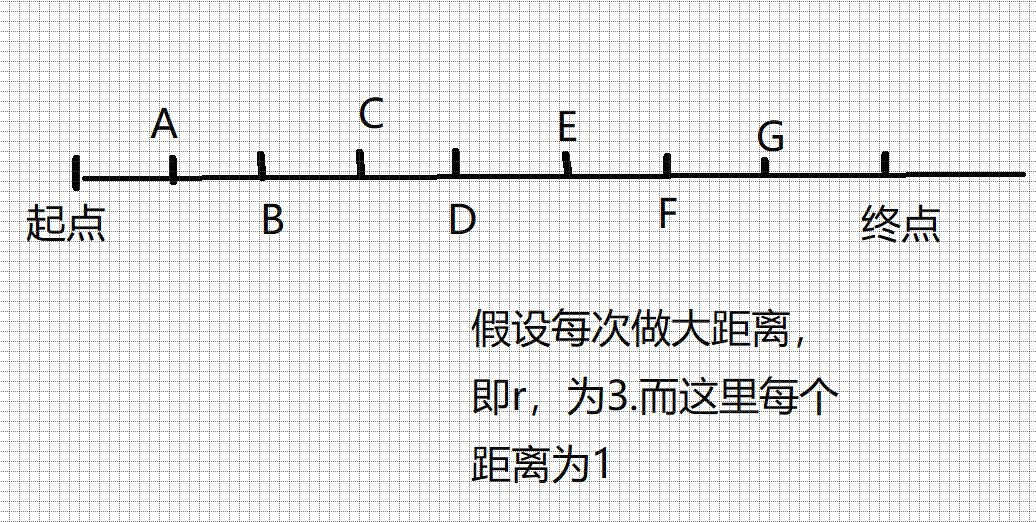
我可以起点→A→B→C→D→E......终点、起点→B→C→D→E......终点、起点→ C→D→E......终点、起点→B→D→E......终点。
可见对于一条路径几乎就有无穷中变数走法,类似贪心和动态规划。
正常搜索是没有“跳着”的,都是“一步一个脚印”,距离够(一般都是1,格子嘛)就走,除非遇到了非法格子地图外,或者有路径先到达,否则一直一步一步走着。可这个感觉怪怪的,像贪心和动态规划。只考虑r无形中就增加好多路径,还没考虑k的事呢,感觉这法子不行。
有同学说,那我每次最大格子走呢,即走小于r最大整数。我举一个反例

r还是3,k是1,k最多就可以添加一个。
那我从起点到达第一个×,接着下一步跨3个格子,再接着一步跨3个格子就到了第二个新增设点“×”,那只能返回重新选择走法,很像动态规划。
3.思路本身就不对
写崩了的代码......
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 5 int n, m, k, r; 6 int map[105][2]; 7 int is_be_point[100000000][100000000]; 8 int can_be_set[105][2]; 9 void dfs(int x, int y); 10 11 int dec[28][2] = 12 {{0, -1}, {0, -2}, {0, -3}, {0, 1}, {0, 2}, {0, 3},//横 13 {-1, 0}, {-2, 0}, {-3, 0}, {1, 0}, {2, 0}, {3, 0},//竖 14 {-2, 1}, {-2, 2}, {-2, -1}, {-2, -2}, {-1, 1}, {-1, 2}, {-1, -1}, {-1, -2}, 15 {2, 1}, {2, 2}, {2, -1}, {2, -2}, {1, -1}, {1, -2}, {1, 1}, {1, 2} }; 16 17 int Sx, Sy, Tx, Ty; 18 int max_number_can_set; 19 int max_can_dec; 20 bool legal(int x, int y); 21 int main() 22 { 23 scanf("%d %d %d %d", &n, &m, &k, &r); 24 for(int i = 0; i < n; i ++){ 25 scanf("%d %d", &map[i][0], &map[i][1]); 26 is_be_point[map[i][0]][map[i][1]] = 1; 27 if(i == 0) 28 { 29 Sx = map[i][0]; 30 Sy = map[i][1]; 31 } 32 if(i == 1) 33 { 34 Tx = map[i][0]; 35 Ty = map[i][1]; 36 } 37 } 38 max_number_can_set = k; 39 max_can_dec = r; 40 for(int i = 0; i < m; i ++){ 41 scanf("%d %d", &can_be_set[i][0], &can_be_set[i][1]); 42 43 } 44 // 思考DFS还是BFS 45 dfs(Sx, Sy); 46 } 47 bool legal(int x, int y) 48 { 49 // if(abs(x) <= abs(Sx) && x <= Tx && y <= Ty && abs(y) <= Sy)//略有不同。。。好难写啊 50 if(x < max(Sx, Tx) && x > min(Sx, Tx) && 51 y < max(Sy, Ty) && y > min(Sy, Ty)) 52 return true; 53 else 54 return false; 55 } 56 void dfs(int x, int y) 57 { 58 if(!legal(x, y)) 59 return; 60 for(int i = 0; i < 29; i ++){ 61 int thisx = x + dec[i][0]; 62 int thisy = y + dec[i][1]; 63 if(map[thisx][thisy]) 64 dfs(thisx, thisy); 65 66 } 67 }
写的好烦🔥🔥🔥。。。代码好烦。🔥🔥🔥。。考研好烦。🔥🔥🔥。。时间好紧张、😠😠😠、。。何时才能心无旁骛的学习😠😠😠
我要年薪30w。😈😈😈。啊啊啊啊啊!!!😈😈😈
写过了DFS,试试BFS。
stl都不会,想手写C语言的数组表示的队列
1 #include<cstdio> 2 #include<climits> 3 #include<queue> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 //int map[205][2]; 8 struct node{ 9 int x; 10 int y; 11 int step; 12 int kcount; 13 } map[205]; 14 int n, m, k, r; 15 int Sx, Sy; 16 int Tx, Ty; 17 int SPFA(int i); 18 bool legal(int Ax, int Ay, int Bx, int By); 19 int main() 20 { 21 scanf("%d %d %d %d", &n, &m, &k, &r); 22 for(int i = 0; i < n + m; i ++){ 23 scanf("%d %d", &map[i].x, &map[i].y); 24 map[i].step = INT_MAX; 25 map[i].kcount = 0; 26 } 27 map[0].step = 0; 28 Sx = map[0].x; 29 Sy = map[0].y; 30 Tx = map[1].x; 31 Ty = map[1].y; 32 SPFA(0); 33 } 34 bool legal(int Ax, int Ay, int Bx, int By) 35 { 36 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 37 return true; 38 else 39 return false; 40 } 41 int SPFA(int i) 42 { 43 queue<node> s; 44 node p; 45 // s.x = Sx; 46 // s.y = Sy; 47 // s.push(map[0]); 48 p.x = Sx; 49 p.y = Sy; 50 s.push(p); 51 while(!s.empty()){ 52 p = s.front(); 53 s.pop(); 54 if(p.x == Tx && p.y == Ty) 55 return p.step; 56 for(int i = 0; i < n + m; i ++){ 57 if(i >= n && s.kcount == k) 58 continue; 59 if(legal(s.x, map[i].x, s,y, map[i].y)){ 60 if(i >= n){ 61 map[i].kcount = s.kcount ++; 62 } 63 s.push(map[i]); 64 if(map[i].step > s.step + 1) 65 map[i].step = s.step + 1; 66 } 67 } 68 } 69 }
代码有改动,但思路主要是BFS,这个思路问题主要出在没有搞清楚究竟怎样处理新增设点条件下的最短(这个题如果没有新增设点的条件就是最最简单基础的BFS)。具体位置是64/65行,
这里不应该这么比较,把距离作为该点的单一类似BFS里面的固有属性,某点目前最小值就用某一值来记录,
而是应该同时记录出是经历几个新增设的点到达这里的。
其他问题不说,就是这个引起的问题吧,拿这个举例子

我◆0→◆10→◆11→◆6是4步。而◆0→◆2→◆3→◆4→◆5→◆12→◆9→◆8→◆7→◆6是9步但是在64行依旧是最距离4,相当于偷换。或者说没比较出真是的距离。
我看了一下别人代码说SPFA,就写了一下。但错在了依旧是BFS的思路,依旧是64行那个错误。
1 ////#include<cstdio>
2 ////int map[205][2];
3 ////int n, m, k, r;
4 ////void SPFA();
5 ////int main()
6 ////{
7 //// scanf("%d %d %d %d", &n, &m, &k, &r);
8 //// for(int i = 0; i < n + m; i ++){
9 //// scanf("%d %d", &map[i][0], &map[i][1]);
10 //// if(i == 0){
11 //// Sx = map[i][0];
12 //// Sy = map[i][1];
13 //// }
14 //// if(i == 1)
15 //// {
16 //// Tx = map[i][0];
17 //// Ty = map[i][1];
18 //// }
19 //// }
20 //// SPFA(Sx, Sy);
21 ////}
22 ////bool legal(int Ax, int Ay, int Bx, int By)
23 ////{
24 //// if((Bx - Ax) * (Bx - Ax) + (By - Ay) * (By - Ay) <= r * r)
25 //// return true;
26 //// else
27 //// return false;
28 ////}
29 ////void SPFA()
30 ////{
31 //// for(int i = 0; i < n + m; i ++){
32 ////
33 //// }
34 ////}
35 //
36 //
37 ///* CCF201403-4 无线网络 */
38 //
39 //#include <iostream>
40 //#include <cstring>
41 //#include <queue>
42 //
43 //using namespace std;
44 //
45 //const int MAXN = 100 + 100;
46 //
47 //struct {
48 // long long x, y;
49 //} coord[MAXN+1];
50 //
51 //struct status {
52 // long long x, y;
53 // int step, kcount;
54 //};
55 //
56 //bool visited[MAXN+1];
57 //
58 //int dfs(int n, int m, int k, int begin, int end, long long r)
59 //{
60 // int max;
61 //
62 // // 变量初始化
63 // memset(visited, false, sizeof(visited));
64 //
65 // // 设置根结点
66 // status start, front, v;
67 // start.x = coord[begin].x;
68 // start.y = coord[begin].y;
69 // start.step = 0;
70 // start.kcount = 0;
71 // queue<status> q;
72 // q.push(start);
73 //
74 // // 设置根结点为已经访问过
75 // visited[begin] = true;
76 //
77 // while(!q.empty()) {
78 // front = q.front();
79 // q.pop();
80 //
81 // // 到达终点则结束
82 // if(front.x == coord[end].x && front.y == coord[end].y)
83 // return front.step - 1;
84 //
85 // // 搜索可以连接的路由器
86 // if(front.kcount == k)
87 // max = n;
88 // else
89 // max = n + m;
90 // for(int i=0; i<max; i++) {
91 // // 访问过的坐标则跳过
92 // if(visited[i])
93 // continue;
94 //
95 // // 判定下一个路由器的坐标是否在半径r之内, 不在半径之内则跳过,在半径之内则继续搜索
96 // if((front.x - coord[i].x) * (front.x - coord[i].x) + (front.y - coord[i].y) * (front.y - coord[i].y) > r * r)
97 // continue;
98 // else {
99 // // 第i个路由器设为已经访问过
100 // visited[i] = true;
101 //
102 // // 计算步数,并且将第i个路由器加入队列
103 // v.x = coord[i].x;
104 // v.y = coord[i].y;
105 // v.step = front.step + 1;
106 // if(i >= n)
107 // v.kcount = front.kcount + 1;
108 // else
109 // v.kcount = front.kcount;
110 // q.push(v);
111 // }
112 // }
113 // }
114 //
115 // return 0;
116 //}
117 //
118 //int main()
119 //{
120 // int n, m, k;
121 // long long r;
122 //
123 // // 输入数据
124 // cin >> n >> m >> k >> r;
125 // for(int i=0; i<n+m; i++) // n个路由器的位置+可以增设的m个路由器的位置
126 // cin >> coord[i].x >> coord[i].y;
127 //
128 // // BFS
129 // int ans = dfs(n, m, k, 0, 1, r);
130 //
131 // // 输出结果
132 // cout << ans << endl;
133 //
134 // return 0;
135 //}
136 //
137 ///*
138 //测试数据:
139 //5 3 1 3
140 //0 0
141 //5 5
142 //0 3
143 //0 5
144 //3 5
145 //3 3
146 //4 4
147 //3 0
148 //2
149 //10 1 1 2
150 //0 0
151 //3 1
152 //-2 0
153 //-2 2
154 //-2 4
155 //-2 6
156 //0 6
157 //2 6
158 //2 4
159 //2 2
160 //2 0
161 //1
162 //10 1 1 2
163 //0 0
164 //3 1
165 //-2 0
166 //-2 2
167 //-2 4
168 //-2 6
169 //0 6
170 //2 6
171 //2 4
172 //2 2
173 //3 0
174 //8
175 //6 3 2 50000000
176 //0 0
177 //50000000 100000000
178 //100000000 100000000
179 //100000000 0
180 //100000000 50000000
181 //50000000 0
182 //-100000000 50000000
183 //0 50000000
184 //0 100000000
185 //2
186 //*/
187 //
188 ////10 4 2 1
189 ////0 0
190 ////5 0
191 ////0 1
192 ////0 2
193 ////0 3
194 ////1 3
195 ////3 0
196 ////3 1
197 ////3 2
198 ////3 3
199 ////1 0
200 ////2 0
201 ////2 3
202 ////4 0
203
204 //#include<algorithm>
205 //#include<cstdio>
206 //#include<cstring>
207 //#include<iostream>
208 //#include<queue>
209 //#define N 205
210 //#define INF 0x3f3f3f3f
211 //typedef long long LL;
212 //using namespace std;
213 //
214 //struct P {
215 // int x,y;
216 //} p[N];
217 //
218 //
219 //int n,m,k,r;
220 //int d[N][N];
221 //bool vis[N][N],Map[N][N];
222 //
223 //void spfa() {
224 // queue<P> q;
225 // memset(vis,0,sizeof(vis));
226 // memset(d,INF,sizeof(d));
227 // //这里的d[i][j]和vis[i][j]有特殊的含义
228 // // d[i][j]表示从起点开始,经过增设的j个点,到达第i个点的最短路径
229 // // vis[i][j]表示是否可以从起点经过增设的j个路由器到达i
230 // d[0][0]=0;
231 // vis[0][0]=1;
232 // //这里的s和tem感觉已经不再是表示一个点了,所以有点错觉
233 // P s,tem;
234 // int des_p=0,ap_num=0;
235 // int tp_des_p,tp_ap_num;
236 // s.x=s.y=des_p;
237 // q.push(s);
238 // while(!q.empty()) {
239 // s=q.front();
240 // q.pop();
241 // des_p=s.x;
242 // ap_num=s.y;
243 // vis[des_p][ap_num]=0;
244 // for(int i=0; i<n+m; ++i)
245 // //和s点相连的点
246 // //另外看到这里莫名感觉这题简单(什么都不会,但有一种莫名的自信)
247 // //这哪是spfa啊,更像是普通的bfs(写完我就后悔了= =)
248 // //这里的s.x其实就是点的编号。程序可读性差= =(明明可以用别的表示的,非得图省事用P,差评!)
249 // //嗯……这个程序有点带劲啊╮(╯▽╰)╭
250 // if(Map[des_p][i]) {
251 // //下面这几句是重点啊
252 // tp_des_p=i;
253 // tp_ap_num=ap_num;
254 // if(i>=n) ++tp_ap_num;
255 // if(tp_ap_num<=k && d[tp_des_p][tp_ap_num]>d[des_p][ap_num]+1) {
256 // //只要符合以上条件就进行松弛
257 // d[tp_des_p][tp_ap_num]=d[des_p][ap_num]+1;
258 // //如果不在队列里就让其进入队列
259 // if(!vis[tp_des_p][tp_ap_num]) {
260 // vis[tp_des_p][tp_ap_num]=1;
261 // //进入队列的其实是起点所到目的地点和经过的增设点数
262 // tem.x=tp_des_p;
263 // tem.y=tp_ap_num;
264 // q.push(tem);
265 // }
266 // }
267 // }
268 // }
269 // int ans=INF;
270 // for(int i=0; i<=k; i++) ans=min(ans,d[1][i]);
271 // printf("%d\n",ans-1);
272 //}
273 //
274 //int main() {
275 // int i,j;
276 // cin>>n>>m>>k>>r;
277 // //输入存在的点和可以放置的点
278 // for(i=0; i<n+m; ++i) scanf("%d%d",&p[i].x,&p[i].y);
279 // //map是邻接矩阵
280 // memset(Map,0,sizeof(Map));
281 // //这个循环看起来不免重复,但是没超时
282 // for(i=0; i<n+m; ++i)
283 // for(j=i+1; j<n+m; ++j)
284 // //LL就是long long int,这里是强制类型转换
285 // if(LL(p[i].x-p[j].x)*(p[i].x-p[j].x)+LL(p[i].y-p[j].y)*(p[i].y-p[j].y)<=LL(r)*r)
286 // Map[i][j]=Map[j][i]=1;
287 //
288 // spfa();
289 // return 0;
290 //}
291
292
293
294
295 //先想好在写还是边写边想——后者
296 //参考 SPFA算法详解(强大图解,不会都难)
297 #include<cstdio>
298 #include<climits>
299 #include<queue>
300 #include <iostream>
301 #include <algorithm>
302 using namespace std;
303 //int map[205][2];
304 struct node{
305 int x;
306 int y;
307 int step;
308 int kcount;
309 } map[205];
310 //int queue[205];//出现绿色是用库还是?
311 int n, m, k, r;
312 int Sx, Sy;
313 int Tx, Ty;
314 int SPFA(int i);
315 bool legal(int Ax, int Ay, int Bx, int By);
316 int main()
317 {
318 scanf("%d %d %d %d", &n, &m, &k, &r);
319 for(int i = 0; i < n + m; i ++){
320 scanf("%d %d", &map[i].x, &map[i].y);
321 map[i].step = INT_MAX;
322 map[i].kcount = 0;
323 }
324 map[0].step = 0;
325 Sx = map[0].x;
326 Sy = map[0].y;
327 Tx = map[1].x;
328 Ty = map[1].y;
329 SPFA(0);
330 }
331 bool legal(int Ax, int Ay, int Bx, int By)
332 {
333 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r)
334 return true;
335 else
336 return false;
337 }
338 int SPFA(int i)
339 {
340 // queue[i ++] = Sx
341 queue<int> s;
342 node s;
343 node p;
344 s.x = Sx;
345 s.y = Sy;
346 s.push(map[0]);
347 while(!empty()){
348 p = s.front();
349 if(p.x == Tx && p.y == Ty)
350 return p.step;
351 for(int i = 0; i < n + m; i ++){
352 if(i >= n && s.kcount == k)
353 continue;
354 if(legal(s.x, map[i].x, s,y, map[i].y)){
355 if(i >= n){
356 map[i].kcount = s.kcount ++;
357 if()
358 }
359 push(map[i]);
360 if(map[i].step > s.step + 1)
361 map[i].step = s.step + 1;
362 }
363 }
364 }
365 }
我具体学了一下SPFA 参考博客
之前一战结束时刷pat时学过SPFA,所以一看就会了,只是调试写起来很劲。
第一次运行(依旧是64行的那个问题)
1 #include<cstdio> 2 #include<climits> 3 #include<queue> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 //int map[205][2]; 8 struct node 9 { 10 int x; 11 int y; 12 int step; 13 int kcount; 14 } map[205]; 15 int n, m, k, r; 16 int Sx, Sy; 17 int Tx, Ty; 18 int SPFA(int i); 19 bool legal(int Ax, int Ay, int Bx, int By); 20 int main() 21 { 22 scanf("%d %d %d %d", &n, &m, &k, &r); 23 for(int i = 0; i < n + m; i ++) 24 { 25 scanf("%d %d", &map[i].x, &map[i].y); 26 map[i].step = INT_MAX; 27 map[i].kcount = 0; 28 } 29 map[0].step = 0; 30 Sx = map[0].x; 31 Sy = map[0].y; 32 Tx = map[1].x; 33 Ty = map[1].y; 34 printf("%d", SPFA(0)); 35 } 36 bool legal(int Ax, int Ay, int Bx, int By) 37 { 38 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 39 return true; 40 else 41 return false; 42 } 43 int SPFA(int i) 44 { 45 queue<node> s; 46 node p; 47 // s.x = Sx; 48 // s.y = Sy; 49 // s.push(map[0]); 50 p.x = Sx; 51 p.y = Sy; 52 s.push(p); 53 while(!s.empty()) 54 { 55 p = s.front(); 56 s.pop(); 57 // if(p.x == Tx && p.y == Ty) 58 // return p.step; 59 60 for(int i = 0; i < n + m; i ++) 61 { 62 if(map[i].x == Tx && map[i].y == Ty) 63 return p.step; 64 if(i >= n && p.kcount == k) 65 continue; 66 if(legal(p.x, map[i].x, p.y, map[i].y)) 67 { 68 if(i >= n) 69 map[i].kcount = p.kcount ++; 70 s.push(map[i]); 71 if(map[i].step > p.step + 1){ 72 map[i].step = p.step + 1; 73 // printf("##\n"); 74 } 75 } 76 } 77 } 78 return 0; 79 } 80 //5 3 1 3 81 //0 0 82 //5 5 83 //0 3 84 //0 5 85 //3 5 86 //3 32 87 //4 4 88 //3 0
实在没招加了visit就40分,不加就30分。但感觉visit加的没有意义
1 #include<cstdio> 2 #include<climits> 3 #include<queue> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 //int map[205][2]; 8 struct node 9 { 10 int x; 11 int y; 12 int step; 13 int kcount; 14 } map[205]; 15 int n, m, k, r; 16 int Sx, Sy; 17 int Tx, Ty; 18 int visit[205]; 19 int SPFA(int i); 20 bool legal(int Ax, int Bx, int Ay, int By); 21 int main() 22 { 23 scanf("%d %d %d %d", &n, &m, &k, &r); 24 for(int i = 0; i < n + m; i ++) 25 { 26 scanf("%d %d", &map[i].x, &map[i].y); 27 map[i].step = INT_MAX; 28 map[i].kcount = 0; 29 } 30 map[0].step = 0; 31 Sx = map[0].x; 32 Sy = map[0].y; 33 Tx = map[1].x; 34 Ty = map[1].y; 35 printf("%d", SPFA(0)); 36 } 37 bool legal(int Ax, int Bx, int Ay, int By) 38 { 39 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 40 return true; 41 else 42 return false; 43 } 44 int SPFA(int i) 45 { 46 queue<node> s; 47 node p;// s.x = Sx;// s.y = Sy;// s.push(map[0]); 48 p.x = Sx; 49 p.y = Sy; 50 s.push(p); 51 visit[0] = 1; 52 while(!s.empty()) 53 { 54 p = s.front(); 55 s.pop(); 56 for(int i = 0; i < n + m; i ++) 57 { 58 if(visit[i]) 59 continue; 60 if(legal(p.x, map[i].x, p.y, map[i].y)) 61 { 62 if(p.x == map[i].x && p.y == map[i].y) 63 continue; 64 if(map[i].x == Tx && map[i].y == Ty) 65 return p.step; 66 if(i >= n) 67 { 68 if(p.kcount == k) 69 continue; 70 map[i].kcount = p.kcount ++; 71 } 72 if(map[i].step > p.step + 1) 73 { 74 map[i].step = p.step + 1;// printf("%d\n", map[i].step); 75 } 76 s.push(map[i]); 77 if(i < n) 78 visit[i] = 1; 79 } 80 } 81 } 82 return 0; 83 } 84 //5 3 1 3 85 //0 0 86 //5 5 87 //0 3 88 //0 5 89 //3 5 90 //3 3 91 //4 4 92 //3 0 93 94 //10 4 2 1 95 //0 0 96 //5 0 97 //0 1 98 //0 2 99 //0 3 100 //1 3 101 //3 0 102 //3 1 103 //3 2 104 //3 3 105 //1 0 106 //2 0 107 //2 3 108 //4 0
调试发现step那里不行,依旧64行的问题
1 #include<cstdio> 2 #include<climits> 3 #include<queue> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 //int map[205][2]; 8 struct node 9 { 10 int x; 11 int y; 12 int step; 13 int kcount; 14 } map[205]; 15 int n, m, k, r; 16 int Sx, Sy; 17 int Tx, Ty; 18 int SPFA(int i); 19 bool legal(int Ax, int Bx, int Ay, int By); 20 int main() 21 { 22 scanf("%d %d %d %d", &n, &m, &k, &r); 23 for(int i = 0; i < n + m; i ++) 24 { 25 scanf("%d %d", &map[i].x, &map[i].y); 26 map[i].step = INT_MAX; 27 map[i].kcount = 0; 28 } 29 map[0].step = 0; 30 Sx = map[0].x; 31 Sy = map[0].y; 32 Tx = map[1].x; 33 Ty = map[1].y; 34 printf("%d", SPFA(0)); 35 } 36 bool legal(int Ax, int Bx, int Ay, int By) 37 { 38 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 39 return true; 40 else 41 return false; 42 } 43 int SPFA(int i) 44 { 45 queue<node> s; 46 node p;// s.x = Sx;// s.y = Sy;// s.push(map[0]); 47 p.x = Sx; 48 p.y = Sy; 49 s.push(p); 50 while(!s.empty()) 51 { 52 p = s.front(); 53 s.pop(); 54 for(int i = 1; i < n + m; i ++) 55 { 56 if(legal(p.x, map[i].x, p.y, map[i].y)) 57 { 58 if(p.x == map[i].x && p.y == map[i].y) 59 continue; 60 if(map[i].x == Tx && map[i].y == Ty) 61 return p.step; 62 map[i].kcount = p.kcount; 63 if(i >= n) 64 { 65 if(p.kcount == k)//问题1,还有就是每一个的线路要赋值p.kcount 66 continue; 67 map[i].kcount = p.kcount + 1; 68 printf("$%d\n", p.kcount); 69 // if(p.x == 2 && p.y == 0) 70 // printf("^%d\n", map[i].kcount); 71 // if(p.x == 1 && p.y == 0) 72 // printf("^%d\n", map[i].kcount); 73 // if(i == 10) 74 // printf("^%d\n", map[i].kcount); 75 printf("^%d\n", map[12].kcount);//没进去 76 } 77 if(map[i].step > p.step + 1)//这样写进行不下去,visit又死锁 78 { 79 map[i].step = p.step + 1;// printf("%d\n", map[i].step); 80 } 81 s.push(map[i]); 82 } 83 } 84 } 85 return 0; 86 } 87 //5 3 1 3 88 //0 0 89 //5 5 90 //0 3 91 //0 5 92 //3 5 93 //3 3 94 //4 4 95 //3 0 96 97 //10 4 2 1 98 //0 0 99 //5 0 100 //0 1 101 //0 2 102 //0 3 103 //1 3 104 //3 0 105 //3 1 106 //3 2 107 //3 3 108 //1 0 109 //2 0 110 //2 3 111 //4 0
这里的这句话 if(map[i].step > p.step + 1)
盗用了最短的那个step,所以
10 4 2 1
0 0
5 0
0 1
0 2
0 3
1 3
3 0
3 1
3 2
3 3
1 0
2 0
2 3
4 0
会输出4
1 #include<cstdio> 2 #include<climits> 3 #include<queue> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 //int map[205][2]; 8 struct node 9 { 10 int x; 11 int y; 12 int step; 13 int kcount; 14 } map[205]; 15 int n, m, k, r; 16 int Sx, Sy; 17 int Tx, Ty; 18 int SPFA(int i); 19 bool legal(int Ax, int Bx, int Ay, int By); 20 int main() 21 { 22 scanf("%d %d %d %d", &n, &m, &k, &r); 23 for(int i = 0; i < n + m; i ++) 24 { 25 scanf("%d %d", &map[i].x, &map[i].y); 26 map[i].step = INT_MAX; 27 map[i].kcount = 0; 28 } 29 map[0].step = 0; 30 Sx = map[0].x; 31 Sy = map[0].y; 32 Tx = map[1].x; 33 Ty = map[1].y; 34 printf("%d", SPFA(0)); 35 } 36 bool legal(int Ax, int Bx, int Ay, int By) 37 { 38 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 39 return true; 40 else 41 return false; 42 } 43 int SPFA(int i) 44 { 45 queue<node> s; 46 node p;// s.x = Sx;// s.y = Sy;// s.push(map[0]); 47 p.x = Sx; 48 p.y = Sy; 49 s.push(p); 50 while(!s.empty()) 51 { 52 p = s.front(); 53 s.pop(); 54 for(int i = 1; i < n + m; i ++) 55 { 56 if(legal(p.x, map[i].x, p.y, map[i].y)) 57 { 58 if(p.x == map[i].x && p.y == map[i].y) 59 continue; 60 if(map[i].x == Tx && map[i].y == Ty) 61 return p.step; 62 map[i].kcount = p.kcount; 63 if(map[i].x == 4 && map[i].y == 0) 64 printf("_%d %d_\n", map[i].kcount, map[i].step);//输出2,对的,但是后面变1了 65 // printf("_%d %d_\n", map[2].kcount, map[2].step); 66 if(i >= n) 67 { 68 if(p.kcount == k)//问题1,还有就是每一个的线路要赋值p.kcount 69 continue; 70 map[i].kcount = p.kcount + 1; 71 } 72 if(map[i].step > p.step + 1)//这样写进行不下去,visit又死锁 73 map[i].step = p.step + 1;// printf("%d\n", map[i].step); 74 s.push(map[i]); 75 } 76 } 77 } 78 return 0; 79 } 80 //5 3 1 3 81 //0 0 82 //5 5 83 //0 3 84 //0 5 85 //3 5 86 //3 3 87 //4 4 88 //3 0 89 90 //10 4 2 1 91 //0 0 92 //5 0 93 //0 1 94 //0 2 95 //0 3 96 //1 3 97 //3 0 98 //3 1 99 //3 2 100 //3 3 101 //1 0 102 //2 0 103 //2 3 104 //4 0
现在感觉step判断多余,去了还是不行,超时,还是40却提示了个运行超时,之前没提示,只是1.6s。。
我认为step判断多余,我想的是
如果已经走过去了,那后面再来的点更改距离就无所谓了,
而前面已经走过的点如果记录的最短距离,我现在这个step大于那个也没事,因为如果你真小且新增设的点没有超过k的话,会早就到达终点输出最后最小值的。
但其实不然,真正的SPFA,就拿最后一个点来说,前面经过条条大路过来,我剩下三条路径,最后的那条路径是比较长的,所以不能不比较。
1 #include<cstdio> 2 #include<climits> 3 #include<queue> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 //int map[205][2]; 8 struct node 9 { 10 int x; 11 int y; 12 int step; 13 int kcount; 14 } map[205]; 15 int n, m, k, r; 16 int Sx, Sy; 17 int Tx, Ty; 18 int SPFA(int i); 19 bool legal(int Ax, int Bx, int Ay, int By); 20 int main() 21 { 22 scanf("%d %d %d %d", &n, &m, &k, &r); 23 for(int i = 0; i < n + m; i ++) 24 { 25 scanf("%d %d", &map[i].x, &map[i].y); 26 map[i].step = INT_MAX; 27 map[i].kcount = 0; 28 } 29 map[0].step = 0; 30 Sx = map[0].x; 31 Sy = map[0].y; 32 Tx = map[1].x; 33 Ty = map[1].y; 34 printf("%d", SPFA(0)); 35 } 36 bool legal(int Ax, int Bx, int Ay, int By) 37 { 38 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 39 return true; 40 else 41 return false; 42 } 43 int SPFA(int i) 44 { 45 queue<node> s; 46 node p;// s.x = Sx;// s.y = Sy;// s.push(map[0]); 47 p.x = Sx; 48 p.y = Sy; 49 s.push(p); 50 while(!s.empty()) 51 { 52 p = s.front(); 53 s.pop(); 54 for(int i = 1; i < n + m; i ++) 55 { 56 if(legal(p.x, map[i].x, p.y, map[i].y)) 57 { 58 if(p.x == map[i].x && p.y == map[i].y) 59 continue; 60 if(map[i].x == Tx && map[i].y == Ty) 61 return p.step; 62 map[i].kcount = p.kcount; 63 // if(map[i].x == 4 && map[i].y == 0) 64 // printf("_%d %d_\n", map[i].kcount, map[i].step);//输出2,对的,但是后面变1了 65 // printf("_%d %d_\n", map[2].kcount, map[2].step); 66 if(i >= n) 67 { 68 if(p.kcount == k)//问题1,还有就是每一个的线路要赋值p.kcount 69 continue; 70 map[i].kcount = p.kcount + 1; 71 } 72 // if(map[i].step > p.step + 1)//这样写进行不下去,visit又死锁 73 map[i].step = p.step + 1;// printf("%d\n", map[i].step); 74 s.push(map[i]); 75 } 76 } 77 } 78 return 0; 79 } 80 //5 3 1 3 81 //0 0 82 //5 5 83 //0 3 84 //0 5 85 //3 5 86 //3 3 87 //4 4 88 //3 0 89 90 //10 4 2 1 91 //0 0 92 //5 0 93 //0 1 94 //0 2 95 //0 3 96 //1 3 97 //3 0 98 //3 1 99 //3 2 100 //3 3 101 //1 0 102 //2 0 103 //2 3 104 //4 0
纠结:为什么acm大佬说代码思路错了重写比较好,原有思路上改进不是更厉害么
太糟糕了,那个step有问题,是上一个,所以打算重写
中途还越界了,因为我是想跳过起始点不用再压入队列,所以就for没从0开始,后面dec_都是INT_MAX所以+1就崩了。(哎。。比较混乱,我也不知道当时为什么这么写的了。就是82行那个。。。。)
这里的dec_,我试了一下dec作为数组是没有问题的,但是这里的AC代码,将dec_改为dec是会报错的。很奇怪。
C:\Users\GerJCS岛\Desktop\CCF.cpp|28|error: reference to 'dec' is ambiguous
【原因和解决方法】
一般是由于定义的xx变量名称与库函数中的函数名xx有重名现象,通常做法是将定义的变量的首字母大写就不会重名了。
int函数最后要return 0;不然会报错
warning: control reaches end of non-void function [-Wreturn-type
之前错误思路用到了 点 是否在矩形内部
方法一:大的x赋给max_x,小的......,最后判断在范围之内即可。
方法二:没看懂
本题的两点距离不超过r
距离公式,直接平方;
坐标轴的两点就是,差的绝对值
还有一个什么判断点是否在圆内?不管了,这里用不到,先不考虑
1 #include<cstdio> 2 #include<climits> 3 #include<cstring> 4 #include<queue> 5 #include <iostream> 6 #include <algorithm> 7 using namespace std; 8 //int map[205][2]; 9 struct node 10 { 11 int x; 12 int y; 13 // int step; 14 int kcount;//其实应该重写的,这里我没有续写是感觉浪费时间没必要,且这里的kcount应该是变量的不应该是成员变量。 15 } map[205]; 16 int n, m, k, r; 17 int Sx, Sy; 18 int Tx, Ty; 19 int SPFA(int i); 20 bool legal(int Ax, int Bx, int Ay, int By); 21 int dec_[205][105];//居然C:\Users\GerJCS岛\Desktop\CCF.cpp|27|error: reference to 'dec' is ambiguous| 22 int main() 23 { 24 scanf("%d %d %d %d", &n, &m, &k, &r); 25 for(int i = 0; i < n + m; i ++) 26 { 27 scanf("%d %d", &map[i].x, &map[i].y); 28 // map[i].step = INT_MAX; 29 map[i].kcount = 0; 30 } 31 // for(int i = 0; i < n + m; i ++) 32 // for(int j = 0; j < m; j ++) 33 for(int i = 0; i < 201; i ++) 34 for(int j = 0; j < 101; j ++) 35 dec_[i][j] = INT_MAX; 36 dec_[0][0] = 0; 37 38 // map[0].step = 0; 39 Sx = map[0].x; 40 Sy = map[0].y; 41 Tx = map[1].x; 42 Ty = map[1].y; 43 printf("%d\n", SPFA(0)); 44 printf("%d %d\n", dec_[6][2], dec_[6][1]); 45 } 46 bool legal(int Ax, int Bx, int Ay, int By) 47 { 48 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 49 return true; 50 else 51 return false; 52 } 53 int SPFA(int i) 54 { 55 queue<node> s; 56 node p;// s.x = Sx;// s.y = Sy;// s.push(map[0]); 57 p.x = Sx; 58 p.y = Sy; 59 s.push(p); 60 while(!s.empty()) 61 { 62 p = s.front(); 63 s.pop(); 64 for(int i = 0; i < n + m; i ++) 65 { 66 if(legal(p.x, map[i].x, p.y, map[i].y)) 67 { 68 if(p.x == map[i].x && p.y == map[i].y) 69 continue; 70 if(map[i].x == Tx && map[i].y == Ty) 71 return dec_[1][p.kcount]; 72 map[i].kcount = p.kcount; 73 // if(map[i].x == 4 && map[i].y == 0) 74 // printf("_%d %d_\n", map[i].kcount, map[i].step);//输出2,对的,但是后面变1了 75 // printf("_%d %d_\n", map[2].kcount, map[2].step); 76 if(i >= n) 77 { 78 if(p.kcount == k)//问题1,还有就是每一个的线路要赋值p.kcount 79 continue; 80 map[i].kcount = p.kcount + 1; 81 } 82 if(dec_[i][map[i].kcount] > dec_[i][p.kcount] + 1){//这样写进行不下去,visit又死锁 83 printf("TEST %d\n", dec_[0][0]); 84 printf("$$%d %d$\n", dec_[i][map[i].kcount], dec_[i][p.kcount] );//卧槽,越界了 85 dec_[i][map[i].kcount] = dec_[i][p.kcount] + 1;//这样写进行不下去,visit又死锁 86 // map[i].step = p.step + 1;// printf("%d\n", map[i].step); 87 s.push(map[i]); 88 } 89 } 90 } 91 } 92 return 0; 93 } 94 ////5 3 1 3 95 ////0 0 96 ////5 5 97 ////0 3 98 ////0 5 99 ////3 5 100 ////3 3 101 ////4 4 102 ////3 0 103 // 104 ////10 4 2 1 105 ////0 0 106 ////5 0 107 ////0 1 108 ////0 2 109 ////0 3 110 ////1 3 111 ////3 0 112 ////3 1 113 ////3 2 114 ////3 3 115 ////1 0 116 ////2 0 117 ////2 3 118 ////4 0 119 120 // 121 //#include <iostream> 122 //#include <algorithm> 123 //#include <queue> 124 //#define INF 0x7f7f7f7f 125 // 126 //using namespace std; 127 // 128 //struct point 129 //{ 130 // long long x; 131 // long long y; 132 //} p[201]; 133 //struct node 134 //{ 135 // int i; //表示到达的路由器 i 136 // int k; //表示 k 个增设路由器 137 //}; 138 //int d[201][201]; //用d[i][k]表示从起点到达i的最短路径,经过了k个增设路由器 139 //bool vis[201][201];//入队标志 ,用vis[i][k] i表示节点,k表示新增节点个数 140 //bool map[201][201]; //图矩阵 141 // 142 ////spfa 算法 143 //int spfa(int n, int m, int k) 144 //{ 145 // queue<node> q; 146 // for(int i = 0; i < 201; i++) //初始化 vis,d 147 // { 148 // for(int j = 0; j < 201; j++) 149 // { 150 // vis[i][j] = 0;//未入队 151 // d[i][j] = INF;//路径无穷大 152 // } 153 // } 154 // node front, tem; 155 // front.i = 0;//源点是 0 156 // front.k = 0;//增点也是 0个 157 // d[front.i][front.k] = 0; // 158 // q.push(front); 159 // while(!q.empty()) 160 // { 161 // front = q.front(); 162 // q.pop(); 163 // vis[front.i][front.k] = 0;//出队 164 // for(int i = 0; i < n + m; i++) 165 // { 166 // if(map[front.i][i]) //如果从front.x 到 i 有路径 167 // { 168 // tem.i = i; 169 // tem.k = front.k; 170 // if(i >= n) 171 // tem.k++; 172 // if(tem.k <= k && d[tem.i][tem.k] > d[front.i][front.k] + 1)//我觉得这里不用判断大小吧?????对于后可以,对于本局也可以???????????????????????? 173 // { 174 // if(tem.i == 6) 175 // printf("-%d %d-\n", d[tem.i][tem.k], d[front.i][front.k]); 176 // 177 // d[tem.i][tem.k] = d[front.i][front.k] + 1; 178 // 179 // if(tem.i == 6) 180 // printf("……%d %d\n", d[tem.i][tem.k], d[front.i][front.k]); 181 // 182 // if(vis[tem.i][tem.k] == 0) 183 // { 184 // q.push(tem); 185 // vis[tem.i][tem.k] = 1; 186 // } 187 // } 188 // } 189 // } 190 // } 191 // int ans = INF; 192 // for(int i = 0; i <= k; i++) 193 // { 194 // ans = min(ans, d[1][i]); 195 // //cout<<d[1][i]<<" "; 196 // } 197 // return ans; 198 //} 199 // 200 // 201 // 202 //int main() 203 //{ 204 //// printf("%d", INF); 205 //// 2139062143 206 // int n, m, k; 207 // long long r; 208 // cin >> n >> m >> k >> r; 209 // for(int i = 0; i < n + m; i++) 210 // { 211 // cin >> p[i].x >> p[i].y; 212 // } 213 // for(int i = 0; i < n + m; i++) //构建图 214 // { 215 // for(int j = i + 1; j < n + m; j++) 216 // { 217 // if((p[i].x - p[j].x) * (p[i].x - p[j].x) + (p[i].y - p[j].y) * (p[i].y - p[j].y) <= r * r) 218 // { 219 // map[i][j] = 1; 220 // map[j][i] = 1; 221 // } 222 // } 223 // } 224 // int ans = spfa(n, m, k); 225 // cout << ans - 1; 226 // return 0; 227 //}
我做后参考了 题解 才懂的,写的非常好。我是最开始查很多题解都是要设置二维数组,但是死活不理解什么意思,通过自己写了好几次错误代码找出问题所在,才明白为什么要用二维数组存储一个 k 一个 i ,最后翻到这个题解再结合上面链接里的SPFA讲解才懂,最后AC。
最后A掉了
我改了两次,重点80行:
if(dec_[i][mid_k] > dec_[willpush.i][willpush.k] + 1)
i 对应willpush.i
mid_k对应willpush.k
即 都是这一次的 与 都是轴点的 作比较。有点像hdoj的走楼梯,好像也有点像动态规划的表达式,还像那个递推公式。
这是这道题的巧妙所在,也是精髓,SPFA的精髓。
if(dec_[i][mid_k] > dec_[willpush.i][willpush.k] + 1)
1 //再一次提交 2 //https://paste.ubuntu.com/p/XjYJ6dVXBV/ 3 //80分 4 5 //小问题,大错误.d对队列和BFS/SPFA思路不清晰 6 //https://paste.ubuntu.com/p/bsRzbhq5Z4/ 7 8 9 #include<cstdio> 10 #include<climits> 11 #include<cstring> 12 #include<queue> 13 #include <iostream> 14 #include <algorithm> 15 using namespace std; 16 struct node 17 { 18 int x; 19 int y; 20 int i; 21 int k; 22 }map[205]; 23 int n, m, k; 24 long long int r; 25 int Sx, Sy; 26 int Tx, Ty; 27 int SPFA(int i); 28 bool legal(long long int Ax, long long int Bx, long long int Ay, long long int By); 29 int dec_[205][105]; 30 int main() 31 { 32 scanf("%d %d %d %lld", &n, &m, &k, &r); 33 for(int i = 0; i < n + m; i ++) 34 scanf("%d %d", &map[i].x, &map[i].y); 35 for(int i = 0; i < 201; i ++) 36 for(int j = 0; j < 101; j ++) 37 dec_[i][j] = INT_MAX - 10; 38 dec_[0][0] = 0; 39 Sx = map[0].x; 40 Sy = map[0].y; 41 Tx = map[1].x; 42 Ty = map[1].y; 43 printf("%d\n", SPFA(0)); 44 } 45 bool legal(long long int Ax, long long int Bx, long long int Ay, long long int By) 46 { 47 if((Ax - Bx) * (Ax - Bx) + (Ay - By) * (Ay - By) <= r * r) 48 return true; 49 else 50 return false; 51 } 52 int SPFA(int i) 53 { 54 queue<node> s; 55 node mid;//中转 56 node willpush;//即将压入 57 node next; 58 mid.x = Sx; 59 mid.y = Sy; 60 mid.i = 0; 61 mid.k = 0; 62 s.push(mid); 63 int mid_k; 64 while(!s.empty()){ 65 willpush = s.front(); 66 s.pop(); 67 for(int i = 0; i < n + m; i ++){ 68 if(legal(willpush.x, map[i].x, willpush.y, map[i].y)) 69 { 70 if(willpush.x == map[i].x && willpush.y == map[i].y) 71 continue; 72 if(map[i].x == Tx && map[i].y == Ty) 73 return dec_[willpush.i][willpush.k];//这些个坐标,变量很有讲究 74 mid_k = willpush.k; 75 if(i >= n){ 76 if(willpush.k == k) 77 continue; 78 mid_k = willpush.k + 1; 79 } 80 if(dec_[i][mid_k] > dec_[willpush.i][willpush.k] + 1){ 81 dec_[i][mid_k] = dec_[willpush.i][willpush.k] + 1; 82 next.x = map[i].x; 83 next.y = map[i].y;//调试好久。。。。 84 next.i = i; 85 next.k = mid_k; 86 s.push(next); 87 } 88 } 89 } 90 } 91 return 0; 92 } 93 94 //5 3 1 3 95 //0 0 96 //5 5 97 //0 3 98 //0 5 99 //3 5 100 //3 3 101 //4 4 102 //3 0 103 104 //10 4 2 1 105 //0 0 106 //5 0 107 //0 1 108 //0 2 109 //0 3 110 //1 3 111 //3 0 112 //3 1 113 //3 2 114 //3 3 115 //1 0 116 //2 0 117 //2 3 118 //4 0 119 120 121 //最后满分
PS:所有的BFS接法都有点不可通过。所有的visit都可以去掉
我真的很疑惑为什么这么多人(看着应该是个大佬啊),却都用BFS来做。。。。可能刚刷不太了解细节,再刷刷感悟一下再回头来看这个题目吧
更多题解(我参考了很多题解才看明白的,因为可能有些描述不是很能立刻理解)
https://blog.csdn.net/qq_32445015/article/details/79796830
好烦,我不习惯看别人代码,这个代码纯bfs,为什么能满分。(而且还有人看懂了,做出了评论指正,哎)
又是在拖延,难道工作都是要这么看代码的吗?那些只会C语言跨考HIT,科软的朋友两年能看会代码了么
强迫症思维快疯了。。。大佬们都是迅速写,迅速交流(或者网上迅速看懂题解),如果BFS错误思路AC了再看更多题解就能立马反应过来错在哪里。而我掰不开镊子一样,嬷嬷丢,来回转圈圈,就算正解SPFA AC了,最后看BFS还是看不懂。也不愿意回顾,强迫写题解。。。可能这就是为什么考2次都。。。。。。逃避和不想复习吧。。。很痛苦。。。这个时候了还魔怔一样刷CCF,哪怕刷,别人也是PAT,哎。。。。
哎,像一个死废物一样,陷入一个怪圈循环。。。黑暗之海。。。我这么弱还活在世界上,真的对不起。。想要做出改变。。。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号