梯度、散度、旋度

• 前言

  感谢视频作者，无意间刷到，把旋度和散度讲的很通俗易懂，可视化也很直观。本文为学习笔记。

  https://player.bilibili.com/player.html?aid=468216938&bvid=BV1a541127cX&cid=574493213&page=1&high_quality=1

结论：#

• 理解1：
  

  • 散度是通量的体密度，即通量的微分；
  • 旋度是环量的面密度，即环量的微分；
    
    

• 理解2:

  区别在于如何与$\nabla$进行运算：
  

  数学概念	特点	符号	Numpy函数
  梯度	数量积、哈达玛积	$\odot$	np.multiply 或者 *
  散度	点乘、内积	$\cdot$	np.dot
  旋度	叉乘、外积	$\times$或者 $\otimes$	np.cross

---

1. 梯度（graident）#

对于标量场和矢量场

---

1.1 对于标量场#

nabla算子把数量场变成了向量场，即 $\mathbb{R} \rightarrow \mathbb{R}^n$：

$$\nabla = \begin{bmatrix}\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}\frac{\partial}{\partial x_3}, \dots, \frac{\partial}{\partial x_n}\end{bmatrix}^T$$

$\nabla$和函数的数量乘$\nabla f$ 称为函数梯度

$$\nabla_{\boldsymbol{x}} f(\boldsymbol{x})\overset{\underset{\mathrm{def}}{}}{=}\begin{bmatrix} \frac{\partial }{\partial x_1}\\ \frac{\partial }{\partial x_2}\\ \vdots \\ \frac{\partial }{\partial x_n} \end{bmatrix} \odot f= \left[ \frac{\partial f(\boldsymbol{x})}{\partial x_1}, \frac{\partial f(\boldsymbol{x})}{\partial x_2},\cdots,\frac{\partial f(\boldsymbol{x})}{\partial x_n} \right]^T=\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}$$

1.2 对矢量场#

$m$维向量函数$\boldsymbol{f}(\boldsymbol{x})=[f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_m(\boldsymbol{x})]$相对于$n$维实向量$x$的梯度为$n×m$矩阵，$\mathbb{R}^{m} \rightarrow \mathbb{R}^{n \times m}$ ：

$$\nabla\overset{\underset{\mathrm{def}}{}}{=}\begin{bmatrix}\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}\frac{\partial}{\partial x_3}, \dots, \frac{\partial}{\partial x_n}\end{bmatrix}^T$$

$$\begin{aligned}\nabla_{\boldsymbol{x}} \boldsymbol{f}(\boldsymbol{x}) &=\frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial \boldsymbol{x}} \\ & = \begin{bmatrix}\frac{\partial}{\partial x_1}\\ \frac{\partial}{\partial x_2}\\\frac{\partial}{\partial x_3}\\\vdots\\\frac{\partial}{\partial x_n}\end{bmatrix} \odot\boldsymbol [f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_m(\boldsymbol{x})] \\ &= \begin{bmatrix} \frac{\partial f_1(\boldsymbol{x})}{\partial x_1} &\frac{\partial f_2(\boldsymbol{x})}{\partial x_1} & \cdots & \frac{\partial f_m(\boldsymbol{x})}{\partial x_1} \\ \frac{\partial f_1(\boldsymbol{x})}{\partial x_2} &\frac{\partial f_2(\boldsymbol{x})}{\partial x_2} & \cdots & \frac{\partial f_m(\boldsymbol{x})}{\partial x_2} \\ \vdots &\vdots & \ddots & \vdots \\ \frac{\partial f_1(\boldsymbol{x})}{\partial x_n} &\frac{\partial f_2(\boldsymbol{x})}{\partial x_n} & \cdots &\frac{\partial f_m(\boldsymbol{x})}{\partial x_n} \\ \end{bmatrix} \\ \end{aligned}$$

1.3 梯度的性质：#

• 
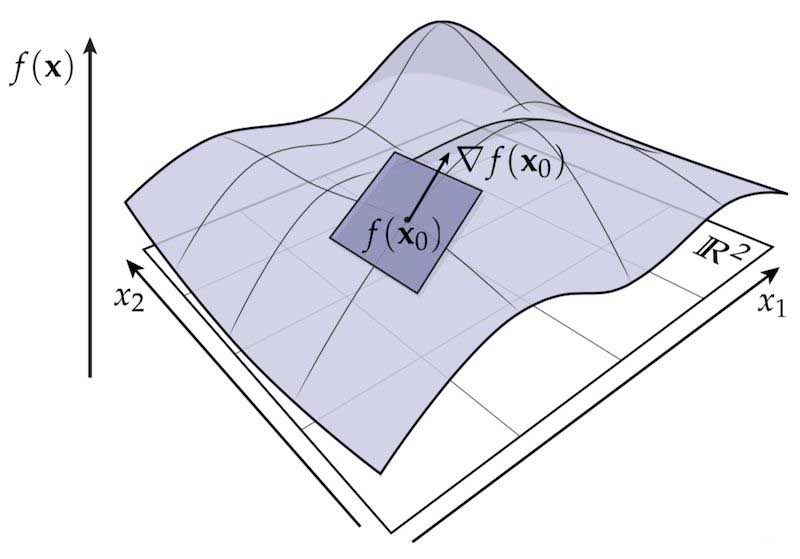
  • 沿着梯度方向走，函数值增大
  • 沿着相反于梯度的方向走，函数值减小
  • 垂直于梯度方向，函数值不变

--image

2. 散度（divergence）#

---

对于向量场

---

2.1 定义#

$\nabla$和函数的点乘$\nabla f$ 称为函数散度，某点散度代表了该点向外的通量体密度. $\mathbb{R}^n \rightarrow \mathbb{R}$。

设某个三维矢量场为$f,$ 那么散度

$$\begin{aligned}\mathbf{div} (\mathbb{f}) &= \nabla \cdot f \\&=\begin{bmatrix} {\frac{\partial f_x}{\partial x} , \frac{\partial f_y}{\partial y}, \frac{\partial f_z}{\partial z} }\end{bmatrix}\begin{bmatrix} f_x \\ f_y \\f_x\end{bmatrix}\\&=\frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}\end{aligned}$$

这里的$[f_x, f_Y,f_z] = {f} \cdot \vec{n}$

2.2 高斯公式#

👉 **定理： ** 设空间有限比克区域为$\Omega$，$\partial \Omega$ 为该区域的封闭外曲面，那么**高斯公式**：

$$\underbrace{\iiint\limits_\Omega \overbrace{\nabla \cdot {f}}^{散度} dV}_{内部所有散度的贡献} = \underbrace{\oiint\limits_{\partial \Omega}{f} \cdot \vec{n} dS }_{流过边界的通量}$$

对于三维矢量，高斯公式可以表示为：

$$\iiint \limits_\Omega (\frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}) dV = \oiint \limits_{\partial \Omega}f_zdydz+f_ydxdz+f_zdxdy$$

--image

• 物理意义：

  某点散度代表了该点向外的通量体密度，其物理意义可以理解为：定量给出向量场中任一点是否为源点或汇点。若某点散度等于0，则说明其通量为0，流进=流出；若某点散度大于0，说明流出>流进，相当于一个源点(source)；若某点散度小于0，说明流出<流进，相当于一个汇点(sink)。

应用：

流体力学中不可压缩条件为：速度场的散度为0。

→ 推导:

不可压缩意味着密度为常数，根据欧拉描述下（基于场的描述）质量连续性方程：

$\frac{d \rho}{d t}+\rho \nabla \cdot v=0$，由于密度为常数，因此其对时间的全导数应为0，即$\frac{d \rho}{d t}=0$，因此速度散度$\nabla \cdot v$为0。

3. 旋度（curl）#

3.1 定义#

$\nabla$和函数的叉乘$\nabla \times f$ 称为函数旋度，某点散度代表了该点局部旋涡强度(我把散度想象成动量密度，旋度想象成旋转动量密度) . $\mathbb{R}^n \rightarrow \mathbb{R}^n$（受限于叉乘，通常$n\leqslant 3$）。

$$\begin{aligned} \mathbf{curl}(f)&= \nabla \times \textbf{f}\\ &= \begin{bmatrix} {\frac{\partial f_x}{\partial x} , \frac{\partial f_y}{\partial y}, \frac{\partial f_z}{\partial z} }\end{bmatrix} \times \begin{bmatrix} f_x \\ f_y \\f_x\end{bmatrix} \\&= \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u & v & w\end{bmatrix} \\& = \begin{bmatrix} \frac{\partial f_z}{\partial y} - \frac{\partial f_y}{\partial z} \\ \frac{\partial f_x}{\partial z} - \frac{\partial f_z}{\partial x} \\\frac{\partial f_y}{\partial x} - \frac{\partial f_x}{\partial y} \\\end{bmatrix} \end{aligned}$$

3.2 斯托克斯公式#

👉 **定理**： 对于分片光滑的封闭曲面$S$，闭合曲线 $\partial S$是分片光滑曲面 的边界。那么**斯托克斯公式**：

$$\underbrace{\iint\limits_\Omega \overbrace{\nabla \times {f}}^{旋度} dS}_{曲面上旋度的贡献} = \underbrace{\oint\limits_{\partial }{f} \cdot \vec{n} dl }_{围绕边界的环量}$$

即旋度的区域$**S$面积分等于向量场围绕物体边界** $\partial S$的线积分。即旋度的区域$**S$面积分等于向量场围绕物体边界** $\partial S$的线积分。

应用：

流体力学中：在连续介质中,速度的旋度等于角速度的两倍.

即：$**curl(\vec v)=\nabla \times \vec{v}=2(\vec w)**$

→ 推导: ( 没看懂😂 )

$$\begin{aligned} \nabla \times \mathbf{v}&=\nabla \times (\boldsymbol{w} \times \mathbf{r} ) \\ &=(\frac{\partial}{\partial x_i}\vec e_i) \times (w_j\vec e_j \times r_k \vec e_k) \\ &=(\frac{\partial}{\partial x_i}\vec e_i) \times (\varepsilon_{jkn}w_j r_k \vec e_n ) \\&=\frac{\partial}{\partial x_i} (w_jr_k) \varepsilon_{jkn}\varepsilon_{inm}\vec e_m \\ &=w_j\delta_{ki}\varepsilon_{jkn}\varepsilon_{inm}\vec e_m \\ &=w_j\varepsilon_{jkn}\varepsilon_{knm}\vec e_m \\ &=w_j2\delta_{jm}\vec e_m \\&=2w_j\vec e_j \end{aligned}$$

4. $\nabla$ 、$\Delta$算子#

$$\nabla = \begin{bmatrix}\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2},\frac{\partial}{\partial x_3}, \dots, \frac{\partial}{\partial x_n}\end{bmatrix}^T$$

• $\nabla$和$\nabla$做内积：

  求得是 梯度的散度，即 $\nabla \cdot \nabla$， 为了不混淆，将它记为拉普拉斯算子，$\Delta = \nabla^2 = \nabla \cdot \nabla^T$：

$$\begin{aligned} \Delta &= \nabla^2\\ &= \nabla \cdot \nabla^T \\&= \begin{bmatrix}\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2},\frac{\partial}{\partial x_3}, \dots, \frac{\partial}{\partial x_n}\end{bmatrix} \begin{bmatrix}\frac{\partial}{\partial x_1}\\ \frac{\partial}{\partial x_2}\\ \frac{\partial}{\partial x_3}\\ \vdots\\ \frac{\partial}{\partial x_n}\end{bmatrix} \\&= \frac{\partial^2} {\partial x_1^2} + \frac{\partial^2} {\partial x_2^2}+ \dots + \frac{\partial^2} {\partial x_n^2}\end{aligned}$$

• $\nabla$和$\nabla^T$数量积:

  求得是多元函数的二阶导，即海塞矩阵$H=\nabla \nabla^T$：

$$\begin{aligned}H &= \nabla \odot \nabla^T\\ &= \begin{bmatrix}\frac{\partial}{\partial x_1}\\ \frac{\partial}{\partial x_2}\\ \frac{\partial}{\partial x_3}\\ \vdots\\ \frac{\partial}{\partial x_n}\end{bmatrix} \odot \begin{bmatrix}\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2},\frac{\partial}{\partial x_3}, \dots, \frac{\partial}{\partial x_n}\end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial^2} {\partial x_1^2} & \cdots &\frac{\partial^2} {{\partial x_1} {\partial x_n}} \\ {\vdots}&{\ddots} & {\vdots}\\ \frac{\partial^2} {{\partial x_1} {\partial x_n}} & \cdots & \frac{\partial^2} {\partial x_n^2} \end{bmatrix} \end{aligned}$$

---

参考：#

1. 梯度、散度、旋度与矢量分析 - Hsuty的文章 - 知乎
2. 【nabla算子】与梯度、散度、旋度