1 批量状态估计和最大后验估计
1.1 复习运动方程和观测方程
\[\left\{
\begin{array}{c}
x_k=f(x_{k-1},u_k)+ w_k \\
z_{k,j}=h(y_i, x_k)+v_{k,j}
\end{array}
\right. \Rightarrow
\]
1.2 估计的本质:
对机器人的估计,本质上就是已知输入数据 \(u_k\)和观测数据 \(z _{k,j}\)的条件下,求机器人位姿 \(x_k\) 和路标点 \(y _i\)的条件概率分布\(P(x,y∣z,u)\)
\[\begin{align}\overbrace{P(x,y|z,u)}^{后验概率}&= \frac{P(z,u|x,y)P(x,y)}{P(z,u)}\\ &\approx \underbrace{P(z,u|x,y)}_{似然} \ \underbrace{P(x,y)}_{先验概率}\end{align}
\]
- 若不知道控制输入\(u\),只有所有观测图像\(z\),那么这个问题变为估计\({P(x,y|z)}\),称为SfM(Structure from Motion),目的是从观测图像估计相机参数及三维点位置
- 直接求后验分布(由果索因)是困难的,可以求一个最优估计,使得在该\((x,y)\)下后验概率最大化(即最有可能发生现在的结果\((z,u)\))。最大后验概率相当于最大化似然和先验的乘积:
\[\begin{align}
\overbrace{(x,y)^*_{MAP}}^{最大后验估计}
&=argmax{P(x,y∣z,u)} \\
&=argmax{\frac{P(z,u|x,y)P(x,y)}{\underbrace{P(z,u)}_{此项与x,y无关,可以去掉}}} \\
&=argmax{{P(z,u|x,y)P(x,y)}}
\end{align}
\]
- 假如不知道机器人的位姿或者路标位置,即不知道先验,则可以求最大似然估计:
\[{(x,y)^*_{MLE}}
=argmax{P(z,u∣x,y)}
\]
2 最小二乘法
-
什么是最小二乘
任意维度高斯分布\(x\sim \mathcal{N}(\mu,\Sigma)\),概率密度函数为:
\[P(x)=\frac{1}{\sqrt{(2\pi)^Ndet(\Sigma)}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) \\
\Downarrow\Downarrow\Downarrow 负对数\\
-ln(P(x)) = \frac{1}{2}ln((2\pi)^Ndet(\Sigma))+\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) \\
\Downarrow\Downarrow\Downarrow \\
(x)^*_{MLE}=argmax(P(x))=argmin((x-\mu)^T\Sigma^{-1}(x-\mu))
\]
2.1 基于观测数据\(z\)的最小二乘(单次数据)
对于一次观测\(z_{k,j}\) (时刻k,观测点j),观测方程为\(z_{k,j}=h(y_i, x_k)+v_{k,j}\),假设噪声服从高斯分布 \(v_{k,j}\sim\mathcal{N}({0, Q_{k,j}})\),那么观测值 的条件概率分布 \(z_{k,j}\sim{\mathcal{N}(h(y_i, x_k), Q_{k,j})}\), 对应的(\(x_k\), \(y_i\))的最大似然估计:
\[(x_k, y_i)_{MLE}^* = \\ \\ argmin(\underbrace{(z_{k,j}-h(y_i, x_k))^T\overbrace{Q_{k,j}^{-1}}^{信息矩阵,协方差矩阵的逆}(z_{k,j}-h(y_i, x_k))}_\text{误差项二次型(马氏距离)})
\]
2.2 基于观测数据 \(z\)和输入数据 \(u\)的最小二乘(批量数据)
通常认为观测之间、输入之间、输入和观测之间相互独立,那么进行因式分解:
\[P(z,u|x,y) = \prod_k{P(u_k|x_k, x_{k-1})} \prod_{k,j}P(z_{k,j}|x_k, y_j)
\]
这里将运动误差和观测误差表达如下:
\[\Rightarrow
\]
\[\left\{ \begin{array}{c} e_{v,k}= x_k-f(x_k-1, u_k) \\ e_{z,k,j}=z_{k,j} - h(x_K, y_i)\end{array}\right.
\]
那么目标函数\(J(x,y)\):
\[min(J(x,y))=\sum_k{e^T_{u,k}R^{-1}_ke_{u,k}} + \sum_k\sum_j{e^T_{zk},jQ^{-1}_{k,j}e{z,k,j}}
\]
3 非线性最小二乘
3.1 一阶、二阶梯度法
用F(x)描述最小二乘问题:
\[\underset{x}{min}F(x) = \frac{1}{2}||f(x)||^2 \\
\]
其中, \(x \in \mathbb R\), \(f\)是任意标量非线性函数\(f(x):\mathbb{R}^n \mapsto \mathbb{R}\)
第\(k\)次迭代,在\(x_k\)处,想要寻找增量\(\Delta x_k\),使得目标函数F(x)实现下降。为了简化符号,省略下标k.
\[F(x + \triangle x) \approx F(x) + J(x)^T \triangle x + \frac{1}{2} (\triangle x)^T H(x) \triangle x
\]
\[\triangle x^* = argmin(F(x)+J(X)^T\triangle x + \frac{1}{2}\triangle x^TH\triangle x \\ \downdownarrows \\ \triangle x=-\frac{J}{H}
\]
3.2 高斯牛顿法
不同于牛顿法、最速下降法直接采用\(F(x) = \frac{1}{2}||f(x)||^2\) 进行优化,高斯牛顿法的方法是先对f(x)进行一阶泰勒展开:
\[f(x+\triangle x) \approx f(x) + J(x)^T \triangle x
\]
然后目标是寻找增量\(\triangle x\) ,使得\(||f(x+\triangle x)||^2\)最小。因此可以采用近似的一阶泰勒展开进行最小二乘优化:
\[\begin{align}
\triangle x^*
&= \underset{\triangle x}{argmin} \frac{1}{2}||f(x+\triangle x)||^2 \\
&\approx ||f(x) + J(x)^T \triangle x ||^2 \\
&=\frac{1}{2}({||f(x)||^2+2f(x)J(x)^T\triangle x + \triangle x^TJ(x)J(x)^T\triangle x}) \\ \\
&\downdownarrows{令其求导等于0} \\ \\
&\underbrace{J(x)J(x)^T}_{H(x)}\triangle x = \underbrace{-J(x)f(x) }_{g(x)}
\end{align} \\
\]
这个方程是关于变量的线性方程组,称为增量方程,也可以称为高斯-牛顿方程(Gauss-NewTon equation)或者正规方程(Normal equation):
\[H\triangle x = g
\]
同牛顿法相比,高斯-牛顿法采用\(JJ^T\)近似替代Hessian矩阵,这里求解\(H^{-1}\)需要\(H\)是可逆的。 但是:
① \(H=JJ^T\) 是半正定的,因此会导致增量不稳定,也就是局部不像凸函数,导致算法不收敛;
② 如果步长过大,也会导致局部近似不准确,可能出现不收敛甚至发散。
3.3 列文伯格-马夸尔特法(阻尼牛顿法)
信赖区域方法:在信赖区域中,认为近似是有效的。
\[\rho = \frac{\overbrace{f(x+\triangle x)-f(x)}^{实际下降值} }{\underbrace{J(x)^T \triangle x}_{近似下降值}}
\]
- 若 \(\rho \approx 1\),说明近似效果好;
- 若\(\rho \ll 1\),说明实际减小值远小于近似值,需要缩小近似范围;
- 若\(\rho \gg 1\),说明实际减小值远大于近似值,需要扩大今夕范围求解目标是:
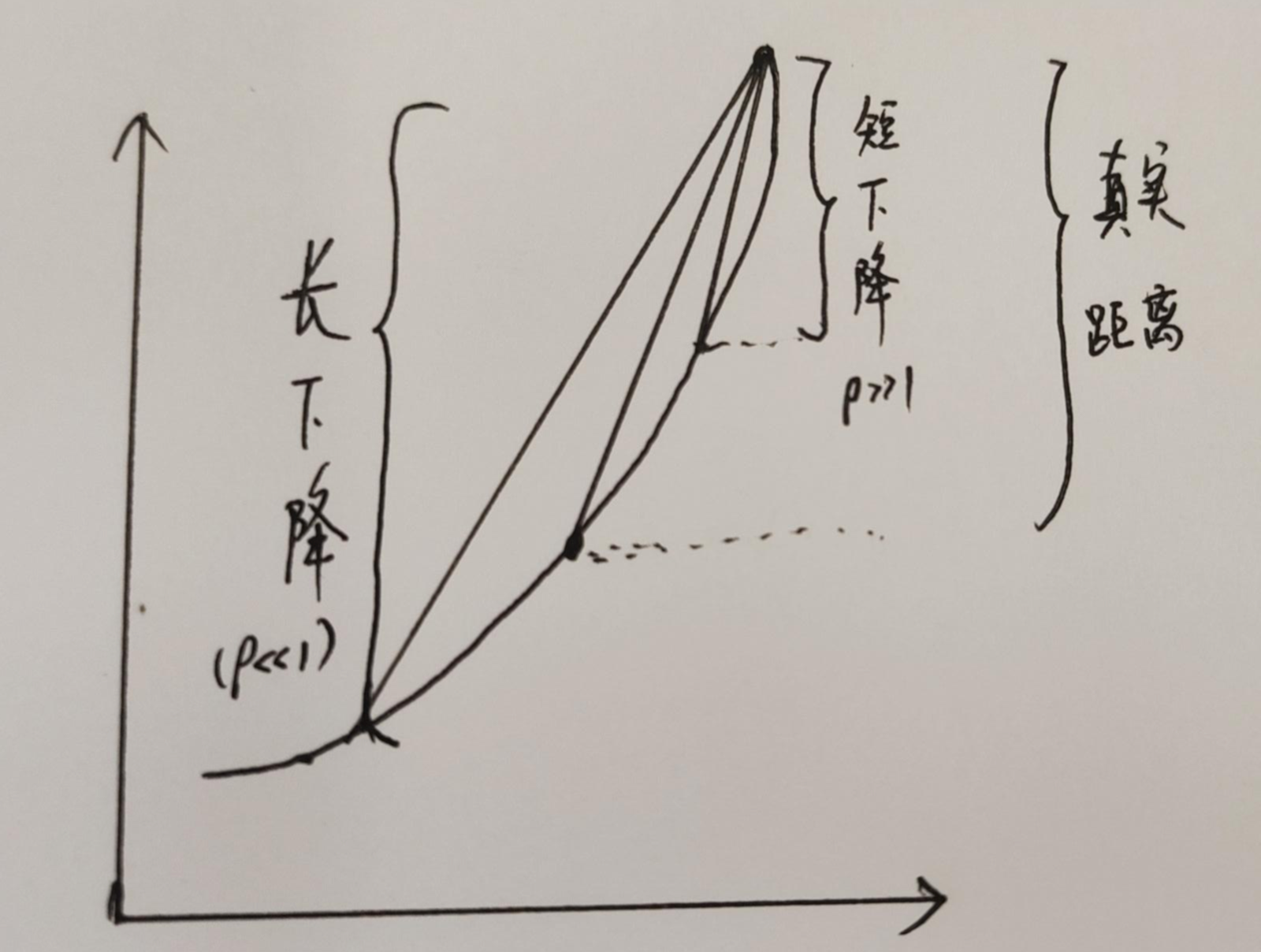
列文伯格-马夸尔特法对非奇异和病态问题,提供了更稳定、准确的增量\(\triangle x\) 计算。


