Latex常用内容
\[X=\left|
\begin{matrix}
x_{11} & x_{12} & \cdots & x_{1d}\\
x_{21} & x_{22} & \cdots & x_{2d}\\
\vdots & \vdots & \ddots & \vdots \\
x_{11} & x_{12} & \cdots & x_{1d}\\
\end{matrix}
\right|
\]
\[\begin{matrix}
1 & x & x^2\\
1 & y & y^2\\
1 & z & z^2\\
\end{matrix}
\]
\[\left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3
\end{array}
\right\}
\]
\[X=\begin{pmatrix}
0&1&1\\
1&1&0\\
1&0&1\\
\end{pmatrix}
\]
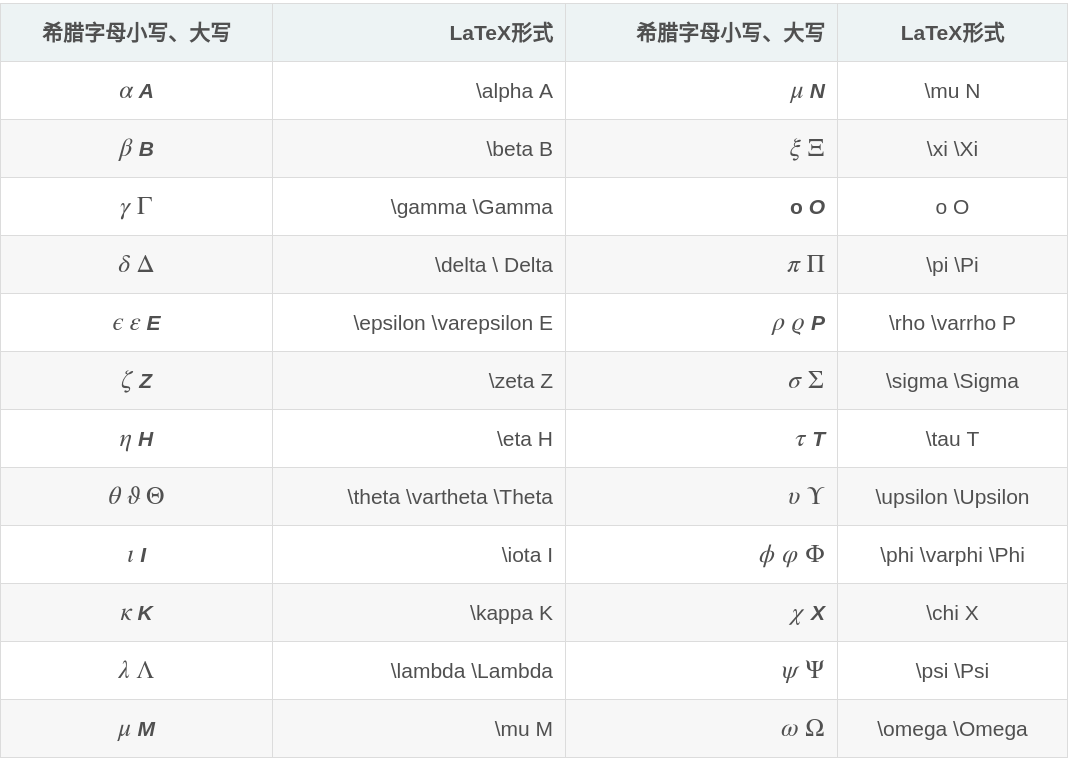
1. 希腊字母表
\Sigma: \(\Sigma\)
\[\begin{align*}
RQSZ \\
\mathcal{RQSZ} \\
\mathfrak{RQSZ} \\
\mathbb{RQSZ}
\end{align*}
\]
\[\begin{align*}
3x^2 \in R \subset Q \\
\mathnormal{3x^2 \in R \subset Q} \\
\mathrm{3x^2 \in R \subset Q} \\
\mathit{3x^2 \in R \subset Q} \\
\mathbf{3x^2 \in R \subset Q} \\
\mathsf{3x^2 \in R \subset Q} \\
\mathtt{3x^2 \in R \subset Q}
\end{align*}
\]
2. 上下标、根号、省略号、空格
下标:_
x^2\(\Longrightarrow\) $ x^2$上标:^
x_i\(\Longrightarrow\) \(x_i\)根号:\sqrt |
y\sqrt{x}\(\Longrightarrow\) \(y\sqrt{x}\)省略号:
\dots\(\Longrightarrow\dots\)
\cdots\(\Longrightarrow\cdots\)
\ddots\(\Longrightarrow\ddots\)括号

| 两个quad空格 | a \qquad b | \(a \qquad b\) | 两个m的宽度 |
|---|---|---|---|
| quad空格 | a \quad b | \(a \quad b\) | 一个m的宽度 |
| 大空格 | a\ b | \(a\ b\) | 1/3m宽度 |
| 中等空格 | a;b | \(a\;b\) | 2/7m宽度 |
| 小空格 | a,b | \(a\,b\) | 1/6m宽度 |
| 没有空格 | ab | \(ab\) | |
| 紧贴 | a!b | \(a\!b\) | 缩进1/6m宽度 |
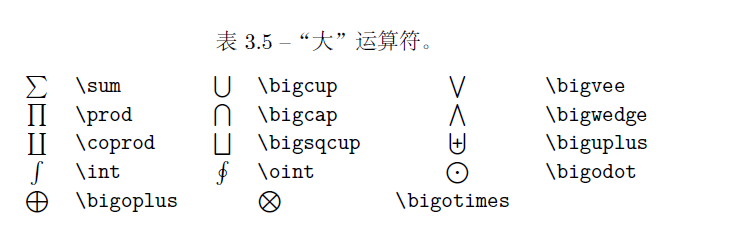
3. 运算符
- 求和:
\sum_1^n\(\Longrightarrow\) \(\sum_1^n\)- 积分:
\int_1^n\(\Longrightarrow\) \(\int_1^n\)- 极限:
lim_{x \to \infty}\(\Longrightarrow\) \(lim_{x \to \infty}\)- 分数:
\frac{2}{3}\(\Longrightarrow\) $\frac{2}{3} $- 开方:\sqrt[2]{x} \(\Longrightarrow\) \(\sqrt[2]{x}\)
- 积 :\prod_{i=0}^n \(\Longrightarrow\) \(\prod_{i=0}^n\)













f4. 箭头

| 字符 | 含义 |
|---|---|
| \uparrow | ↑ |
| \downarrow | ↓ |
| \Uparrow | ⇑ |
| \Downarrow | ⇓ |
| \updownarrow | ↕ |
| \Updownarrow | ⇕ |
| \rightarrow | → |
| \leftarrow | ← |
| \Rightarrow | ⇒ |
| \Leftarrow | ⇐ |
| \leftrightarrow | ↔ |
| \Leftrightarrow | ⇔ |
| \longrightarrow | ⟶ |
| \longleftarrow | ⟵ |
| \Longrightarrow | ⟹ |
| \Longleftarrow | ⟸ |
| \mapsto | ↦ |
| \longmapsto | ⟼ |
| \hookleftarrow | ↩ |
| \hookrightarrow | ↪ |
| \leftharpoonup | ↼ |
| \rightharpoonup | ⇀ |
| \leftharpoondown | ↽ |
| \rightharpoondown | ⇁ |
| \rightleftharpoons | ⇌ |
| \leadsto | ⇝ |
| \nearrow | ↗ |
| \searrow | ↘ |
| \swarrow | ↙ |
| \nwarrow | ↖ |
| \nleftarrow | ↚ |
| \nrightarrow | ↛ |
| \nLeftarrow | ⇍ |
| \nRightarrow | ⇏ |
| \nleftrightarrow | ↮ |
| \nLeftrightarrow | ⇎ |
| \dashrightarrow | ⇢ |
| \dashleftarrow | ⇠ |
| \leftleftarrows | ⇇ |
| \leftrightarrows | ⇆ |
| \Lleftarrow | ⇚ |
| \twoheadleftarrow | ↞ |
| \leftarrowtail | ↢ |
| \looparrowleft | ↫ |
| \leftrightharpoons | ⇋ |
| \curvearrowleft | ↶ |
| \circlearrowleft | ↺ |
| \Lsh | ↰ |
| \upharpoonleft | ↿ |
| \downharpoonleft | ⇃ |
| \upuparrows | ⇈ |
| \multimap | ⊸ |
| \leftrightsquigarrow | ↭ |
| \rightrightarrows | ⇉ |
| \rightleftarrows | ⇄ |
| \twoheadrightarrow | ↠ |
| \rightarrowtail | ↣ |
| \looparrowright | ↬ |
| \rightleftharpoons | ⇌ |
| \curvearrowright | ↷ |
| \circlearrowright | ↻ |
| \Rsh | ↱ |
| \downdownarrows | ⇊ |
| \upharpoonright | ↾ |
| \downharpoonright | ⇂ |
| \rightsquigarrow | ⇝ |
5. 分段函数
f(n)=
\begin{cases}
n/2, & \text{if $n$ is even}\\
3n+1,& \text{if $n$ is odd}
\end{cases}
\[f(n)=
\begin{cases}
n/2, & \text{if $n$ is even}\\
3n+1,& \text{if $n$ is odd}
\end{cases}
\]
6. 方程组
\left.
\left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3
\end{array}
\right.
\right>
\[ \left.
\left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3
\end{array}
\right.
\right>
\]
7.矩阵
7.1 基本语法
- 起始标记
\begin{matrix},结束标记\end{matrix}- 每一行末尾标记
\\- 行间元素之间用
&分隔。
\begin{matrix}
0&1&1\\
1&1&0\\
1&0&1\\
\end{matrix}
\[ \begin{matrix}
0&1&1\\
1&1&0\\
1&0&1\\
\end{matrix}
\]
7.2 矩阵边框
- 在起始、结束标记用下列词替换
matrixpmatrix:小括号边框bmatrix:中括号边框Bmatrix:大括号边框vmatrix:单竖线边框Vmatrix:双竖线边框
\begin{vmatrix}
0&1&1\\
1&1&0\\
1&0&1\\
\end{vmatrix}
\[\begin{vmatrix}
0&1&1\\
1&1&0\\
1&0&1\\
\end{vmatrix}
\]
7.3 省略元素
- 横省略号:
\cdots- 竖省略号:
\vdots- 斜省略号:
\ddots
\begin{bmatrix}
{a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\
{a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
{a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\
\end{bmatrix}
\[\begin{bmatrix}
{a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\
{a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
{a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\
\end{bmatrix}
\]
7.4 阵列
- 需要array环境:起始、结束处以{array}声明
- 对齐方式:在{array}后以{}逐行统一声明
- 左对齐:
l居中:c右对齐:r- 竖直线:在声明对齐方式时,插入
|建立竖直线- 插入水平线:
\hline
\begin{array}{c|lll}
{↓}&{a}&{b}&{c}\\
\hline
{R_1}&{c}&{b}&{a}\\
{R_2}&{b}&{c}&{c}\\
\end{array}
\[\begin{array}{c|lll}
{↓}&{a}&{b}&{c}\\
\hline
{R_1}&{c}&{b}&{a}\\
{R_2}&{b}&{c}&{c}\\
\end{array}
\]
8.常用公式
8.1 线性模型
h(\theta) = \sum_{j=0} ^n \theta_j x_j
\[h(\theta) = \sum_{j=0} ^n \theta_j x_j
\]
8.2 均方误差
J(\theta) = \frac{1}{2m}\sum_{i=0}^m(y^i - h_\theta(x^i))^2
\[J(\theta) = \frac{1}{2m}\sum_{i=0}^m(y^i - h_\theta(x^i))^2
\]
8.3 求积
H_c=\sum_{l_1+\dots +l_p}\prod^p_{i=1} \binom{n_i}{l_i}
\[H_c=\sum_{l_1+\dots +l_p}\prod^p_{i=1} \binom{n_i}{l_i}
\]
8.4 批梯度下降
\[\frac{\partial J(\theta)}{\partial\theta_j} = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i))x^i_j
\]
\[\begin{align}
\frac{\partial J(\theta)}{\partial\theta_j}
& = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(y^i-h_\theta(x^i))\\
& = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(\sum_{j=0}^n\theta_j x^i_j-y^i)\\
&=-\frac1m\sum_{i=0}^m(y^i -h_\theta(x^i)) x^i_j
\end{align}
\]
8.5 贝叶斯、先验、后验估计、似然估计
\[\begin{align}
\overbrace{P(x,y|z,u)}^{后验概率}
&= \frac{P(z,u|x,y)P(x,y)}{P(z,u)}\\
&\approx \underbrace{P(z,u|x,y)}_{似然} \ \underbrace{P(x,y)}_{先验概率}
\end{align}
\]
\[\begin{align}
(x,y)^*_{MAP}
&=argmax{P(x,y∣z,u)} \\
&=argmax{\frac{P(z,u|x,y)P(x,y)}{\underbrace{P(z,u)}_{此项与x,y无关,可以去掉}}} \\
&=argmax{{P(z,u|x,y)P(x,y)}}
\end{align}
\]
8.6 任意维高斯分布
\[P(x)=\frac{1}{\sqrt{(2\pi)^Ndet(\Sigma)}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) \\
\Downarrow\Downarrow\Downarrow 负对数\\
-ln(P(x)) = \frac{1}{2}ln((2\pi)^Ndet(\Sigma))+\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) \\
\Downarrow\Downarrow\Downarrow 负对数\\
(x)^*_{MLE}=argmax(P(x))=argmin((x-\mu)^T\Sigma^{-1}(x-\mu))
\]
8.7 高斯牛顿法求导
\[\begin{align}
\triangle x^*
&= \underset{\triangle x}{argmin} \frac{1}{2}||f(x+\triangle x)||^2 \\
&\approx ||f(x) + J(x)^T \triangle x ||^2 \\
&=\frac{1}{2}({||f(x)||^2+2f(x)J(x)^T\triangle x + \triangle x^TJ(x)J(x)^T\triangle x}) \\ \\
&\downdownarrows{令其求导等于0} \\ \\
&\underbrace{J(x)J(x)^T}_{H(x)}\triangle x = \underbrace{-J(x)f(x) }_{g(x)}
\end{align} \\
\]
引用:

