机器学习 | 吴恩达斯坦福课程笔记整理之(三)神经网络
本系列为吴恩达斯坦福CS229机器学习课程笔记整理,以下为笔记目录:
(一)线性回归
(二)逻辑回归
(三)神经网络
(四)算法分析与优化
(五)支持向量机
(六)K-Means
(七)特征降维
(八)异常检测
(九)推荐系统
(十)大规模机器学习
第三章 神经网络
一、再论0/1分类问题
通过对特征进行多项式展开,可以让逻辑回归支持非线性的分类问题。
假定我们现在有 n 维特征,需要进行非线性分类,采用二次多项式扩展特征后,特征个数就为 n+C2n≈n22 个特征,特征的空间复杂度就为 O(n2) ,如果扩展到三次多项式,则空间复杂度能达到 O(n3) 。
因此需要考虑用新的机器学习模型来处理高维特征的非线性分类问题,神经网络是典型的不需要增加特征数目就能完成非线性分类问题的模型。
二、神经网络概述
· 人体神经元模型
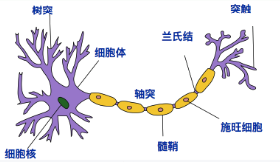
接收区(receptive zone):树突接收到输入信息。
触发区(trigger zone):位于轴突和细胞体交接的地方,决定是否产生神经冲动。
传导区(conducting zone):由轴突进行神经冲动的传递。
输出区(output zone):神经冲动的目的就是要让神经末梢,突触的神经递质或电力释出,才能影响下一个接受的细胞(神经元、肌肉细胞或是腺体细胞),此称为突触传递。
· 人工神经网络
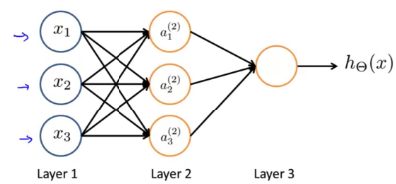
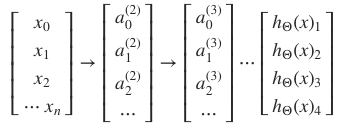
输入层:输入层接收特征向量 x 。
输出层:输出层产出最终的预测 h 。
隐含层:隐含层介于输入层与输出层之间,之所以称之为隐含层,是因为当中产生的值并不像输入层使用的样本矩阵 X 或者输出层用到的标签矩阵 y 那样直接可见。
二、前向传播与反向传播
· 前向传播
神经网络每层都包含有若干神经元,层间的神经元通过权值矩阵 Θl 连接。一次信息传递过程可以如下描述:
- 第 j 层神经元接收上层传入的刺激(神经冲动);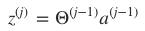
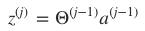
- 该刺激经激励函数(activation function)g 作用后,会产生一个激活向量 aj 。 aji 表示的就是 j 层第 i 个神经元获得的激活值(activation):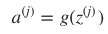
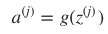
刺激由前一层传向下一层,故而称之为前向传递
对于非线性分类问题,逻辑回归会使用多项式扩展特征,导致维度巨大的特征向量出现,而在神经网络中,并不会增加特征的维度,即不会扩展神经网络输入层的规模,而是通过增加隐含层,矫正隐含层中的权值,来不断优化特征,前向传播过程每次在神经元上产出的激励值都可看做是优化后的特征。

· 代价函数

矩阵表示
其中, .∗ 代表点乘操作,A∈R(K×m) 为所有样本对应的输出矩阵,其每一列对应一个样本的输出, Y∈R(m×K) 为标签矩阵,其每行对应一个样本的类型。
· 反向传播
由于神经网络允许多个隐含层,即,各层的神经元都会产出预测,因此,就不能直接利用传统回归问题的梯度下降法来最小化 J(Θ) ,而需要逐层考虑预测误差,并且逐层优化。用反向传播法优化预测。首先定义各层的预测误差为向量 δ(l) :
反向传播中的反向二字也正是从该公式中得来,本层的误差 δ(l) 需要由下一层的误差 δ(l+1) 反向推导。
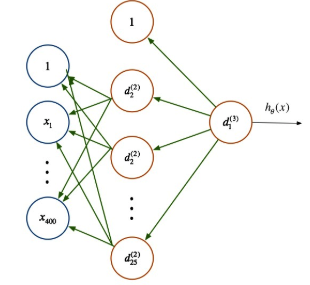
· 训练过程

三、参数展开
需要先将矩阵元素平铺开为一个长向量
四、梯度校验(Gradient Checking)
BP算法检验
五、权值初始化
· 0值初始化
隐含层的神经元激活值将一样,各层只有一个有效神经元,失去神经网络进行特征扩展和优化的本意
· 随机初始化
六、感知器
最简单的神经网络结构,不包含隐含层
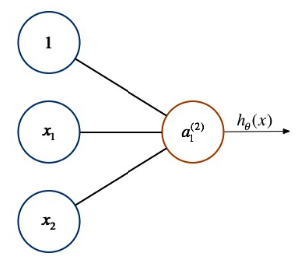
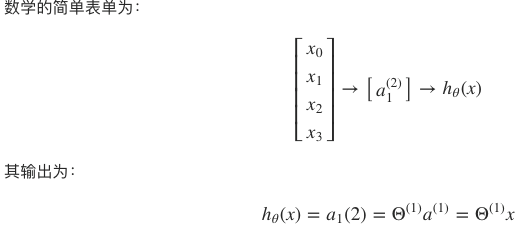
从形式上看,回归问题算是感知器的非网络表达形式。
感知器可以解决逻辑运算问题(01分类问题)-sigmoid函数
多分类问题,添加多个隐层
七、神经网络训练过程
· 神经网络设计
在神经网络的结构设计方面,往往遵循如下要点:
- 输入层的单元数等于样本特征数。
- 输出层的单元数等于分类的类型数。
- 每个隐层的单元数通常是越多分类精度越高,但是也会带来计算性能的下降,因此,要平衡质量和性能间的关系。
- 默认不含有隐藏层(感知器),如果含有多个隐层,则每个隐层上的单元数最好保持一致。
· 过程
- 设计激活函数
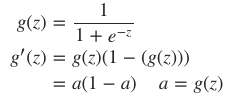
- 设计初始化权值矩阵的函数
- 定义参数展开和参数还原函数
Args: hiddenNum 隐层数目
unitNum 每个隐层的神经元数目
inputSize 输入层规模
classNum 分类数目
epsilon epsilon
Returns:
Thetas 权值矩阵序列
- 定义梯度校验过程
Args:
Thetas 权值矩阵
X 样本
y 标签
theLambda 正规化参数
Returns:
checked 是否检测通过
- 计算代价函数
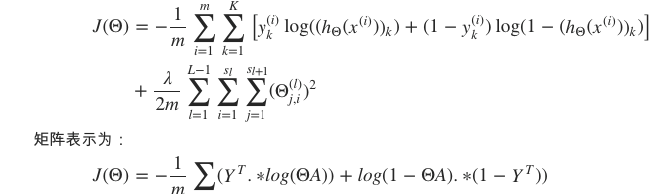
Args:
Thetas 权值矩阵序列
X 样本
y 标签集
a 各层激活值
Returns:
J 预测代价 """
- 设计前向传播过程
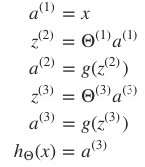
"""前向反馈过程
Args:
Thetas 权值矩阵
X 输入样本
Returns:
a 各层激活向量 """
- 设计反向传播过程
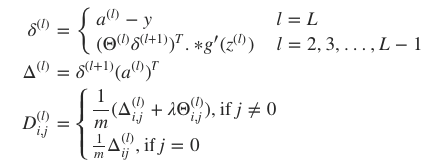
1)计算梯度
Args:
a 激活值
y 标签
Returns:
D 权值梯度
2)获得梯度后,更新权值
"""更新权值
Args:
m 样本数
Thetas 各层权值矩阵
D 梯度
alpha 学习率
theLambda 正规化参数
Returns:
Thetas 更新后的权值矩阵 """
综上,我们能得到梯度下降过程:
前向传播计算各层激活值;
反向计算权值的更新梯度;
更新权值;
训练结果将包含如下信息:(1)网络的预测误差 error;(2)各层权值矩阵 Thetas;(3)迭代次数 iters;(4)是否训练成功 success。
最后通过预测函数
"""预测函数
Args:
X: 样本
Thetas: 训练后得到的参数
Return: a """

