机器学习 | 吴恩达斯坦福课程笔记整理之(一)线性回归
本系列为吴恩达斯坦福CS229机器学习课程笔记整理,以下为笔记目录:
(一)线性回归
(二)逻辑回归
(三)神经网络
(四)算法分析与优化
(五)支持向量机
(六)K-Means
(七)特征降维
(八)异常检测
(九)推荐系统
(十)大规模机器学习
第一章 线性回归
一、ML引言
- 学习行为,定制服务
- 监督学习和非监督学习
- 了解应用学习算法的实用建议
1.3 监督学习
- 基本思想:数据集中的每个样本都有相应的“正确答案”。再根据这些样本作出预测。
- 连续变量-回归,离散变量-分类;
1.4 非监督学习
- 无标签
- 聚类算法
- 从数据中找到某种结构
二、回归问题
- 步骤:积累知识(training set)-> 学习(learning algorithm)->预测(对应关系)
三、线性回归与梯度下降
- 预测
特征,特征向量,输出向量,假设hypothesis(预测函数)
而称为回归方程,θ 为回归系数
- 误差评估
评估各个真实值 y(i) 与预测值 hθ(x(i)) 之间的差异 -> 最小均方(Least Mean Square)
也称为代价函数(Cost function)
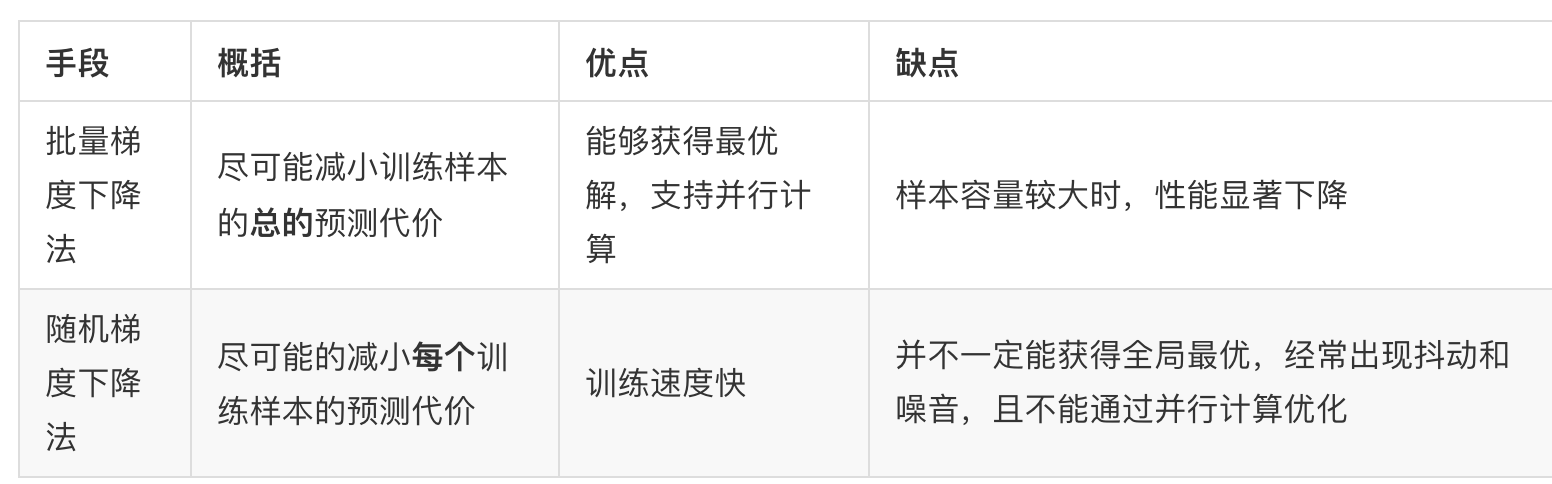
- 批量梯度下降BGD
学习效果不好时,纠正学习策略
目标:反复调节 θ 使得预测 J(θ) 足够小 -> 梯度下降(Gradient Descent)
沿着梯度方向,接近最小值。
对于一个样本容量为 m 的训练集,我们定义 θ 的调优过程为:重复直到收敛(Repeat until convergence),该过程为基于最小均方(LMS)的批量梯度下降法(Batch Gradient Descent)
但是每调节一个θj ,都要历一遍样本集,如果样本的体积m很大,开销巨大
- 随机梯度下降(Stochastic Gradient Descent, SGD):样本量巨大时,迅速获得最优解
四、正规方程
为求得 J(θ) 的最小值,通过正规方程来最小化 J(θ) :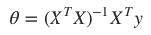
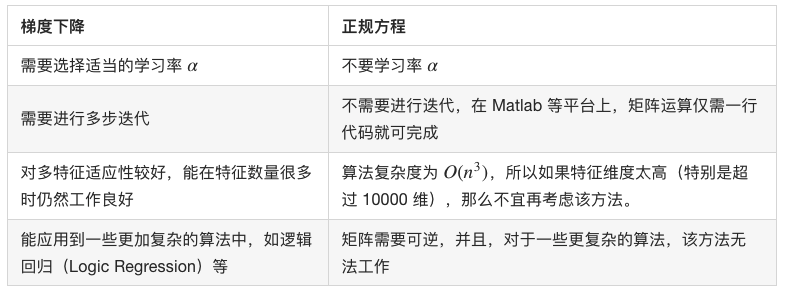
摆脱了学习率的束缚,但只适合于低维向量
五、特征缩放
将各个特征量化到统一的区间,两种量化方式:
1)Standardization
又称为 Z-score normalization,量化后的特征将服从标准正态分布:
其中, μ, δ 分别为对应特征 xi 的均值和标准差。量化后的特征将分布在 [−1,1] 区间。
2)Min-Max Scaling
又称为 normalization
量化后的特征将分布在 [0,1] 区间。
六、多项式回归
方程中添加高阶项,提高拟合效果
七、欠拟合和过拟合
- 欠拟合(underfitting):拟合程度不高,数据距离拟合曲线较远。
- 过拟合(overfitting):过度拟合,貌似拟合几乎每一个数据,但是丢失了信息规律。
为了解决欠拟合和过拟合问题,引入了局部加权线性回归(Locally Weight Regression)。

在 LWR 中,我们对一个输入 x 进行预测时,赋予了 x 周围点不同的权值,距离 x 越近,权重越高。整个学习过程中误差将会取决于 x 周围的误差,而不是整体的误差,这也就是局部一词的由来。
通常, w(i) 服从高斯分布,在 x 周围呈指数型衰减: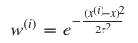
其中, τ 值越小,则靠近


