递归详解

递归的定义

定义：递归算法是一种直接或者间接调用自身函数或者方法的算法。

通俗来说，递归算法的实质是把问题分解成规模缩小的同类问题的子问题，然后递归调用方法来表示问题的解。它有如下特点：

• 一个问题的解可以分解为几个子问题的解
• 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
• 存在递归终止条件，即必须有一个明确的递归结束条件，称之为递归出口

数学代入法理解递归

假设我们用递归来算阶乘 f(n)

f = n =>
    n === 1 ? 1
            : n * f(n-1) 

f 里面用到了 f，怎么理解呢？

很简单，把式子展开即可：

 看到递归了吗？

先递进，在回归--这就是递归。

以上是SICP原文（有删改）

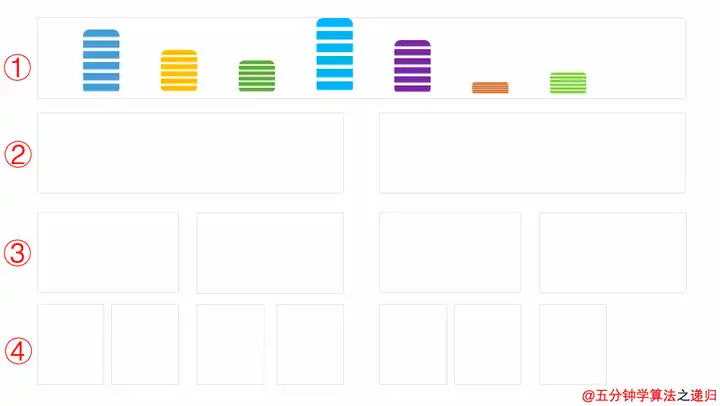
归并排序递归详解

f({8, 6, 8, 4, 2, 3})
=> f(fl({8, 6, 8}) fr({4, 2, 3}))
=> f(fl(fl({8, 6})fr({8})) fr({4, 2, 3}))
=> f(fl(fl(fl({8})fr({6}))fr({8})) fr({4, 2, 3}))
=> f(fl(fl({6, 8})fr({8})) fr({4, 2, 3}))
=> f(fl({6, 8, 8}) fr(fl({4, 2})fr({3})))
=> f(fl({6, 8, 8}) fr(fl(fl({4})fr({2}))fr(3)))
=> f(fl({6, 8, 8}) fr(fl({2, 4})fr({3})))
=> f(fl({6, 8, 8}) fr({2, 3, 4}))
=> f({2, 3, 4, 6, 8, 8})

 

 先递归左，在递归右，当递归到最后一个元素之后，看是交换位置。