归并排序

1.归并排序详解

1.1核心思想

归并排序是一种基于分而治之的排序技术。最坏情况下的时间复杂度为O(nlogn），它是最受人尊敬的算法之一。归并排序首先将数组分成相等的两半，然后以排序的方式将它们合并。

为了理解合并排序，我们采用未排序的数组，如下所示

我们知道归并排序首先将整个数组迭代地分成相等的一半，除非获得原子值。我们在这里看到一个由8个项目组成的数组分为两个大小为4的数组。

这不会更改原件中项目出现的顺序。现在我们将这两个数组分为两半。

我们进一步划分这些数组，并获得无法再划分的原子值

现在，我们将它们分解时的方式完全相同。请注意提供给这些列表的颜色代码。

我们首先比较每个列表的元素，然后以排序的方式将它们组合到另一个列表中。我们看到14和33处于排序位置。我们比较27和10，在2个值的目标列表中，我们先放置10，然后是27。我们更改19和35的顺序，而将42和44顺序放置。

在合并阶段的下一个迭代中，我们比较两个数据值的列表，然后将它们合并为找到的数据值的列表，将所有数据按排序顺序放置。

最终合并后，列表应如下所示：

1.2代码思路

首先我们来看看两个顺序表是如何变成一个有序表的，实际上做法就是将两个指针指向两个数组，然后进行比较，看那个指针指向的数据小，将小的数据插入新的数组里，然后将这个指针加1如图所示。

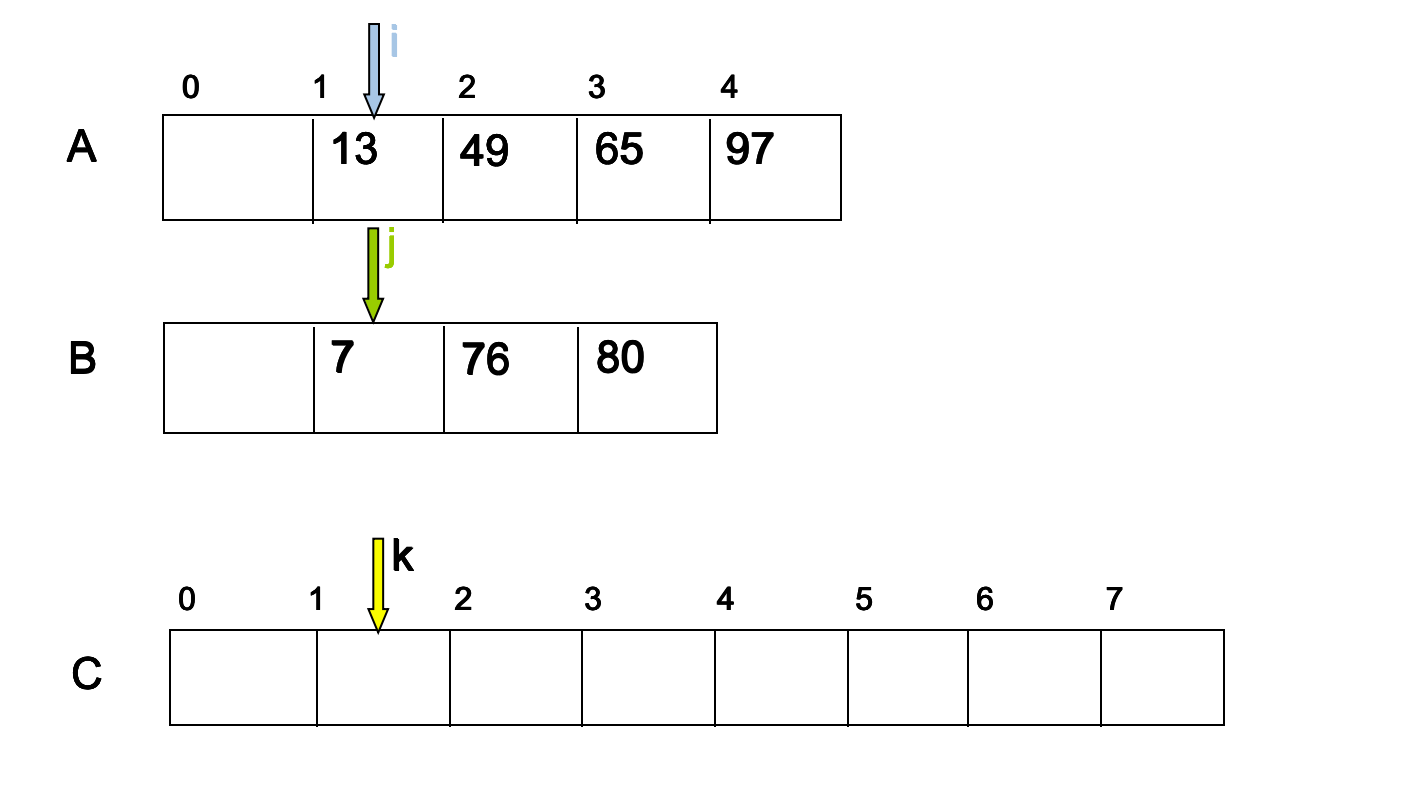
 过程

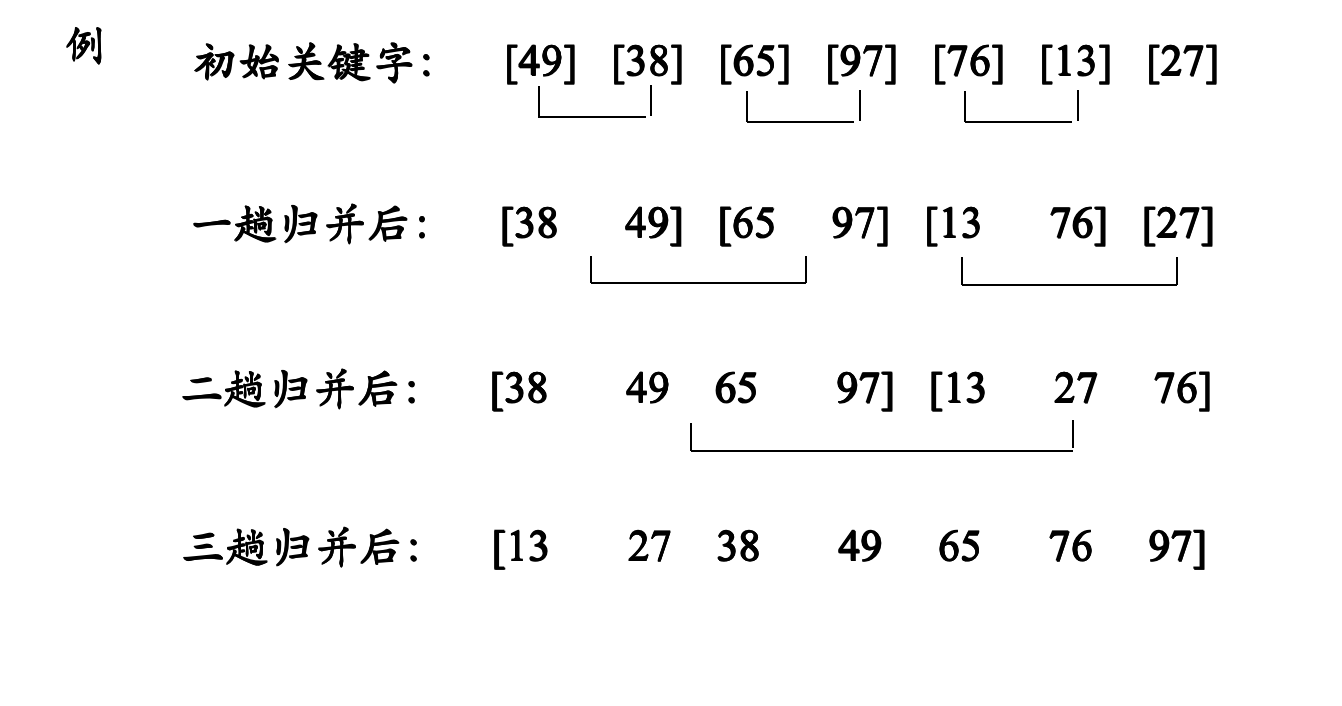
 可以看出这个过程，每次两两进行比较的时候，都可以表示是两个有序的数组，变成一个有序数组的过程。经过数次的变化，就好变成排序状态的数组。

2.代码示例

import java.util.Arrays;

/**
 * @author 民宿
 * @dscription 归并排序
 */
public class MergeSort1 {
    public static void main(String[] args) {
        int[] arr = new int[]{8, 6, 8, 4, 2};
        mergeSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 归并排序
     *
     * @param arr 无序数组
     */
    private static void mergeSort(int[] arr, int left, int right) {
        int mid = left + ((right - left) >> 1);
        if (left < right) {
            // 左边
            mergeSort(arr, left, mid);
            // 右边
            mergeSort(arr, mid + 1, right);
            // 左右归并
            merge(arr, left, mid, right);
        }
    }

    /**
     * @param arr   无序数组
     * @param left  左指针
     * @param mid   中间指针
     * @param right 右指针
     */
    private static void merge(int[] arr, int left, int mid, int right) {
        // 左指针
        int i = left;
        // 右指针
        int j = mid + 1;
        // 临时数组
        int[] temp = new int[right - left + 1];
        // 临时数组指针
        int k = 0;


        // 把较小的数移到临时数组中
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                temp[k] = arr[i];
                i++;
                k++;
            } else {
                temp[k] = arr[j];
                j++;
                k++;
            }
        }

        // 把左边剩余的数移入临时数组
        while (i <= mid) {
            temp[k] = arr[i];
            i++;
            k++;
        }

        // 把右边剩余的数移入临时数组
        while (j <= right) {
            temp[k] = arr[j];
            j++;
            k++;
        }

        // 把临时数组覆盖原数组
        for (int m = 0; m < temp.length; m++) {
            arr[m + left] = temp[m];
        }
    }
}

3.算法复杂度

平均时间复杂度	O(nlogn)
最坏时间复杂度	O(nlogn)
最优时间复杂度	O(nlogn)
空间复杂度	O(N)
最佳解	有时是

比较操作的次数介于(nlogn)/n和nlogn - n + 1。 赋值操作的次数是2nlogn。归并算法的空间复杂度为：O(N)