[ROS学习] 13.ROS中的坐标管理系统

笔记参考【ROS学习笔记】13.ROS中的坐标管理系统
内容参考：基于B站ROS公开课：【古月居】古月·ROS入门21讲

本节说明

本节学习ROS中的坐标管理系统。介绍坐标之间的相互转换方法。

1 机器人中的坐标变换

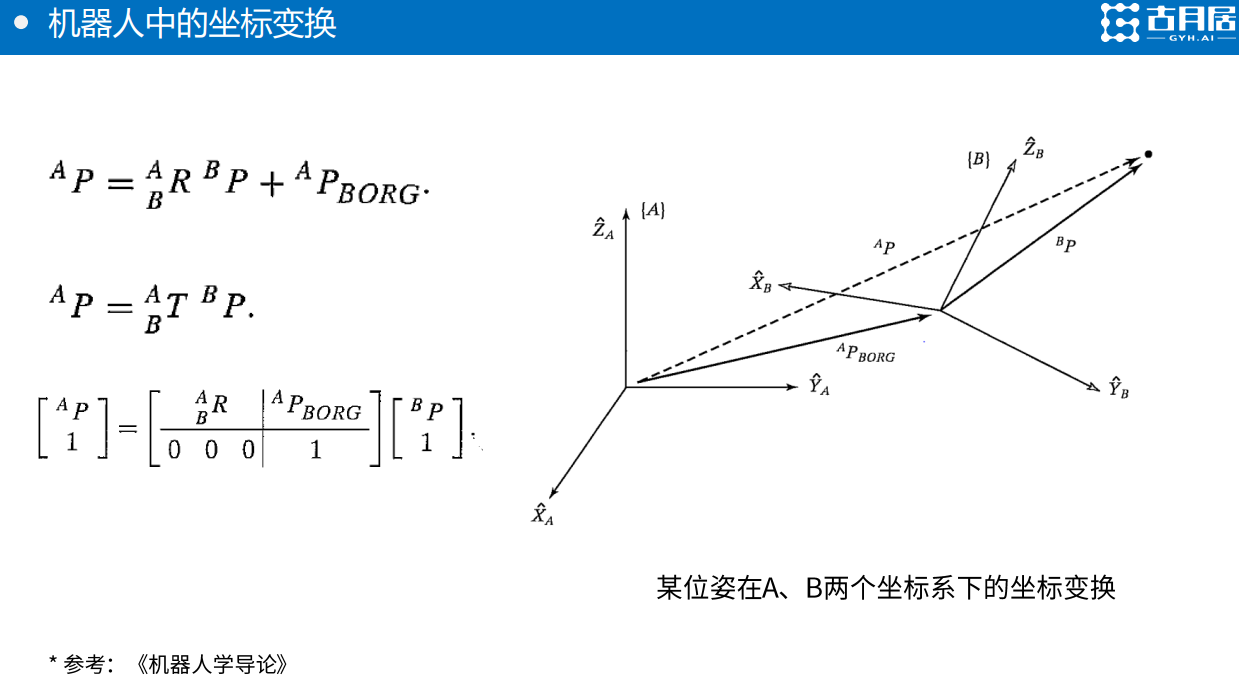
机器人运动学的核心，描述任意两个坐标系之中任意两个向量之间的变换，可以用一个4×4的变换矩阵（Transformation Matrices）来描述它的平移和旋转变化。
变换矩阵中有包括旋转矩阵（Rotation Matrix）的信息和位置移动（Translation）的信息。

参考笔记中博主推荐：B站的机器人学入门课程：台大机器人学之运动学——林沛群。

2 TF功能包

一个机器人中，可以有很多坐标系，我们需要去描述任意两个坐标系之间的关系，涉及到大量的矩阵运算。我们可以用ROS中的TF(Transform)功能包来解决问题。

TF功能包的特点：默认能记录10秒内机器人所有坐标系之间的位置关系。

能具体了解什么信息呢？举个栗子：

• 5秒钟之前，机器人头部坐标系相对于全局坐标系的关系是什么样的？
• 机器人夹取的物体相对于机器人中心坐标系的位置在哪里？
• 机器人中心坐标系相对于全局坐标系的位置在哪里？

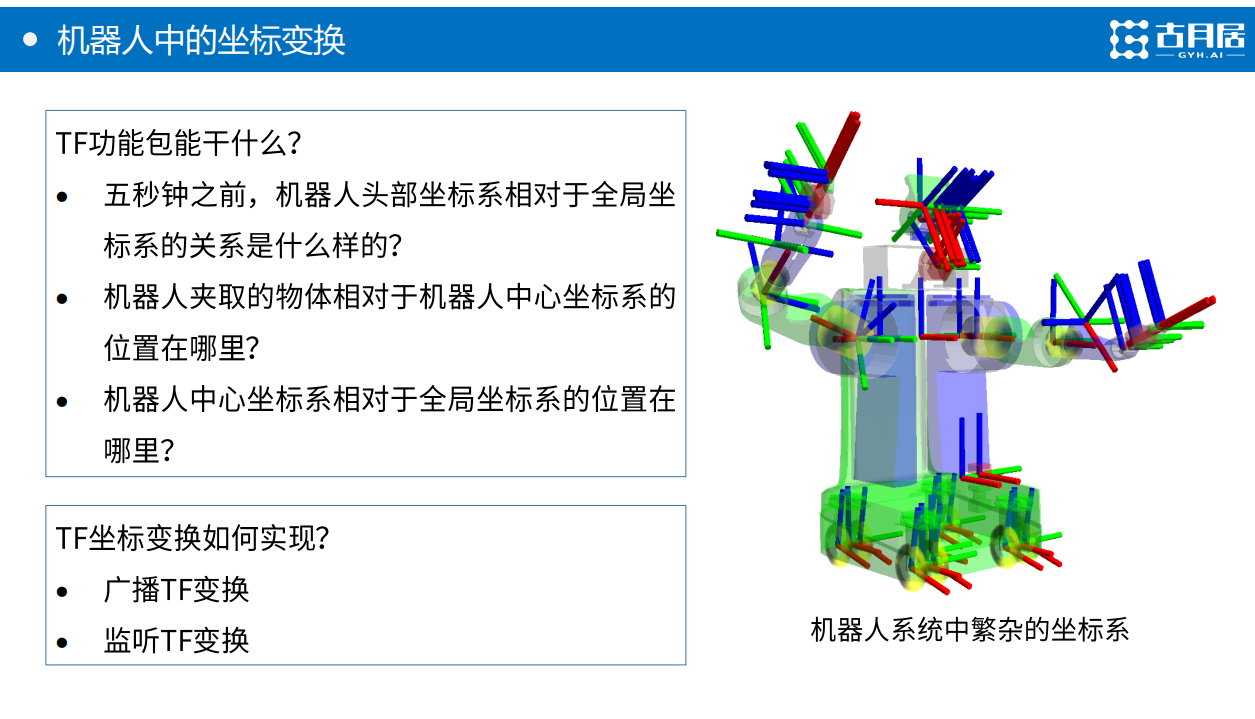
TF坐标变换如何实现？

实现机制：

• 广播TF变换
• 监听TF变换

这有别于之前topic和service的机制。广播和监听的具体实现会在下一节讲解。
在ROS Master启动后，启动TF后，会在后台维护一个名为“TF树（TF Tree）”的数据结构。所有的坐标系都是通过树形结构保存在这个树结构当中，当有结点想查询某两个坐标系之间的关系的话，直接可以查询这个TF Tree来得到。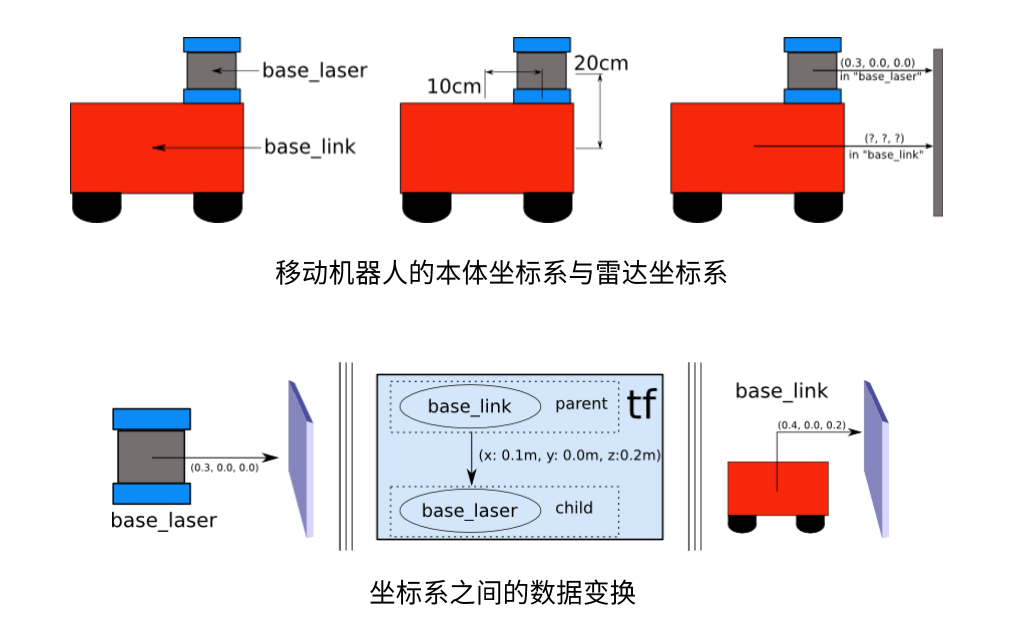

比如这辆带激光雷达的车，车体是以base_link为坐标系的，激光雷达是以base_laser为坐标系的，可以看到base_laser是base_link向x轴平移了0.1m，向z轴平移了0.2m，y轴没有平移。
当base_laser测到离墙面的距离为0.3m，即向量(0.3,0,0)时，就可以根据图下方的TF tree进行坐标系之间的数据变换的运算，从而算出base_link的相对与测距点的相对向量(0.4,0,0.2)。

3 小程序：小海龟跟随实验

我们通过一个小程序来实现一个小海龟跟随另一个小海龟，并通过可视化的方法以理解坐标系的变换。

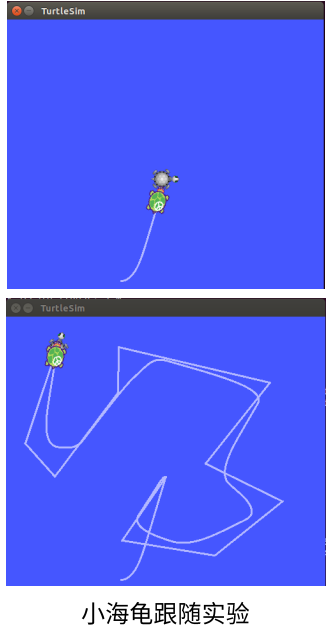
打开小程序

接着我们正式打开小程序:

roslaunch turtle_tf turtle_tf_demo.launch

 

打开后就会有两只海龟，我们直接用键盘操作一只海龟前进，另一只会跟过来。

rosrun turtlesim turtle_teleop_key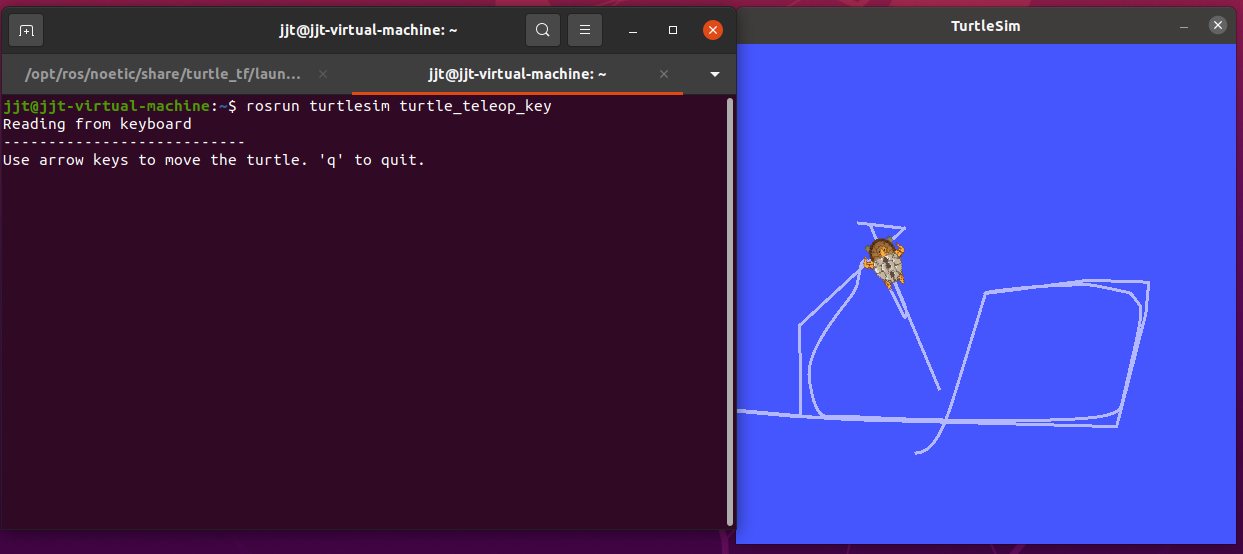

查看当前的TF树

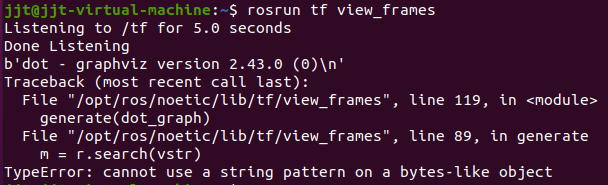
我们来查看当前的TF tree，查看一下坐标系之间的关系。

rosrun tf view_frames

程序报错了，没法生成PDF文件。我们按照报错修改一下文件。

我们先打开它指向的那个view_frames文件的修改权限：

sudo chmod a+w /opt/ros/noetic/lib/tf/view_frames

然后去对应目录下打开文件，88行后加上这句vstr = str(vstr)：

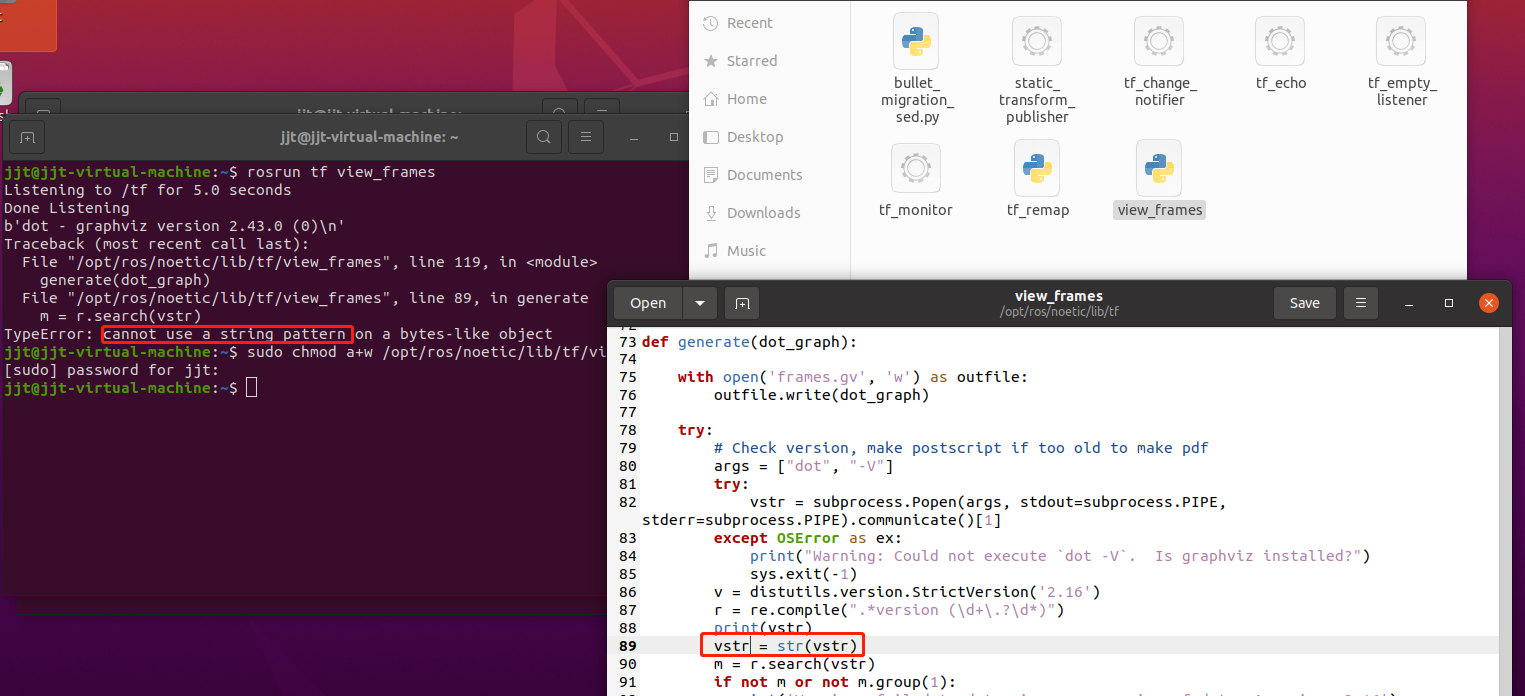
再运行：

rosrun tf view_frames

可在用户文件夹下生成一个pdf文件：
可以看到有3个坐标系，除了两个海龟自身的坐标系，还有个world坐标系。
这颗TF树展示了当前的坐标间的位置关系，turtle1和turtle2是相对world坐标系变化的。

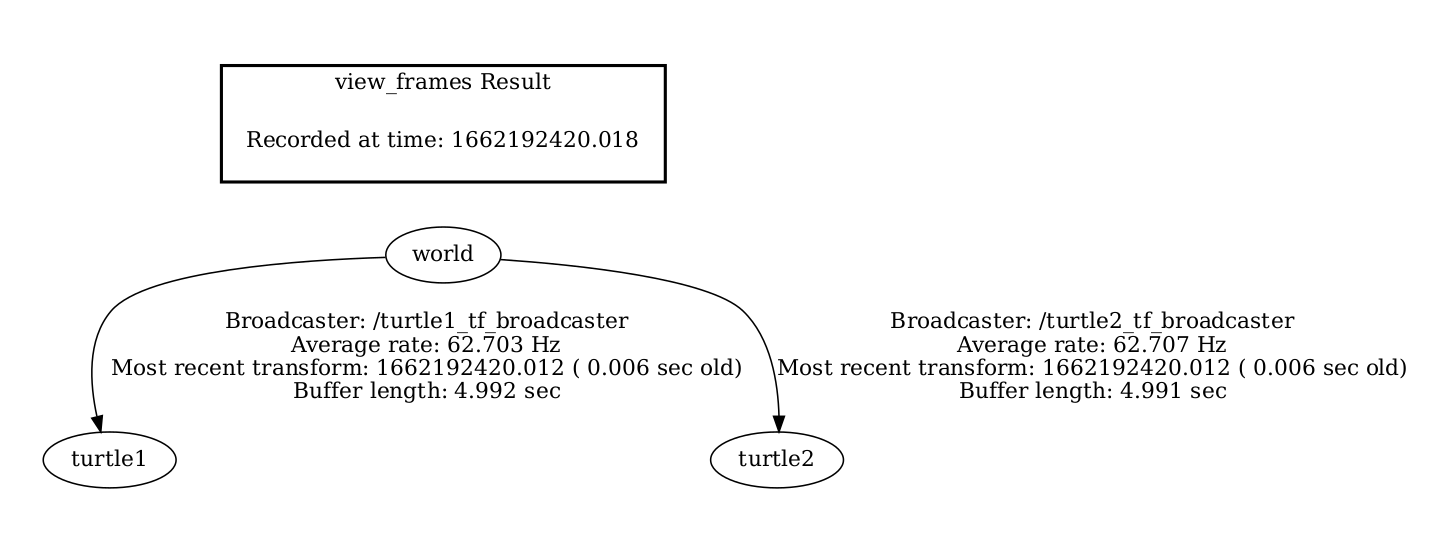
坐标相对位置关系可视化1（tf_echo）

比如我们想看两个海龟的相对变换关系，直接输入：

rosrun tf tf_echo turtle1 turtle2

操控海龟1移动，相对关系就发生了变化：

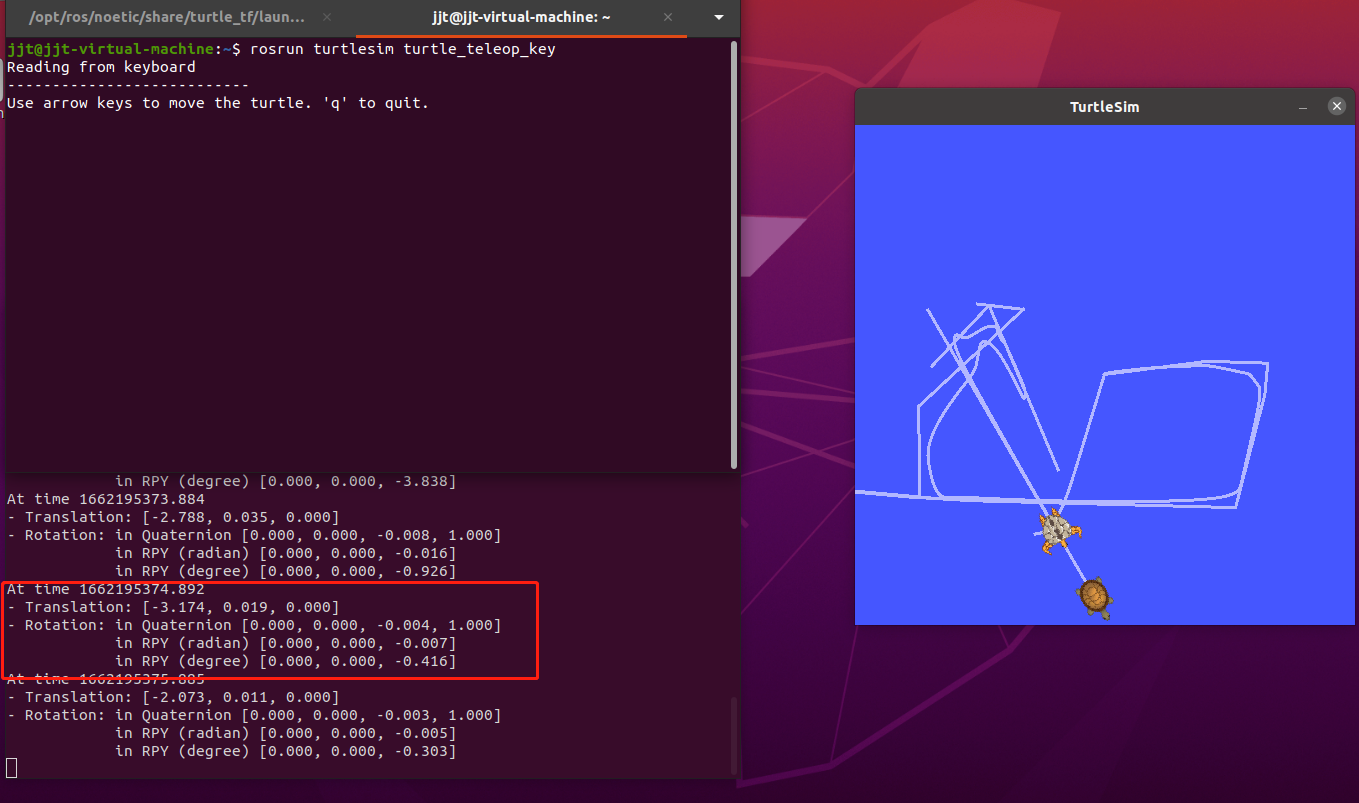
这里包含了Translation和Rotation的信息。
Translation表示了相对位移的信息（是一个3×1的向量）。
Rotation表示了旋转矩阵的信息（一个3×3的矩阵，但自由度为3），它又有两种表示方式：
1.RPY表示法(pitch俯仰角、yaw偏航角、roll翻滚角)
2.四元数法(Quaternion)
都可以表示旋转矩阵的信息，这些概念理解建议学习前面提到的机器人运动学基础。

Rotation和Translation合起来可以构成变换矩阵(4×4，见本节第一部分的图)。
我这里再放一幅Rotation和Translation包含所有的变换信息的图方便理解。

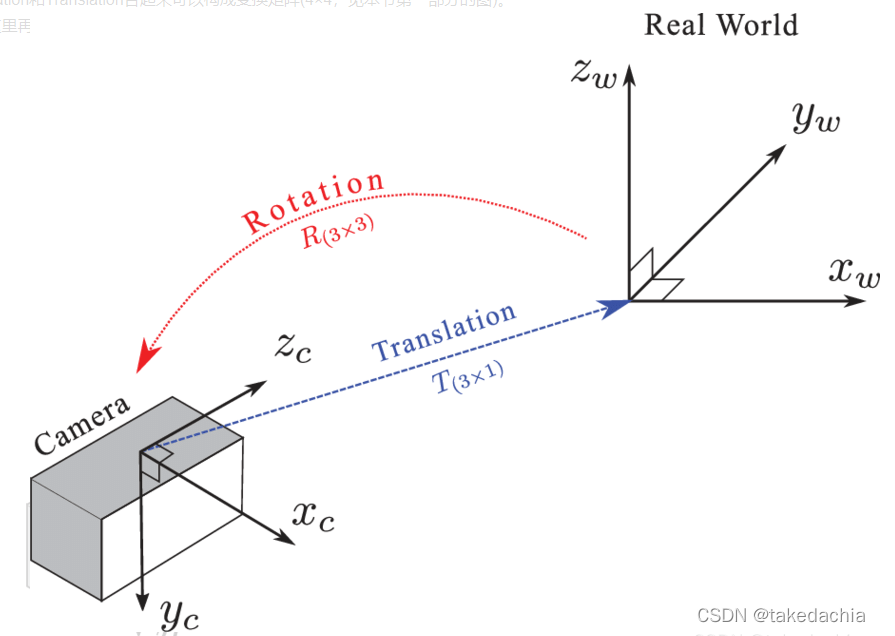
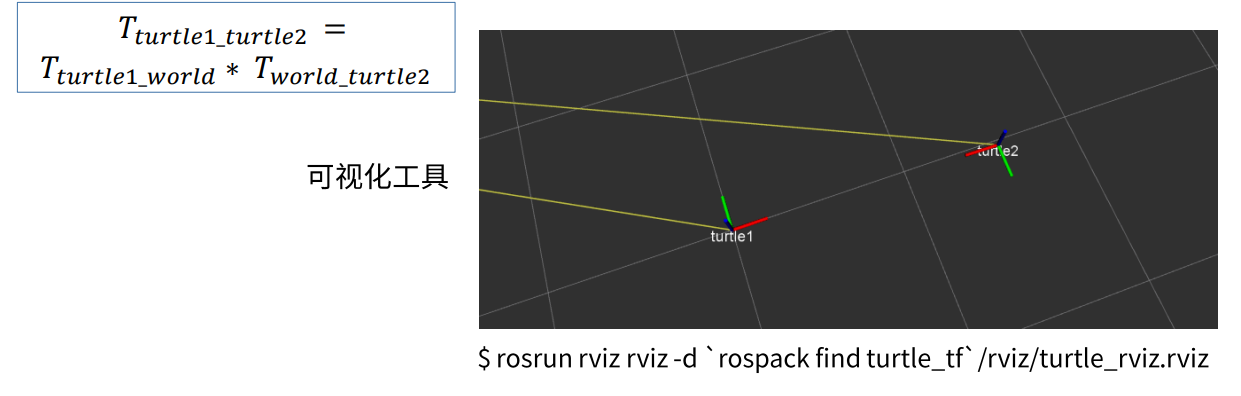
坐标相对位置关系可视化2（rviz）

rviz工具会在后面详述，先体验一下，输入：

rosrun rviz rviz -d `rospack find turtle_tf` /rviz/turtle_rviz.rviz

打开rviz界面。
上面Fixed Frame选 world。Add选添加TF，可以看到3个坐标系了。

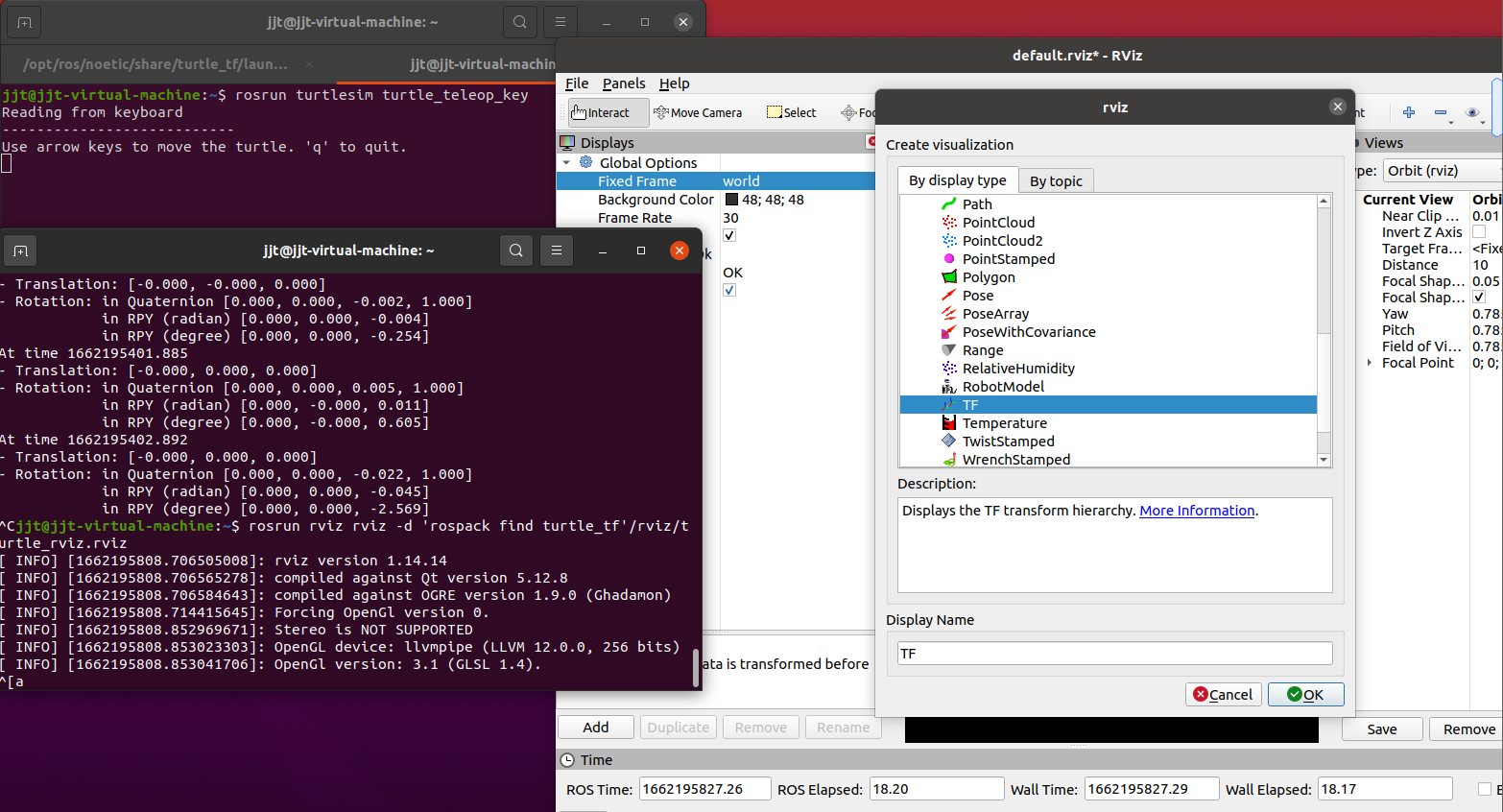
控制海龟运动，坐标系发生改变，然后坐标系turtle2原点会靠近turtle1原点

下图中左边变换矩阵的运算，其实就是坐标移动的本质。两个坐标系相对于world坐标系的变换的乘积可以求得两个坐标系相对的变换关系。