省选补题记录
省选补题记录
把 \(15-20\) 年的省选题挨个写了写。
省选联考2020
DAY1T1 冰火战士
题意描述
有两种战士,冰系战士和火系战士,每个战士有两个参数温度和能量。
对于冰系战士,如果赛场温度不低于其自身温度,那么它可以出战。
对于火系战士,如果赛场温度不高于其自身温度,那么它可以出战。
对于每一个赛场温度,冰火双方消耗的能量总和为 \(\min \{\text{能够参赛冰系战士的能量之和},\text{能够参赛的火系战士的能量之和}\} \times 2\) 。
现在想让你找一个最佳赛场温度使得冰火双方消耗的能量总和最大。
有 \(q\) 次操作,每次操作分两种,新来一个温度为 \(x\), 能量为 \(y\) 的冰系/火系战士,删除第 \(k\) 次操作。
每次操作之后,问你最佳赛场温度和冰火双方消耗的能量总和为多少。
数据范围:\(1\leq q\leq \times 2\times 10^6,x_i\leq 2\times 10^9,\sum y_i\leq 10^9\) 。
solution
树状数组/线段树+二分+卡常 。
我们先把所有的战士按温度从小到大排序。
不难发现有这样几个条件:
- 冰系战士能出战的是一段前缀。
- 火系战士能出战的是一段后缀。
- 最佳赛场温度一定是某位战士的温度。
我们设 \(fire(i)\) 表示火系战士能量的后缀和,\(ice(i)\) 表示冰系战士能量的前缀和。
然后我们把 \(fire(i),ice(i)\) 关于时间 \(i\) 的函数画一下:
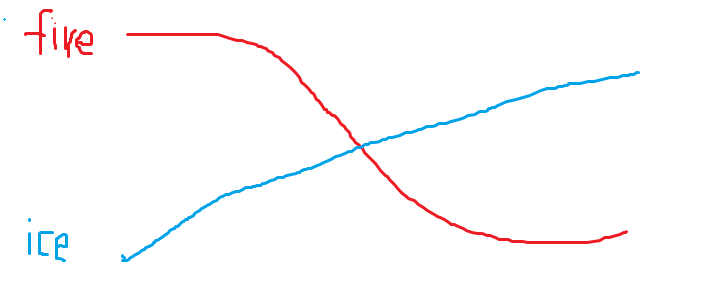
这里由于温度是整数,所以函数图像不一定是连续的,这里为了好看点就化成连续的了。
那么 \(\min(fire(i),ice(i))\) 的函数图像就是下面的那一部分。
不难发现两个函数图像的交点处的 \(\min(fire(i),ice(i))\) 的取值是最大的。
但由于其函数图像不连续,所以我们取最靠近交点的两个地方,即:
- 最大的满足 \(fire(i) > ice(i)\) 的 \(i\)。
- 最小的满足 \(ice(i)>fire(i)\) 的 \(i\) 。
然后由于 \(fire(i)\) 单调递减,\(ice(i)\) 单调递增,所以二分一下即可。
由于每次加入/删除一个战士都要维护一下前/后缀和,随便拿树状数组一下就好了。
复杂度:\(O(n\log ^2 n)\) 。
好像还有 \(O(nlogn)\) 的在树状数组上二分的做法,但我没看懂,所以就咕咕咕了。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
#include<queue>
using namespace std;
const int N = 2e6+10;
int n,fire,ice,cnt,inf,ans,pos;
int b[N],t1[N],t2[N];
struct node
{
int opt,type,x,y;
}q[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
int lowbit(int x){return x & (-x);}
void chenge(int x,int w)
{
for(; x; x -= lowbit(x)) t1[x] += w;
}
void modify(int x,int w)
{
for(; x <= inf; x += lowbit(x)) t2[x] += w;
}
int ask1(int x)//火
{
int res = 0;
for(; x <= inf; x += lowbit(x)) res += t1[x];
return res;
}
int ask2(int x)//冰
{
int res = 0;
for(; x; x -= lowbit(x)) res += t2[x];
return res;
}
void Erfen()
{
int L = 1, R = inf, ans1 = 0, p1 = 0;
while(L <= R)
{
int mid = (L + R)>>1;
int res1 = ask1(mid), res2 = ask2(mid);
if(res1 >= res2)
{
p1 = mid;
ans1 = res2;
L = mid + 1;
}
else R = mid - 1;
}
int ans2 = min(ask1(p1+1),ask2(p1+1)), p2;
L = p1+1, R = inf;
while(L <= R)
{
int mid = (L + R)>>1;
int res1 = ask1(mid), res2 = ask2(mid);
if(min(res1,res2) == ans2)
{
p2 = mid;
L = mid + 1;
}
else R = mid - 1;
}
if(ans1 == ans2) ans = ans1, pos = max(p1,p2);
else if(ans2 > ans1) ans = ans2, pos = p2;
else ans = ans1, pos = p1;
if(ans*2 == 0) printf("Peace\n");
else printf("%d %d\n",b[pos],ans*2);
}
int main()
{
// freopen("a.in","r",stdin);
// freopen("a.out","w",stdout);
n = read();
for(int i = 1; i <= n; i++)
{
q[i].opt = read();
if(q[i].opt == 1)
{
q[i].type = read();
q[i].x = read();
q[i].y = read();
b[++cnt] = q[i].x;
}
else q[i].x = read();
}
sort(b+1,b+cnt+1);
inf = unique(b+1,b+cnt+1)-b-1;
for(int i = 1; i <= n; i++) if(q[i].opt == 1) q[i].x = lower_bound(b+1,b+inf+1,q[i].x)-b;
for(int i = 1; i <= n; i++)
{
if(q[i].opt == 1)
{
if(q[i].type == 1)
{
fire++;
chenge(q[i].x,q[i].y);
}
else
{
ice++;
modify(q[i].x,q[i].y);
}
}
else
{
int id = q[i].x;
if(q[id].type == 1)
{
fire--;
chenge(q[id].x,-q[id].y);
}
else
{
ice--;
modify(q[id].x,-q[id].y);
}
}
if(!fire || !ice) printf("Peace\n");
else Erfen();
}
fclose(stdin); fclose(stdout);
return 0;
}
DAY1T2 组合数问题
题意描述
求 \(\left(\displaystyle\sum_{k=0}^{n}f(k)\times x^k\times {n\choose k}\right) \bmod p\)
其中 \(f(k)\) 为一个给定的 \(m\) 次多项式 \(f(k) = a_0k^0+a_1k^1+...+a_mk^m\) 。
数据范围:\(n\leq 10^9,m\leq 1000\) 。
solution
数论数学+斯特林数。
我们要求的其实是:\(\displaystyle\sum_{k=0}^{n} \sum_{j=0}^{m} a^jk^j\times x^k\times {n\choose k}\)
后面有关于组合数的一项,所以我们考虑把多项式转化为下降幂多项式。
推一下转化的柿子:
根据 \(m^n = \displaystyle\sum_{i=0}^{n} \begin{Bmatrix}n\\i\end{Bmatrix}m^{\underline i}\), 则有:
\(\displaystyle\sum_{i=0}^{n} a_ix^i=\displaystyle\sum_{i=0}^{n} a^i\sum_{j=0}^{i} \begin{Bmatrix}i\\j\end{Bmatrix} x^{\underline j}\)
交换一下求和顺序可得:
\(\displaystyle\sum_{i=0}^{n}a_ix^i = \sum_{i=0}^{n}x^{\underline i} \sum_{j=i}^{n} \begin{Bmatrix}i\\j\end{Bmatrix}a^j\)
设 \(\displaystyle b_i = \sum_{j=i}^{n}\begin{Bmatrix}i\\j\end{Bmatrix} a_j\) ,那么 \(\displaystyle\sum_{i=0}^{n} a_ix^i = \sum_{i=0}^{n}b_ix^{\underline i}\)。
把这个代入原式可得:
\(\displaystyle\sum_{k=0}^{n} \sum_{j=0}^{m} a_jk^j\times x^k\times {n\choose k}\)
\(=\displaystyle\sum_{k=0}^{n}\sum_{j=0}^{m}b_jk^{\underline j}\times x^k\times {n\choose k}\)
交换一下求和顺序可得:
\(原式=\displaystyle\sum_{j=0}^{m} b_j\sum_{k=0}^{n} k^{\underline j}\times x^k\times {n\choose k}\)
关于组合数和下降幂有一个很好的性质:
\(\displaystyle k^{\underline m} \times {n\choose k} = {n-m\choose k-m}\times n^{\underline m}\)
具体证明如下:
\(\displaystyle k^{\underline m}\times {n\choose k} = {k!\over (k-m)!}\times {n!\over k!(n-k)!} = {n!\over (k-m)! (n-k)!} = {{n!(n-m)!}\over (k-m)!(n-k)!(n-m)!} = {n!\over (n-m)!} {(n-m)!\over (k-m)!(n-k)!} = n^{\underline m}\times {n-m\choose k-m}\)
把这个带回去可得:
\(原式=\displaystyle\sum_{j=0}^{m} b_jn^{\underline j}\sum_{k=0}^{n} x^k\times {n-j\choose k-j}\)
又因为当 \(k>j\) 的时候,\({n-j\choose k-j} = 0\), 所以第二层循环只需要枚举到 \(j\) 就可以了,即:
\(原式=\displaystyle\sum_{j=0}^{m} b_j n^{\underline j} \sum_{k=0}^{j} x^k\times {n-j\choose k-j}\)
根据二项式定理可得:\({n-j\choose k-j}\times x^k \times 1^{k-j} = (1+x)^{n-j}\)
带回去可得:
\(原式=\displaystyle\sum_{j=0}^{m} b_jn^{\underline j}(1+x)^{n-j}\)
然后 \(O(m^2)\) 直接算即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int N = 5010;
int n,x,p,m,ans;
int jz[N],s[N][N],a[N],b[N];
inline int read()
{
int s = 0, w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
int ksm(int a,int b)
{
int res = 1;
for(; b; b >>= 1)
{
if(b & 1) res = res * a % p;
a = a * a % p;
}
return res;
}
signed main()
{
n = read(); x = read(); p = read(); m = read();
for(int i = 0; i <= m; i++) a[i] = read();
s[0][0] = jz[0] = 1;
for(int i = 1; i <= m; i++) jz[i] = jz[i-1] * i % p;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= m; j++)
{
s[i][j] = (s[i-1][j-1] + j * s[i-1][j] % p) % p;
}
}
for(int i = 0; i <= m; i++)
{
for(int j = i; j <= m; j++)
{
b[i] = (b[i] + s[j][i] * a[j] % p) % p;
}
}
int w = 1;
for(int i = 0; i <= m; i++)
{
int tmp = ksm(x+1,n-i);
ans = (ans + b[i] * w % p * tmp % p * ksm(x,i) % p) % p;
w = w * (n-i) % p;
}
printf("%lld\n",ans);
return 0;
}
DAY1T3 魔法商店
论文题,不会写,咕咕咕。
DAY2T1 信号传递
题意描述
给你一个长度为 \(n\) 的序列 \(s\), \(s_i\) 和 \(s_{i+1}\) 之间有三种传递方式:
- \(s_{i+1}\) 在 \(s_{i}\) 的右边,花费为 \(p_{s_{i+1}}-p_{s_{i}}\)
- \(s_{i+1}\) 在 \(s_i\) 的左边,花费为 \(k\times (p_{s_{i+1}}+s_{i})\)
- \(s_{i+1}=s_i\) 则花费为 \(0\)
其中 \(p\) 是一个大小为 \(m\) 的排列,\(p_i\) 表示 \(i\) 在排列 \(p\) 中的位置。
现在让你确定一个排列 \(P\), 使得传递的花费最少。
数据范围:\(n\leq 10^5,m\leq 23\) 。
solution
毒瘤卡常状压题。
有一个很显然的状压 \(dp\) 的想法就是设 \(f[s]\) 表示已经确定了前 \(|s|\) 个位置上的数,且这些位置上的数的集合为 \(s\)。
其中 \(s\) 是一个 \(0/1\) 串,\(|s|\) 表示 \(s\) 中 \(1\) 的个数,若 \(s\) 的第 \(i\) 位为 \(1\) 则表示第 \(i+1\) 个数的位置已经被确定了,为 \(0\) 则相反) 。
设 \(t[i][j]\) 表示 \(s_k\) 为 \(i\) 且 \(s_{k+1}\) 为 \(j\) 的次数。这个在输入的时候就可以预处理出来。
转移则有:\(\displaystyle f[s\text{^} (1<<(i-1))] = \min(f[s] + (|s|+1)\times \sum_{j\in s} (k*t[i][j]+t[j][i])) + (|s|+1)\times \sum_{j\notin s} (k*t[j][i]+t[i][j])\)
解释一下:我们枚举第 \(|s|+1\) 位置上的数,设其为 \(i\), 那么 \(j\in s\) 则表示 \(j\) 在 \(i\) 的左边,反之 \(j\notin s\) 则 \(j\) 在 \(i\) 的右边。分情况讨论一下传递的代价:
- \(j\) 在 \(i\) 的左边,传递方向为 \(i\rightarrow j\), 则代价为 \((|s|+1)\times k\times t[i][j]\)
- \(j\) 在 \(i\) 的左边,传递方向为 \(j\rightarrow i\), 则代价为 \((|s|+1)\times t[j][i]\)
- \(j\) 在 \(i\) 的右边,传递方向为 \(i\rightarrow j\) ,则代价为 \((|s|+1)\times t[i][j]\)
- \(j\) 在 \(i\) 的右边,传递方向为 \(j-i\), 则代价为 \((|s|+1)\times k\times t[j][i]\)
我们从小到大枚举 \(s\), 就可以做到 \(O(m^22^m)\) 的时间复杂度,空间复杂度则为 \(O(m2^m)\) 。
然后我做到这里就不太会了,看了看题解才过了这道题。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
#include<queue>
using namespace std;
const int N = 1<<23;
int n,m,K,x,last;
int f[N],t[24][24];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
int main()
{
n = read(); m = read(); K = read();
for(int i = 1; i <= n; i++)
{
x = read();
if(i > 1) t[last][x]++;
last = x;
}
memset(f,127,sizeof(f));
f[0] = 0;
for(int i = 0; i < (1<<m); i++)
{
int cnt = 0;
for(int j = 1; j <= m; j++) if((i>>(j-1))&1) cnt++;
for(int j = 1; j <= m; j++)
{
if(!((i>>(j-1))&1))
{
int sum = 0;
for(int k = 1; k <= m; k++)
{
if((i>>(k-1))&1) sum += K*t[j][k], sum += t[k][j];
else if(j != k) sum += K*t[k][j], sum -= t[j][k];
}
f[i^(1<<(j-1))] = min(f[i^(1<<(j-1))],f[i]+sum*(cnt+1));
}
}
}
printf("%d\n",f[(1<<m)-1]);
return 0;
}
考虑继续卡常优化一下。
设 \(cost(s,i)\) 为 \(\sum_{j\in s} (k*t[i][j]+t[j][i])) + \sum_{j\notin s} (k*t[j][i]+t[i][j])\) ,也就是 \(|s|+1\) 前的系数。
处理完这个 \(cost(s,i)\) 那么我们在转移 \(f\) 的时候复杂度就降为了 \(O(m2^m)\) 。
预处理 \(cost(s,i)\) 其实是可以 \(O(m2^m)\) 的做的。具体来说就是:
\(\displaystyle cost(0,i) = \sum_{j\neq i} k\times t[j][i] + t[i][j]\)
\(cost(s,i) = cost(s-(1<<(j-1),i) + t[i][j]\times (1+k) + t[j][i]\times (1-k)\) (其中 \(s\) 的第 \(j-1\) 位为 \(1\))。
解释一下: 对于 \(cost(0,i)\) 这时候 \(j(j\neq i)\) 都在 \(i\) 的右边,所以传递代价为 \(k\times t[j][i]+t[i][j]\) 。
由 \(s-(1<<(j-1))\) 到 \(s\) 相当于是 \(j\) 原来在 \(i\) 的右边,现在到了左边的位置,我们只需要把 \(j\) 在 \(i\) 的右边的代价减去,在加上 \(j\) 在 \(i\) 的左边的传递代价, 即 \(t[i][j]\times (1+k) + t[j][i]\times (1-k)\) ,然后我们就可以由 \(cost(s-(1<<(j-1)),i)\) 算出 \(cost(s,i)\) 。
因为每次都是由 \(s\) 减去一个数转移过来的,所以可以每次减去 \(lowbit(s)\) 转移。
那么递推 \(cost(s,i)\) 的复杂度就变为了 \(O(m2^m)\) 。
写完交上去之后,你会发现 \(\text{MLE}\) 了,毒瘤出题人卡了一手空间。
至于如何卡过去,可以看这篇 题解 。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
#include<queue>
using namespace std;
const int N = 1<<23;
int n,m,K,x,last;
int t[24][24],lg[N],num[N],f[N],cost[N/2][24];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
int lowbit(int x){return x & (-x);}
int main()
{
n = read(); m = read(); K = read();
for(int i = 1; i <= n; i++)
{
x = read()-1;
if(i > 1) t[last][x]++;
last = x;
}
lg[0] = -1; num[0] = 0;
for(int i = 1; i < (1<<m); i++)
{
lg[i] = lg[i>>1] + 1;
num[i] = num[i>>1] + (i&1);
}
for(int i = 0; i < m; i++)
{
for(int j = 0; j < m; j++)
{
if(i != j) cost[0][i] += K * t[j][i] - t[i][j];
}
for(int j = 1; j < (1<<(m-1)); j++)
{
int k = lowbit(j), o = lg[k];
if(o >= i) o++;
cost[j][i] = cost[j^k][i] + t[i][o] * (1+K) + t[o][i] * (1-K);
}
}
memset(f,127,sizeof(f));
f[0] = 0;
for(int i = 1; i < (1<<m); i++)
{
for(int j = i, y; y = lowbit(j); j ^= y)
{
int o = lg[y], s = i^y;
f[i] = min(f[i],f[i^y]+num[i]*cost[s&y-1|s>>o+1<<o][o]);
}
}
printf("%d\n",f[(1<<m)-1]);
return 0;
}
DAY2T2 树
题意描述
给你一棵有根树,定义 \(x\) 节点的价值为 \(x\) 的子树中每个节点的点权加上到 \(x\) 的距离的异或和。
即:\(val(x)=(v_{c1}+d(c_1,x))⊕(v_{c2}+d(c_2,x))⊕⋯⊕(v_{c_k}+d(c_k,x))\)
让你求 \(\displaystyle\sum_{i=1}^{n} val(i)\) 。
数据范围:\(1\leq n,v_i\leq 525010\) 。
solution
\(\text{tire}\) 树/其他做法。
对于这题,考虑怎么拿 \(tire\) 树来维护。
我们对于每一个节点维护一个 \(\text{tire}\) 树,\(\text{tire}\) 树里面存其子树中每个节点的点权加上到 \(x\) 的距离。
暴力插数显然是过不去的,考虑继续优化。
不难发现这样一个性质:对于 \(u\) 的 \(\text{tire}\) 树中的每一个二进制数 \(+1\),恰好就是 \(fa(u)\) \(\text{tire}\) 树中的数的一部分(这个可以根据 \(val(u)\) 的计算式推出来)。
然后我们就要维护一下三种操作:
- 向 \(\text{tire}\) 树中插入一个数。
- 把 \(u\) 和 \(fa(u)\) 的 \(\text{tire}\) 树合并。
- 把 \(u\) 的 \(\text{tire}\) 树中的二进制数 \(+1\) 。
- 查询当前 \(\text{tire}\) 树中所有数的异或和。
操作1是 \(\text{tire}\) 树的常规操作,这里就不说了。
操作2的话,\(\text{tire}\) 树的合并其实和线段树合并是类似的,把 \(\text{tire}\) 树看成一棵线段树,直接合并即可。
这两个的不同点在于线段树的节点维护的是区间的信息,但 \(\text{tire}\) 树的节点维护的每一位的信息。
但合并的实质都是把两个节点维护的信息合并。
void merage(int &x,int y,int wei)
{
if(!x){x = y; return;}
if(!y) return;
siz[x] += siz[y];
merage(tr[x][0],tr[y][0],wei+1);
merage(tr[x][1],tr[y][1],wei+1);
up(x,wei);
}
对于操作3,我们考虑对于一个二进制数,加1之后会变成什么样,举几个例子:
01111 -> 11111
11011 -> 00111
10011 -> 01011
不难发现如果最低位为 \(0\) ,那么 \(+1\) 之后这一位就变为了 \(1\), 对于最低位为 \(1\) 的数,\(+1\) 之后这一位变为了 \(0\), 同时下一位进 \(1\) (相当于下一位+1)。
在 \(\text{tire}\) 树上,我们考虑从低位到高位建 \(\text{tire}\) 树,+1操作就把当前节点的 \(\text{tr[x][0]}\) 和 \(\text{tire[x][1]}\) 交换一下(+1之后,\(0\) 变为了 \(1\),\(1\) 变为了 \(0\)),在递归处理 \(\text{tr[x][0]}\) (处理进位操作)。
代码也很好写:
void Jinwei(int x,int wei)//+1操作
{
if(!x) return;
swap(tr[x][0],tr[x][1]);
Jinwei(tr[x][0],wei+1);
up(x,wei);
}
对于操作4,一开始我想的是维护每一位 \(1\) 的个数,但+1操作的时候需要遍历整颗 \(\text{tire}\) 树,然后就挂掉了。
但实际上我们只需要对 \(\text{tire}\) 树的节点维护其子树中数的异或和即可(具体怎么维护可以看代码)。
解决完这四个操作之后,我们这道题就做完了。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
#include<queue>
using namespace std;
#define LL long long
const int N = 550000;
const int M = 5e7+10;
int n,m,tot,cnt,x;
int head[N],w[N],rt[N],siz[M],tr[M][2],sum[M];
LL ans;
struct node
{
int to,net;
}e[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
void add(int x,int y)
{
e[++tot].to = y;
e[tot].net = head[x];
head[x] = tot;
}
void up(int o,int wei)
{
////假设o维护的是第i位的信息,那么sum[o]表示o的子树中所有的数的只看 i~23 位,其他位忽略为0的异或和
sum[o] = sum[tr[o][0]] ^ sum[tr[o][1]];//首先sum[o] 一部分为其左儿子和右儿子的异或和,另一部分为这一位为1的数的贡献
if(siz[tr[o][1]]&1) sum[o] += 1<<wei;//如果这一位为1的数有奇数个那么异或起来这一位为1否则为0
}
void insert(int p,int x,int wei)//插入一个数
{
if(wei > 23) return;
siz[p]++;
int c = (x>>wei)&1;
if(!tr[p][c]) tr[p][c] = ++cnt;
insert(tr[p][c],x,wei+1);
up(p,wei);
}
void merage(int &x,int y,int wei)//tire树合并
{
if(!x){x = y; return;}
if(!y) return;
siz[x] += siz[y];
merage(tr[x][0],tr[y][0],wei+1);
merage(tr[x][1],tr[y][1],wei+1);
up(x,wei);
}
void Jinwei(int x,int wei)//+1操作
{
if(!x) return;
swap(tr[x][0],tr[x][1]);
Jinwei(tr[x][0],wei+1);
up(x,wei);
}
void dfs(int x,int fa)
{
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa) continue;
dfs(to,x);
merage(rt[x],rt[to],0);
}
Jinwei(rt[x],0);
insert(x,w[x],0);
ans += sum[rt[x]];
}
int main()
{
n = read(); cnt = n;
for(int i = 1; i <= n; i++) w[i] = read();
for(int i = 2; i <= n; i++) x = read(), add(x,i);
for(int i = 1; i <= n; i++) rt[i] = i;
dfs(1,0);
printf("%lld\n",ans);
return 0;
}
DAY2T3 作业题
不会矩阵树。



