省选模拟测试17

\(T1\) 不会轮廓线 \(dp\)，呜呜呜。

\(T2\) 想到了要把环单独处理一下，但做法是 \(O(环的大小^2)\) 的，担心被卡就没写。

\(T3\) 往容斥和二项式反演方面去想，想了半天没想出来。

T1 Gird

题目内容

你有一个 \(n\) 行 \(m\) 列的教室，其中某些位置不能坐人。

你的班上有 \(k\) 对 CP，你对八卦早已失去了兴趣，转而想要知道有多少种给这 \(2k\) 位同学排座位的方式，使得每对 CP 的座位不相邻（有些位置可能会空出来，方案不同当且仅当某个位置状态不同，即坐着不同的同学）。

结果对 \(10^9+7\) 取模。

数据范围：\(nm\leq 144\)

solution

首先注意到 \(nm\leq 144\) ，那么就意味着 \(\min(n,m)\leq 12\) ，然后我们就可以状压 \(dp\) 了。

设 \(f(pos,S,x)\) 表示做到 \(pos\) 位置，最近这 \(m\) 个位置的状态是 \(S\),已经有 \(x\) 对的方案数。

在反演一下就可以得到答案，巴拉巴拉。。。

T2 cactus

题目内容

你有一棵仙人掌，你想要知道所有点两两最短路之和，即，\(\sum\limits_{i<j} dis(i,j)\)。

仙人掌是一张无向简单连通图，无重边自环，且每条边属于至多一个简单环。

本题中边没有权值，即可以认为边权均为 \(1\)。

数据范围：\(n\leq 3\times 10^5,m\leq 6\times 10^5\)

solution

这道题正解思路挺好想的，但是怎么处理比较关键。\(O(环的大小^2)\) 的做法好像被出题人点名卡了。

首先我们可以对整棵树求一个 \(DFS\) 树，然后对于环上的边和树边单独考虑。

首先对于树边的情况，对答案的贡献显然为：\(siz[x]\times (n-siz[x])\)

然后考虑怎么处理环的情况，我们把整张图画出来，他长成这个样子：

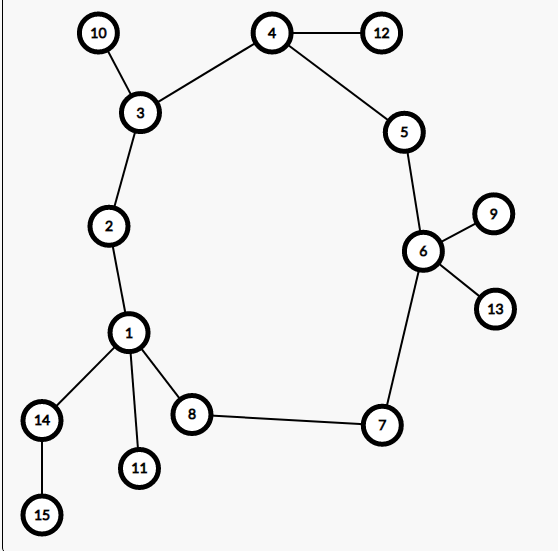
也就是环上每个点下面都挂着若干个点组成的子树，设这个子树大小为 \(f[i]\) 。

不难发现两个点对答案的贡献为：\(f[i]\times f[j]\times \min(j-i,n-(j-i))\)

考虑两点之间的路径被经过多少次，就可以得出来上面的那个柿子了。

然后我们的问题就变成可怎么在 \(O(n)\) 的时间内求出环上两个点之间的贡献。

有一个 \(n\log n\) 的 \(FFT\) 做法，我不太会写，就被咕掉了。

假设我们现在枚举到了 \(i\) 点，然后我们要算 \(\displaystyle \sum_{j>i} f[i]\times f[j]\times \min(j-i,n-(j-i))\)

对于后面的那个取 \(\min\) 就是两点之间的距离，考虑求一个 \(k\) 使得 \(i+1- k\) 的点到 \(i\) 点的距离为 \(j-i\),

而 \(k+1,n\) 的点到 \(i\) 点的距离为 \(n-(j-i)\) 。

然后我们把两个柿子拆一下变为：

\(\displaystyle \sum_{j=i+1}^{k} f[i]\times f[j]\times (j-i) = \displaystyle f[i]\times \left( \sum_{j=i+1}^{k} f[j]\times j- f[j]\times i \right) = f[i] \times \left(\sum_{j=i+1}^{k} f[j]\times [j] - i\times \sum_{j=i+1}^{k} f[j]\right)\)

\(\displaystyle\sum_{j=k+1}^{n} f[i]\times f[j]\times(n-j+i) = f[i]\times\left(\sum_{j=k+1}^{n} f[j]\times (n+i)-f[j]\times j\right) = f[i]\times \left(\left(n+i\right)\times \sum_{j=k+1}^{n} f[j] - \sum_{j=k+1}^{n} f[j]\times j \right)\)

然后你就会发现，只需要维护一下 \(f[i]\) 以及 \(f[i]\times i\) 的一个前缀和就好了。

复杂度：\(O(n+m)\)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
#define int long long
#define mp make_pair
const int N = 3e5+10;
int n,m,u,v,tot,ans,num,cnt,top;
int head[N],dfn[N],sum1[N],sum2[N],siz[N],sta[N],fa[N];
pair<int,int> p[N<<1];
bool vis[N];
struct node
{
	int to,net;
}e[N<<2];
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s * w;
}
void add(int x,int y)
{
	e[++tot].to = y;
	e[tot].net = head[x];
	head[x] = tot;
}
void dfs(int x,int ff)
{
	dfn[x] = ++num; siz[x] = 1; fa[x] = ff;
	for(int i = head[x]; i; i = e[i].net)
	{
		int to = e[i].to;
		if(!dfn[to]) 
		{
			dfs(to,x);
			siz[x] += siz[to];
		}
		else if(to != ff && dfn[to] < dfn[x]) p[++cnt] = mp(x,to);
	}
}
signed main()
{
//	freopen("cactus.in","r",stdin);
//	freopen("cactus.out","w",stdout);
	n = read(); m = read();
	for(int i = 1; i <= m; i++)
	{
		u = read(); v= read();
		add(u,v); add(v,u);
	}
	dfs(1,0);
	for(int i = 1; i <= cnt; i++)
	{
		int x = p[i].first, to = p[i].second, siz_son = 0; top = 0;
		for(; x != to; x = fa[x])
		{
			sta[++top] = siz[x]-siz_son;
			siz_son = siz[x]; vis[x] = 1;
		}
		sta[++top] = n-siz_son;
		for(int i = 1; i <= top; i++) sum1[i] = sum1[i-1] + sta[i], sum2[i] = sum2[i-1] + sta[i] * i;
		for(int i = 1; i <= top; i++)
		{
			int j = min(top,i+top/2);
			ans += sta[i] * (sum2[j]-sum2[i] - (sum1[j]-sum1[i])*i);//i+1...j
			ans += sta[i] * ((sum1[top]-sum1[j])*(top+i) - (sum2[top]-sum2[j]));//j+1...n
		}
	}
	for(int i = 1; i <= n; i++) if(!vis[i]) ans += siz[i] * (n-siz[i]);
	printf("%lld\n",ans);
	fclose(stdin); fclose(stdout);
	return 0;
}

T3 color

题目内容

你有一个 \(2\) 行 \(n\) 列的网格，你要给每个格子染上三种颜色（红绿蓝）之一。

你还提了很多要求：任意两个相邻格子颜色不能相同；任何一个 \(2\times 2\) 的块里，每种颜色都必须出现过。

现在你还想求出，恰好分别染了 \(R,G,B\) 个红、绿、蓝格子的方案数，结果对 \(10^9+7\) 取模。

数据范围：\(n\leq 5\times 10^5,R,G,B\leq 2\times n, R+G+B = 2n\)

solution

组合计数。

首先我们构造一个序列 \(a[i]\) 表示第 \(i\) 列没有出现过的颜色。

设红绿蓝在序列 \(a\) 中出现次数为 \(r,g,b\)， 这个根据 \(R,G,B\) 很容易就可以求出来。

不难发现题目中的条件等价于序列 \(a[i]\) 中相邻的两个不同且红绿蓝格子恰好出现 \(r,g,b\) 次。

然后我们就可以组合计数了。

首先考虑把红色分为 \(i\) 组，方案数显然为 \({r-1}\choose i-1\) ,如图：

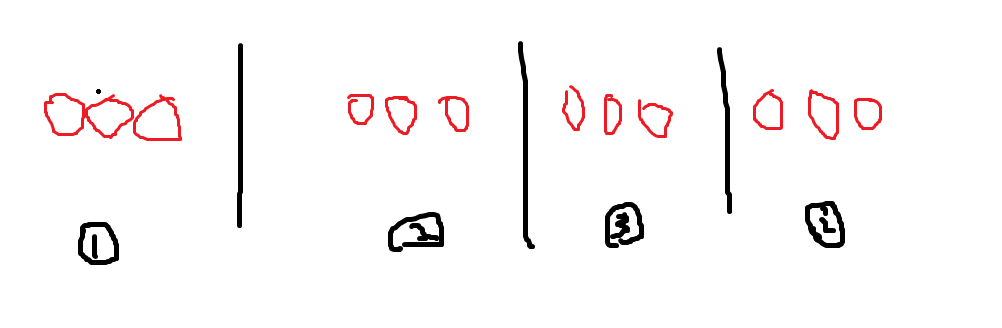
接着我们考虑把绿色格子往每组之间的空隙中插，显然绿色格子的组数只能有 \(i-1,i,i+1\) 三种取值。

枚举 \(j\in{\{i-1,i,i+1\}}\) ，那么方案数为 \({g-1\choose j-1}\) 。

注意当 \(j=i\) 的时候，我们此刻既可以往前面放又可以往后面放，所以方案数还有乘上 \(2\) 。

处理完上面两步后，情况就变为了：

不难发现相连的两个颜色相同的位置有 \(r-i+g-j\) 个，显然我们肯定是要往这些位置都放上一个蓝色小球的。

那么剩下的 \(b-(r-i+g-j)\) 个蓝色只能放在相邻的两个颜色不同的地方，显然这样的位置有 \(i+j-1\) 个。

所以方案数为 \({b-(r-i+g-j)}\choose i+j-1\) 。

这样我们就考虑到所有的情况了。

计算式：\(\displaystyle \sum_{i=1}^{r}\sum_{j\in\{i-1,i,i+1\}} (1+[i=j]) \times {{r-1}\choose i-1}\times {{g-1}\choose j-1} \times {{b-(r-i+g-j)}\choose i+j-1}\) 。

直接 \(O(n)\) 算即可。

注意：在计算组合数的时候，可能会出现 \(m<0\) 或者 \(n<m\) 的情况，这时候特判一下就好了。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int p = 1e9+7;
int n,R,G,B,r,g,b,ans,jz[10000010],inv[10000010];
inline int read()
{
    int s = 0,w = 1; char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
    while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
    return s * w;
}
int ksm(int a,int b)
{
	int res = 1;
	for(; b; b >>= 1)
	{
		if(b & 1) res = res * a % p;
		a = a * a % p;
	}
	return res;
}
int C(int n,int m)
{
	if(n < 0 || m < 0 || n < m) return 0;
	return jz[n] * inv[m] % p * inv[n-m] % p;
}
signed main()
{
	n = read(); R = read(); G = read(); B = read();
	r = n-R, g = n-G, b = n-B;
	jz[0] = inv[0] = 1;
	for(int i = 1; i <= 2*n; i++) jz[i] = jz[i-1] * i % p;
	inv[2*n] = ksm(jz[2*n],p-2);
	for(int i = 2*n-1; i >= 1; i--) inv[i] = inv[i+1] * (i+1) % p;
	for(int i = 1; i <= r; i++)
	{
		for(int j = i-1; j <= i+1; j++)
		{
			ans = (ans + (1LL+(i==j)) * C(r-1,i-1) % p * C(g-1,j-1) % p * C(i+j+1,b-(r+g-i-j)) % p) % p;
		}
	}
	printf("%lld\n",ans*2%p);
	return 0;
}