省选模拟测试12
期望得分:\(50+20+30 = 100\)
实际得分:\(50+20+0 = 70\)
\(T1\) 考试的时候只打了斜率优化的部分分,稍微考虑一下估计就想出来了,可惜没时间写了。
\(T2\) 只会打爆搜的分,剩下的打了个假的贪心,也没有骗到分。
\(T3\) 看起来像是个树上问题套上了字符串,但只会打 \(O(n^2)\) 的暴力,还打挂了,难受。
T1 最大分数
题意描述
\(n\) 个数排成一排,第 \(i\) 个数为 \(T_i\) 。你可以从中标记一些数字,标记完之后,你会获得相应的分数。\(分数 = ( 所有满足 1\leq L\leq R\leq N 且区间 [l,r] 中的数全部被标记的数对 (L,R) 的个数 ) - ( 被标记的数字之和 )\)。
现在有 \(M\) 个询问,第 \(i\) 个询问有两个参数 \(P_i\) 和 \(x_i\),你需要求出把 \(T_{P_i}\) 变成 \(x_i\) 之后能够获得的分数的最大值。每组询问都是独立的。
数据范围:\(1\leq N,M\leq 3\times 10^5,1\leq T_i,x_i\leq 10^9\)
solution
斜率优化 \(dp\)
先考虑没有修改的情况我们怎么做,设 \(f[i]\) 表示前 \(i\) 个数任意选的最大的价值, \(g[i]\) 表示后 \(i\) 个数任意选的最大价值。
\(f[i]\) 和 \(g[i]\) 的转移其实是一样的,我们就拿 \(f[i]\) 举一下例子。
\(f[i]\) 转移的时候枚举极大的全被标记的区间,则有:
\(\displaystyle f[i] = \max\left(f[i-1], \max_{j=0}^{i-1}f[j-1] + {(i-j)\times (i-j+1)\over 2} - sum[i] + sum[j]\right)\)
由 \(f[i-1]\) 转移过来的时候,特判一下,后面的其实就是个斜率优化的柿子。
为了方便点,我们把所有的数都乘上 \(2\) ,最后算 \(f[i]\) 的时候在除回去即可。
我们把乘完 \(2\) 之后的柿子写好看点:
\(f[i] = f[j-1] + (i-j)^2+(i-j) - sum[i] + sum[j]\)
\(f[i] = f[j-1] + i^2+j^2-2ij + (i-j) - sum[i] + sum[j]\)
\(f[j-1]+j^2+sum[j]-j = 2ij + f[i] - i^2-i+sum[i]\)
我们要求 \(f[i]\) 的最大值,直接维护一个上凸壳即可。
\(g(i)\) 只需要倒着求一遍即可。
接下来我们考虑怎么处理带修改的情况。
实际上每个数只有选或不选两种情况,也就是我们只需要求出不选 \(P_i\) 的最大值,和选 \(P_i\) 的最大值是多少,即:
不选的情况很好考虑就是 \(f[i-1] + g[i+1]\) 。设 \(h[i]\) 表示必须选 \(i\) ,其他任意选的最大价值为多少。
则有:\(ans = \max(f[i-1]+g[i+1],h[i]-a[P_i]+x_i)\) 。
求 \(h[i]\) 可以考虑通过分治来求解,具体来说:
假设我们现在的分治区间为 \([l,r]\) ,设 \(L[i]\) 表示极大的全被标记的区间左端点为 \(i(l\leq i\leq mid)\), 右端点在 \([mid+1,r]\) 处的价值最大是多少, \(R[i]\) 表示极大的全被标记的区间右端点在 \(i(mid+1\leq i\leq r)\), 左端点在 \([l,mid]\) 处的价值最大是多少。
\(L[i]\) 和 \(R[i]\) 的转移其实是相似的,在这里我就拿 \(R[i]\) 来举例一下:
\(R[i] = \max\left(f[j-1]+ g[i+1] - sum[i] + sum[j] + {(i-j)\times (i-j+1)\over 2}\right)\)
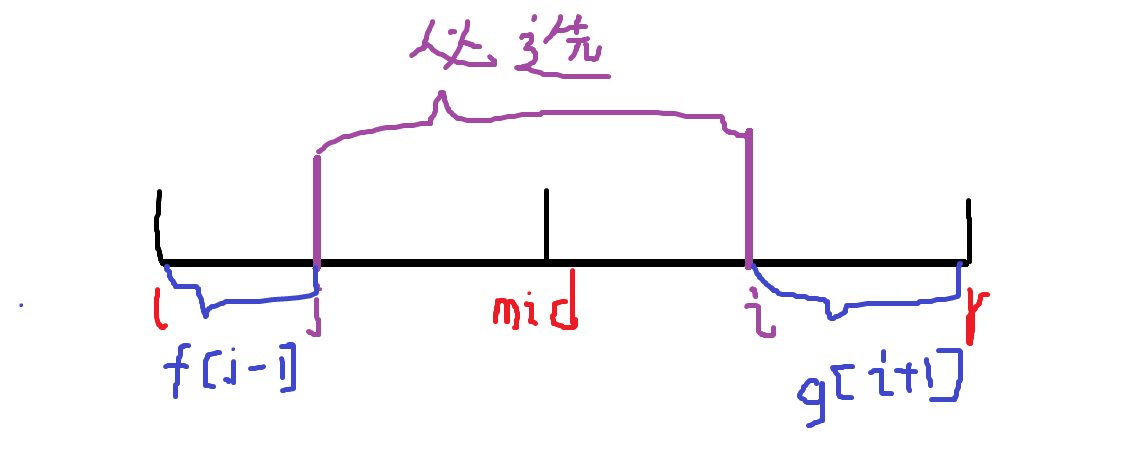
解释一下转移柿子,首先中间的 \([i,j]\) 这一段是必选的,所带来的价值为 \({(i-j)\times (i-j+1)\over 2} -sum[i]+sum[j]\) ,左右两边剩下的部分随便选最大值为 \(f[j+1]+g[i+1]\) 。
我们发现这个其实和 \(f[i]\) 的转移柿子差不多的,都是可以斜率优化的。
就是我们对 \([l,mid]\) 这一部分的点建一个上凸壳,然后在凸壳上就可以查询出 \(R[i](mid+1\leq i\leq r)\),同理对右边的点维护一个上凸壳,就可以得到 \(L[i](l\leq i\leq mid)\) 。
然后我们继续递归下去即可。
对 \(L[i]\) 求一个前缀最大值,\(R[i]\) 求一个后缀最大值,那这两个数组就可以求出 \(h[i]\)
注意:求 \(f[i],g[i]\) 的时候如果结果为负数则是可以和 \(0\) 取 \(\max\) 的,但在求 \(L[i],R[i]\) 的时候,因为一段区间是必选的,所以就不能在和 \(0\) 取 \(\max\) 了。
我们就可以在 \(O(nlogn)\) 的时间内解决本题了。
Code(写起来还是挺恶心的)
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int N = 3e5 + 5;
const int inf = 1e18;
int n,m,top,p,x,a[N],f[N],g[N],h[N],R[N],sum[N];
struct point
{
int x, y;
point(){}
point(int X,int Y) { x = X; y = Y; }
}sta[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
point operator - (const point &a, const point &b) {return point(a.x - b.x, a.y - b.y);}
int Cro(point a, point b) {return a.x * b.y - a.y * b.x;}
double slope(point a, point b)
{
return 1.0 * (b.y - a.y) / (b.x - a.x);
}
void add(int x, int y)
{
point p = point(x, y);
while(top >= 2 && Cro(sta[top]-sta[top - 1],p-sta[top - 1]) >= 0) top --;
sta[++top] = p;
}
int calc(point j,int i)
{
return j.y - i * j.x;
}
int find(int k, int opt)
{
if(!top) return 0;
int L = 2, R = top - 1, ans = 1;
while(L <= R)
{
int mid = (L + R) >> 1;
double t1 = slope(sta[mid - 1],sta[mid]), t2 = slope(sta[mid],sta[mid + 1]);
if(k <= t1 && k >= t2) {ans = mid; break;}
else if(k < t1 && k < t2) L = mid + 1;
else R = mid - 1;
}
int res = opt == 1 ? -inf : 0;
return max(max(calc(sta[1],k),calc(sta[top],k)),max(res,calc(sta[ans],k)));
}
void solve(int l, int r)
{
if(l == r) {h[l] = max(h[l],1-a[l]); return;}
int mid = (l + r) >> 1;
top = 0; int maxn = -inf;
for(int i = l;i <= mid; i++) add(i, 2 * f[i - 1] + 2ll * sum[i - 1] + i * i - 3 * i);
for(int i = mid + 1;i <= r; i++) R[i] = (find(2 * i,1) - 2 * sum[i] + 2 * g[i + 1] + i * i + 3 * i + 2) / 2;
for(int i = r; i > mid; i--)
{
maxn = max(maxn,R[i]);
h[i] = max(h[i],maxn);
}
top = 0;
for(int i = mid+1; i <= r; i++) add(i, 2 * g[i + 1] - 2 * sum[i] + i * i + 3 * i);
for(int i = l;i <= mid; i++) R[i] = (find(2 * i, 1) + 2 * sum[i - 1] + 2 * f[i - 1] + i * i - 3 * i + 2) / 2;
maxn = -inf;
for(int i = l; i <= mid; i++)
{
maxn = max(maxn,R[i]);
h[i] = max(h[i],maxn);
}
solve(l, mid);
solve(mid + 1, r);
}
signed main()
{
freopen("score.in","r",stdin);
freopen("score.out","w",stdout);
n = read();
for(int i = 1; i <= n; i++) a[i] = read();
for(int i = 1; i <= n; i++) sum[i] = sum[i - 1] + a[i];
for(int i = 1; i <= n; i++)
{
int res = find(2 * i, 0);
f[i] = max(0ll,res - 2 * sum[i] + i * i + i) / 2;
f[i] = max(f[i - 1],f[i]);
add(i,2 * f[i] + 2 * sum[i] + i * i - i);
}
reverse(a + 1, a + n + 1);
top = 0;
for(int i = 1; i <= n; i++) sum[i] = sum[i - 1] + a[i];
for(int i = 1; i <= n; i++)
{
int res = find(2 * i, 0);
g[i] = max(0ll,res - 2 * sum[i] + i * i + i) / 2;
g[i] = max(g[i - 1], g[i]);
add(i,2 * g[i] + 2 * sum[i] + i * i - i);
}
reverse(a + 1, a + n + 1);
reverse(g + 1, g + n + 1);
for(int i = 1;i <= n; i++) sum[i] = sum[i - 1] + a[i];
for(int i = 1;i <= n; i++) h[i] = -inf;
solve(1, n);
m = read();
for(int i = 1; i <= m; i++)
{
p = read(); x = read();
printf("%lld\n",max(f[p-1]+g[p+1],h[p]+a[p]-x));
}
fclose(stdin); fclose(stdout);
return 0;
}
T2 大收藏家
题意描述
小 C 是在收藏界颇负盛名的大收藏家。
这天,他带着他的藏品去参加收藏家大会,与大家交换藏品。
共有 \(n\) 名收藏家参加了这次大会,每个人都带了一种与众不同的藏品来,其中第 \(i\) 个收藏家带了 \(a_i\) 个自己类型的藏品。
因为小 C 很强,所以他是第 \(1\) 个收藏家。大会上会依次进行 \(m\) 次交换活动,每次会指定两个不同的收藏家 \(x_i,y_i\) ,这两个收藏家可以各自选择自己当前持有的一个藏品与对方交换。每次活动至多进行一次交换,可以不进行交换。
小 C 想知道,大会结束后,自己最多持有多少种不同的藏品。
数据范围:\(T\leq 10,1\leq n,m,a_i\leq 3000,1\leq x_i,y_i\leq n\)
solution
网络流。
md,他为什么要给关于树的部分分啊,这跟正解一点关系都没有。
我们要求的是最后第一个人最多有多少中物品,不妨假设第一个人除了第一件物品外,其他物品最多只能拥有一个,不难发现,这样是不会影响最后的答案的。
就相当于每个人一开始只有一件物品,剩下的 \(a_i-1\) 个位置可以用来做交换空位。
那么如果一个人一开始有一件物品,肯定会经过某种方式传到某个人手中。
然后问题就转化为了,第 \(i\) 个人有 \(1\) 件第 \(i\) 个物品,每一时刻最多有 \(a_i\) 个物品,每次操作一个人可以把一件物品传给另外一个人,问最后有多少个物品可以到第一个人手中。
不妨考虑这样建图,有源点向 \(i\) 点连一条容量为 \(1\) 的边,把每个人的每一时刻都拆成一个点 \(x_{i,j}\),由 \(x_{i,j}\) 向 \(x_{i,j+1}\) 连一条容量为 \(a_i\) 的边,如果第 \(j\) 个时刻 \(a,b\) 可以交换物品,则由 \(x_{a,j-1}\) 向 \(x_{b,j}\) 以及 \(x_{b,j-1}\) 向 \(x_{a,j}\) 连一条容量为 \(1\) 的边,最后再由 \(x_{1,m}\) 向汇点连一条容量为 \(a_1\) 的边。
这张图的最大流就是最后的答案。
不难发现我们有些边其实是不用连的,只需要由 \(x_{i,j}\) 向 \(i\) 上一次有操作的时刻连边即可。
由于最大流不超过 \(n\) ,所以复杂度为 \(O(nm)\) 的。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int inf = 1e7+10;
const int N = 1e5+10;
int T,n,m,s,t,cnt,x,y,tot = 1;
int head[N],last[N],dep[N],a[N];
struct node
{
int to,net,w;
}e[1000010];
inline int read()
{
int s = 0, w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
void add(int x,int y,int w)
{
e[++tot].to = y;
e[tot].w = w;
e[tot].net = head[x];
head[x] = tot;
}
bool bfs()
{
queue<int> q;
for(int i = 0; i <= t; i++) dep[i] = 0;
q.push(s); dep[s] = 1;
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(e[i].w && !dep[to])
{
dep[to] = dep[x] + 1;
q.push(to);
if(to == t) return 1;
}
}
}
return 0;
}
int dinic(int x,int flow)
{
if(x == t || !flow) return flow;
int rest = flow, val = 0;
for(int i = head[x]; i && rest; i = e[i].net)
{
int to = e[i].to;
if(!e[i].w || dep[to] != dep[x] + 1) continue;
val = dinic(to,min(rest,e[i].w));
if(val == 0) dep[to] = 0;
e[i].w -= val, e[i^1].w += val, rest -= val;
}
return flow - rest;
}
void slove()
{
n = read(); m = read(); s = 0; cnt = n;
for(int i = 1; i <= n; i++) a[i] = read(), last[i] = i;
for(int i = 1; i <= n; i++) add(s,i,1), add(i,s,0);
for(int i = 1; i <= m; i++)
{
x = read(); y = read();
add(cnt+1,cnt+2,1); add(cnt+2,cnt+1,0);
add(cnt+2,cnt+1,1); add(cnt+1,cnt+2,0);
add(last[x],cnt+1,a[x]); add(cnt+1,last[x],0);
add(last[y],cnt+2,a[y]); add(cnt+2,last[y],0);
last[x] = cnt+1;
last[y] = cnt+2;
cnt += 2;
}
t = cnt+1;
add(last[1],t,a[1]); add(t,last[1],0);
int flow = 0, ans = 0;
while(bfs())
{
while(flow = dinic(s,inf)) ans += flow;
}
printf("%d\n",ans);
}
void Qk()
{
cnt = 0; tot = 1;
memset(head,0,sizeof(head));
}
int main()
{
freopen("collection.in","r",stdin);
freopen("collection.out","w",stdout);
T = read();
while(T--){slove(); Qk();}
return 0;
}
T3 往事之树
题意描述
我们定义一棵往事树是一个 \(n\) 个点 \(n-1\) 条边的有向无环图,点编号为 \(1\) 到 \(n\),其中 \(1\) 号点被称为是根节点,除根节点以外,每个点都恰有一条出边(即以其作为起点的边)。每条边上有一个字符(这里我们实际上用一个不大于 \(300\) 的非负整数代表不同的字符),对于任意一个点 \(u\),\(u\) 的所有入边(即以其为终点的边)上的字符互不相同。
接下来我们定义往事,点 \(u\) 对应的往事为 \(u\) 到根的路径(显然有且只有一条)上的所有边按照从 \(u\) 到根经过的顺序排序后边上的字符依此拼接形成字符串,简记为 \(r(u)\)。
一棵往事树的联系度取决于它包含的所有往事之中最相近的一对相似度。具体地,我们定义两个点 和点 对应的往事的相似度 如下:
\(f(u,v) = LCP(r(u),r(v)) + LCS(r(u),r(v))\)
其中 \(LCP(a,b)\) 表示字符串 \(a\) 和 \(b\) 的最长公共前缀的长度,\(LCS(a,b)\) 表示字符串 \(a\) 和 \(b\) 的最长公共后缀的长度。
定义一棵往事树的联系度为所有满足 \(1\leq u<v\leq n\) 的 $f(u,v) $ 的最大值。
现在,给出一棵往事树,请你给出这棵往事树的联系度。
数据范围:\(n\leq 2\times 10^5\)
solution
树上后缀数组加线段树合并。
\(LCP(x,y)\) 其实就是 \(dep[Lca(x,y)]\) ,那我们的问题对于每个点 \(u\), 找子树中两个点 \(x,y\) 使得 \(LCP(r(x),r(y))\) 最大。
咕咕咕。



