省选模拟测试5
期望得分: \(100+40+30 = 170\)
实际得分: \(100+0+0 = 100\)
\(T1\) \(noip\) 难度的题,不说了。
\(T2\) 虽然正解是线段树合并,但自己却拿线段树合并优化暴力 \jk。
\(T3\) 本来打了 \(30\) 分的暴力分,但是出题人没造那一档的数据,然后我就愉快的爆零了。
T1 茶 a
题意描述
一开始,你拥有一个饼干,现在有三种操作
- 一种是将手里的饼干数量 \(+1\)
- 一种是将手里的 \(a\) 个饼干换成 1¥
- 一种是将 1¥换成 \(b\) 个饼干
求出在 \(k\) 次操作后最多有多少个饼干。
数据范围: \(k,a,b\leq 10^9\)
solution
水题,不说了。
注意特判各种情况就行。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
int k,a,b;
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
signed main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
k = read(); a = read(); b = read();
if(a >= b || k <= a) printf("%lld\n",k+1);
else
{
int tmp = a + (k-a+1)/2 * (b-a);
if((k-a+1)%2 == 1) tmp++;
printf("%lld\n",max(k+1,tmp));
}
fclose(stdin); fclose(stdout);
return 0;
}
T2 民族 b
题意描述
有\(n\) 座城市,一些民族。这些城市之间由 \(n-1\) 条有边权道路连接形成了以城市 \(1\) 为根的有根树。
每个城市都是某一民族的聚居地,已知第 \(i\) 个城市的民族是 \(a_i\),人数是 \(1\)。
我们定义一个民族 \(x\) 的来往程度 \(f(x)\) 为民族为 \(x\) 的点两两之间的距离之和,距离定义为树上两点间
最短路距离。
他想知道以 \(i\) 为根的子树内来往程度最大的民族 \(x\) 是多少,如果有多个,求编号最小。
以及对于给定的 \(k_i\) ,求 子树内编号的 \(k_i\) 小民族 \(y\) 的 \(f(y)\) 。
数据范围: \(n\leq 10^5, a_i\leq 10^5\)
solution
线段树合并/DSU。
我们把距离柿子拆一下变成: \(dis[x]+dis[y]-2\times dis[lca(x,y)]\) , \(dis[i]\) 表示根节点到 \(i\) 的边权和。
我们考虑那线段树合并来维护这个东西。
我们对于每个节点,开一个以民族编号为下标的权值线段树。
对于每个叶子节点 \(o\) ,设其民族编号为 \(x\), 维护如下信息:
- \(sum[o]\) 表示 \(f(x)\) 即民族编号为 \(x\) 的来往程度。
- \(w[o]\) 表示所有民族编号为 \(x\) 的点的 \(dis\) 之和。
- \(siz[o]\) 表示民族编号为 \(x\) 的点的个数。
- \(tag[o]\) 表示民族编号为 \(x\) 的点是否出现过。
对于非叶子节点 \(o\) 维护如下信息:
- \(sum[o]\) 表示 \(o\) 的子孙结点中叶子节点的 \(sum\) 最大值。
- \(id[o]\) 表示 \(o\) 的子孙节点中 \(sum\) 最大的叶子结点的编号是多少。
- \(tag[o]\) 表示 \(o\) 的子孙节点中叶子结点不为空的个数。
对于线段树合并的时候,我们只需要在叶子节点合并,其他的非叶子节点由儿子节点 \(up\) 一下即可。
假如说我们现在要把 \(rt[x]\) 和 \(rt[to]\) 两颗线段树合并,对两颗线段树的叶子节点 \(p,q\) 合并时,设合并之后的叶子节点为 \(p\) ,则有:
- \(sum[p] = sum[p] + sum[q] + siz[p]\times sum[q] + siz[q]\times sum[p] - 2\times siz[p]\times siz[q]\times dis[x]\)
- \(w[p] = w[p] + w[q]\)
- \(siz[p] = siz[p] + siz[q]\)
- \(tag[p] = tag[p] \ or \ tag[q]\)
我们只需要遍历一遍整棵树,维护出上述信息,对于询问 \(1\) 就是 \(tr[rt[x]].id\) ,对于询问 \(2\) ,我们只需要利用维护出的 \(tag\) 在线段树上二分即可。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int N = 1e5+10;
int n,cnt,tot,u,v,w,maxn;
int a[N],k[N],rt[N],head[N],sum[N],ans1[N],ans2[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
struct node
{
int to,net,w;
}e[N<<1];
struct Tree
{
int lc,rc;
int sum,siz,w,id,tag;
}tr[10000010];
void add(int x,int y,int w)
{
e[++tot].to = y;
e[tot].w = w;
e[tot].net = head[x];
head[x] = tot;
}
void up(int o)
{
tr[o].tag = tr[tr[o].lc].tag + tr[tr[o].rc].tag;
tr[o].sum = max(tr[tr[o].lc].sum,tr[tr[o].rc].sum);
if(tr[o].sum == 0)
{
if(tr[tr[o].lc].tag) tr[o].id = tr[tr[o].lc].id;
else tr[o].id = tr[tr[o].rc].id;
}
else tr[o].id = tr[o].sum == tr[tr[o].lc].sum ? tr[tr[o].lc].id : tr[tr[o].rc].id;
}
void insert(int &o,int l,int r,int x,int val)
{
if(!o) o = ++cnt;
if(l == r)
{
tr[o].w += val;
tr[o].siz++;
tr[o].tag = 1;
tr[o].id = l;
return;
}
int mid = (l+r)>>1;
if(x <= mid) insert(tr[o].lc,l,mid,x,val);
if(x > mid) insert(tr[o].rc,mid+1,r,x,val);
up(o);
}
void merage(int &x,int y,int l,int r,int root)
{
if(!x) {swap(x,y); return;}
if(!y) return;
if(l == r)
{
tr[x].sum = tr[x].sum + tr[y].sum + tr[x].w * tr[y].siz + tr[y].w * tr[x].siz - 2 * sum[root] * tr[x].siz * tr[y].siz;
tr[x].siz += tr[y].siz;
tr[x].tag |= tr[y].tag;
tr[x].w += tr[y].w;
return;
}
int mid = (l+r)>>1;
merage(tr[x].lc,tr[y].lc,l,mid,root);
merage(tr[x].rc,tr[y].rc,mid+1,r,root);
up(x);
}
int query(int o,int l,int r,int k)
{
if(l == r) return tr[o].sum;
int mid = (l+r)>>1;
int num = tr[tr[o].lc].tag;
if(k <= num) return query(tr[o].lc,l,mid,k);
else return query(tr[o].rc,mid+1,r,k-num);
}
void dfs1(int x,int fa,int w)
{
sum[x] = sum[fa] + w;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa) continue;
dfs1(to,x,e[i].w);
}
}
void dfs2(int x,int fa)
{
insert(rt[x],1,maxn,a[x],sum[x]);
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa) continue;
dfs2(to,x);
merage(rt[x],rt[to],1,maxn,x);
}
ans1[x] = tr[rt[x]].id;
if(tr[rt[x]].tag < k[x]) ans2[x] = -1;
else ans2[x] = query(rt[x],1,maxn,k[x]);
}
signed main()
{
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
n = read();
for(int i = 1; i <= n-1; i++)
{
u = read(); v = read(); w = read();
add(u,v,w); add(v,u,w);
}
dfs1(1,0,0);
for(int i = 1; i <= n; i++) a[i] = read(), maxn = max(maxn,a[i]);
for(int i = 1; i <= n; i++) k[i] = read();
dfs2(1,0);
for(int i = 1; i <= n; i++) printf("%lld %lld\n",ans1[i],ans2[i]);
fclose(stdin); fclose(stdout);
return 0;
}
T3 c
题意描述
给你三个整数 \(k,a,b\) ,满足 \(\gcd(a,b) = 1\) ,让你求不能被 \(ax+by, x\geq 0, y\geq 0\) 表示出来的第 \(k\) 大的数是多少。
数据范围:\(a,b\leq 5\times 10^7,k\leq 10^{18}\)
solution
首先有一个经典的结论:不能被 \(ax+by\) 表示出来的最大的数是 \(a\times b-a-b\) ,不能被表示出来的数的个数为 \((a-1)\times (b-1)\over 2\) 。
具体证明的话,我不太会证。
对于这道题我们可以先转化为求第 \(k\) 小的是多少,即: \(k = {(a-1)\times (b-1)\over 2}-k+1\)
我们把 \([1,a\times b-a-b]\) 分成若干块,每一块的长度均为 \(a\) ,如图:
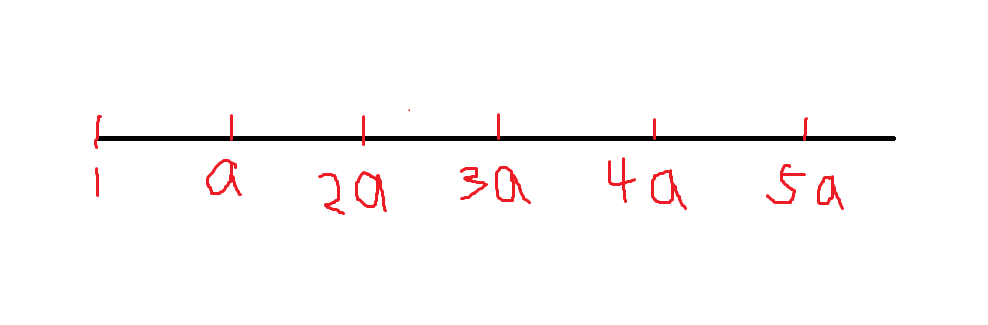
我们可以确定第 \(k\) 小的是在那一块,具体来说就是求一个 \(pos\) 使得 \(1-pos\times a\) 中不能被表示出来的数 \(\geq k\), \(1-(pos-1)\times a\) 中不能被表示出来的数 \(\leq k\) 。
那么我们怎么求 \(1-ia\) 中不能被表示出来的数的个数呢?这个我们可以转化为求能被表示出来的个数。
具体来说就是,设 \(sum[i]\) 表示 \(1-i\times a\) 中能被表示出来的数的个数。
则有递推式 :\(sum[i] = sum[i-1] + now + 1\), 其中 \(now\) 为 \(1-i\times a\) 中为 \(b\) 的倍数有多少个。
具体证明如下,首先 \([1,i\times a]\) 中能被表示出来的数的个数等价于 \([(i-1)\times a+1,i\times a]\) 这一段区间能被表示出来的数的个数加上 \([1,(i-1)\times a]\) 这一段区间能被表示出来的个数。
对于 \([1,(i-1)\times a]\) 这一段区间能被表示出来的数的个数就是 \(sum[i-1]\) 。
对于 \(by_1\) ,我们可以使他加上 \(ax1\) 使得 \((i-1)\times a \leq ax_1+by_1\leq i\times a\) 。
这样的 \(by_1\) 共有 \(now\) 个,又因为 \(\gcd(a,b) = 1\) ,可知 \(ax_1+by_1\) 是不会重复的。
所以 \([(i-1)\times a,i\times a]\) 这一段区间可以被表示出来的数的个数为 \(now+1\), \(+1\) 则是因为 \(i\times a\) 也可以被表示出来。
因此,我们的递推式 \(sum[i] = sum[i-1]+now+1\) 是正确的。
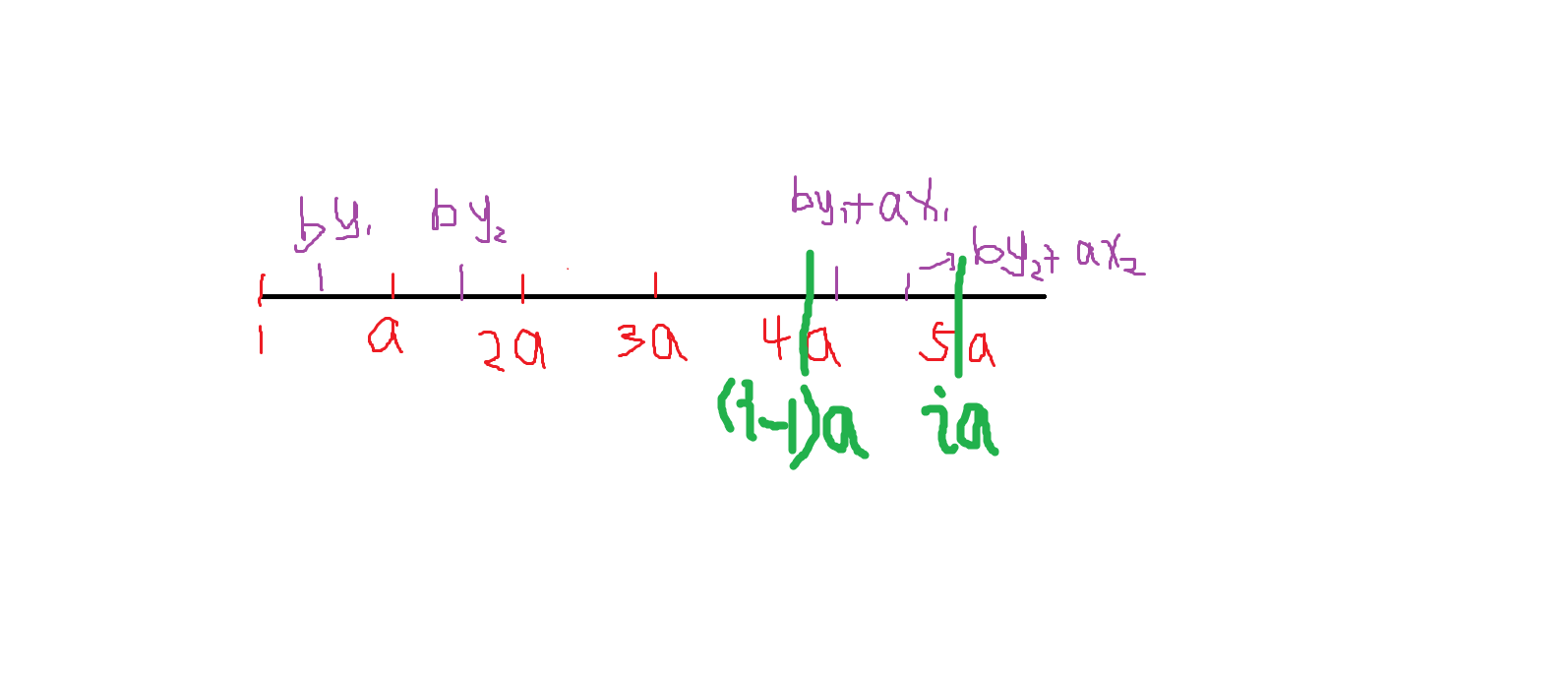
那么有了 \(sum[i]\) ,我们的 \(pos\) 就很好求出来了。
求出来 \(pos\) 之后,我们先用 \(k\) 减去 \([1,(pos-1)\times a]\) 中不能被表示出来的数的个数,然后 \([(pos-1)\times a+1,pos\times a]\) 中第 \(k\) 个不能被表示出来的数,就是我们的答案。
又因为每一块的元素不超过 \(a\) 个,所以我们可以枚举 \([(pos-1)\times a+1,pos\times a]\) 这一段区间中的数,来判断它是否是第 \(k\) 个不能被表示出来的数。
那么怎么判断数 \(s\) 是否可以被表示出来呢?
很简单,因为 \(s\) 可以被表示出来,等价于 \(s=ax+by\) 即: \(s\equiv by\pmod a\) ,所以我们在枚举 \(b\) 的倍数的时候把 \(by\% a\) 标记为 \(1\), 如果 \(s\%a\) 被标记过,那么 \(s\) 就可以被表示出来。
然后我们这道题就做完了。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<map>
using namespace std;
#define int long long
int a,b,k,cnt,now,sum,pos;
bool vis[50000010];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
signed main()
{
freopen("c.in","r",stdin);
freopen("c.out","w",stdout);
a = read(); b = read(); k = read();
k = ((a-1)*(b-1)/2)-k+1; vis[0] = 1;
for(int i = 0; ; i++)
{
while((now+1)*b <= i*a) now++, vis[(now*b)%a] = 1;
if(i*a-sum-now >= k)
{
pos = i;
break;
}
sum += now + 1;
}
k -= (pos-1)*a-sum+1;//这里+1是因为0也可以被表示出来
for(int i = (pos-1)*a+1; i <= pos*a; i++)
{
if(!vis[i%a]) k--;
if(k == 0)
{
printf("%lld\n",i);
return 0;
}
}
fclose(stdin); fclose(stdout);
return 0;
}


