计算几何全家桶

解析几何初步

在计算几何中，一般都是浮点数在运算，所以我们一般要设个精度值，比如 \(1e-8\) 就好了。

处理精度:

const double eps = 1e-8;
int dcmp(double x)//处理精度，判断正负 
{
	if(fabs(x) < eps) return 0;
	if(x < 0) return -1;
	return 1;
}

点与向量

平面直角坐标系上的点一般表示成 \(P(x,y)\)，其中 \(x\),\(y\) 为点的坐标。

我们记录其横纵坐标值即可。用 \(pair\) 或开个结构体记录均可。

向量和点是一样的，为了区分我们 \(typedf\) 就好了。

例如 ：

struct point//点或向量
{
	double x,y;
	point(double X = 0, double Y = 0){x = X, y = Y;}
};
typedef point Vector
pair<double,double> ponit;

向量的坐标表示和点相同，所以只需要像点一样存向量即可。

任意两点之间 \(P_1(x_1,y_1),P_2(x_2,y_2)\) 的距离记为 $|P_1P_2| $， 由勾股定理可知：

\(|P_1P_2| = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\).

double dis(point a,point b)//两点距离
{
	return (double) sqrt((a.x-b.x) * (a.x-b.x) + (a.y-b.y) * (a.y-b.y))
} 

直线

众所周知，两点确定一条直线，所以我们只需要记录一下直线上的两个点就行。

直线可以用直线上一个点 \(P_0\) 和方向向量 $v $ 来表示， 且直线上所有点 \(P\) 都满足 \(P = P_{0} + tv\) 。

\(t\) 叫做参数。如果说直线上两个点分别为 \(A\) 和 \(B\) ,则方向向量为 \(B-A\), 且 \(P = A + t(B-A)\)

例如：

struct Line
{
	point A,B;
	Line(point a,point b){A = a, B = b;}
}

线段

线段很好记录：只记录左右端点就可以。

和上面直线的存储一样。

struct Segment
{
	point A,B;
	Segment(point a,point b) {A = a, B = b;} 
} 

多边形

由三条或三条以上的线段首尾顺次连接所组成的封闭图形叫做多边形。

一般来说，我们记录多边形只需要开个数组，按顺序存储多边形的每个顶点即可。

struct point
{
	double x,y;
	point(double X = 0, double Y = 0){x = X, y = Y;}
}p[N];

圆

一条线段绕着他的一个端点（圆心）在平面旋转一周时，他的另一个端点的轨迹叫做圆，线段的长度叫做圆的半径。设圆心坐标为 \(（x_0,y_0）\) ,半径为 \(r\) ,则圆的标准方程为： \((x-x_0)^2+(y-y_0)^2 = r^2\)

存储一个圆的话，只需要保存他的圆心坐标以及半径即可。

以 \((x_0,y_0)\) 为圆心，\(r\) 为半径的圆的参数方程为：

\(\left\{\begin{aligned} x&=x_0+r\cos\theta\\ y&=y_0+r\sin\theta \end{aligned}\right.\)

然后我们就可以根据这个来求出圆上所有点的坐标。

例如：

struct circle
{
	point p;//圆心 
	double r;
	circle(point A,double B){p = A, r = B;}
}

三角和差公式

\(\sin(a + \theta) = \sin a\cos \theta + \cos a\sin \theta\)

\(\sin(a-\theta) = \sin a\cos \theta - \cos a\sin \theta\)

\(\cos(a + \theta) = \cos a\cos \theta - \sin a\sin \theta\)

\(\cos(a - \theta) = \cos a \cos \theta + \sin a\sin \theta\)

极角和极坐标系

我们在平面上选一个点 \(O\), 称为极点，自极点引出一条射线 \(Ox\) 称为极轴，再选择一个单位长度（数学中常为 \(1\) ）,一个角度（通常为弧度），以及其正方向（通常为逆时针方向），这样就建立了极坐标系。

在极坐标系中，设 \(A\) 为平面上一点，极点 \(O\) 和 \(A\) 之间的距离 \(|OA|\) 为极径，记为 \(\rho\) ,以极轴为始边， \(OA\) 为终边的角 \(\angle xOA\) 为极角，记为 \(\beta\) ,那么有序序对 \((\rho,\beta)\) 即为 \(A\) 的极坐标。

有些时候我们需要把极坐标系转化到平面直角坐标系下去研究，两者转化关系如下：

点 \(A(\rho,\theta)\) 的直角坐标 \((x,y)\) 可以表示为： \(\left\{\begin{aligned} \rho \cos\theta&=x\\\rho\sin\theta&=y\end{aligned}\right.\)

进而可知： \(\left\{\begin{aligned} \rho^2 &=x^2 + y^2\\\tan\theta&={y\over x}\end{aligned}\right.\)

于是极角 $\theta = \arctan{y\over x} $ ,然后这样就可以求出极角了。

如果题目中要求反正切函数，尽量使用 \(atan2({y,x})\) ,这个函数用途比 \(atan(x)\) 要广。

来张图就很好理解了

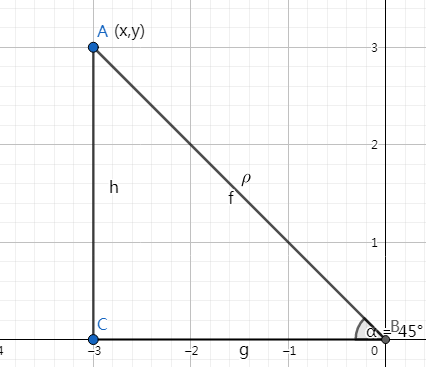
矢量及其运算

矢量指的是有方向的线段，也称向量，即线段两个端点 \(P_1\) 和 \(P_2\) 的顺序是有关系的，记为 \(\vec{P_1P_2}\), 设 \(a = \vec{P_1P_2}\) ,

则有向线段的长度称为矢量的模，记作 \(|a|\)。 如果 \(P_1\) 为坐标原点，则 \(\vec{P_1P_2}\) 又称为矢量 \(P_2\) .

矢量的模长

若向量 \(\vec a = (x,y)\) , 则 \(|a| = \sqrt{x^2+y^2} = \sqrt{|\vec a|^2}\)

double len(point a)//向量的模长 
{
	return (double) sqrt(a.x * a.x + a.y * a.y);
}

矢量的加减法

想必大家在高中的时候都学过吧，这里我只给出公式，就不再细说了。

对于 \(\vec a = (x_1,y_1)\), \(\vec b = (x_2,y_2)\) , 则 \(\vec a + \vec b = (x_1+x_2,y_1+y_2)\)

对于 \(\vec a = (x_1,y_1)\), \(\vec b = (x_2,y_2)\), 则 \(\vec a -\vec b = (x_1-x_2,y_1-y_2)\)

point operator + (point a,point b) {return point(a.x+b.x,a.y+b.y);}
point operator - (point a,point b) {return point(a.x-b.x,a.y-b.y);}

向量的数乘

对于 $\vec a = (x,y) $ , \(\lambda\vec a = (\lambda x,\lambda y)\)

point operator * (point a,double k) {return point(a.x*k,a.y*k);}//数乘

矢量的数量积

两个矢量的数量积，又称点乘，其结果是一个数，大小等于这两个矢量的模长的乘积，再乘以他们夹角的余弦，即： \(a \cdot b = |a||b|\cos<a,b>\) .

对于 \(\vec a = (x_1,y_1)\) , \(\vec b = (x_2,y_2)\) , \(\vec a \cdot \vec b = (x_1x_2+y_1y_2)\)

夹角 \(\theta\) 与点积大小的关系 (可以结合三角函数理解一下)：

1. 若 \(\theta = 0\) , 则 \(\vec a\cdot \vec b = |a||b|\)
2. 若 \(\theta = 180^\circ\) ,则 \(\vec a \cdot \vec b = -|a||b|\)
3. 若 \(\theta < 90^\circ\), 则 \(\vec a\cdot \vec b > 0\)
4. 若 \(\theta = 90^\circ\), 则 \(\vec a \cdot \vec b = 0\)
5. 若 \(\theta > 90^\circ\), 则 \(\vec a\cdot\vec b < 0\)

double Dot(point a,point b){return a.x*b.x+a.y*b.y;}//点积 

满足一下几个性质：

交换律： \(\vec a \cdot \vec b = \vec b\cdot \vec a\)

分配律： \(\vec a\cdot (\vec b + \vec c) = \vec a\cdot \vec b + \vec a \cdot \vec c\)

结合律： \((m\vec a) \cdot \vec b = m (\vec a\cdot \vec b) = \vec a \cdot (m\vec b)\)

矢量的矢量积

两个矢量的矢量积，又称叉乘叉积，其结果是一个向量。矢量 \(a\) 和矢量 \(b\) 叉乘的几何意义为：他的模长等于由 \(a\) 和 \(b\) 组成的平行四边形的面积，方向与四边形所在平面垂直。 即： \(|\vec a \times \vec b| = |\vec a||\vec b| \sin<a,b>\) 。

对于 \(\vec a = (x_1,y_1 )\) ， \(\vec b = (x_2,y_2)\), \(\vec a\times \vec b = (x_1y_2-x_2y_1)\) (交叉相乘)

![](

)

如图所示，向量位置与叉积模长大小的关系：

1. 若 \(\vec a\times \vec b = 0\) ，则 \(\vec a\) 和 \(\vec b\) 共线，方向相同或相反。
2. 若 \(\vec a\times \vec b > 0\) , 则 \(\vec a\) 在 \(\vec b\) 的顺时针方向。
3. 若 \(\vec a\times \vec b < 0\) , 则 \(\vec a\) 在 \(\vec b\) 的逆时针方向.

double Cro(point a,point b){return a.x*b.y-a.y*b.x;}//叉积的模长 

注意 \(\sin\) 函数的符号，如果 \(\vec a\) 在 \(\vec b\) 的顺时针方向，那么 \(\sin<\vec a,\vec b>\) 就是正值，否则为负值，记住一句话：顺正逆负即可。

又因为前面乘的是绝对值，所以叉积的符号就是 \(\sin\) 函数的符号。

叉积的应用

三角形面积公式：\(S_{\Delta ABC} = ab\sin C\)

因此，三角形的面积就是任意两条临边的叉积绝对值的一半。

同理，平行四边行的面积就是两条临边对应向量的叉积的绝对值。

类似的，任意四边形的面积等于两条对角线的叉积的绝对值的一半。

向量的旋转

\(v^\prime = (x\cos a - y\sin a, x\sin a + y\cos a)\) .

其中 \(a\) 表示你逆时针旋转的弧度。这个公式比较容易忘，建议熟记。

如果实在记不住，就把直角坐标转化为极坐标，在把角度加上 \(a\) 之后再转回来（其实这个公式就是这么来的）。

point retate(point a,double altha)
{
	return point(a.x * cos(altha) - a.y * sin(altha),a.x * sin(altha) + a.y *cos(altha));
}

例题： uva11178

图形与图形之间的关系

点与线段

判断点是否在线段上

做法1： 点 \(p\) 在线段 \(AB\) 上，当且仅当 \(|PA| + |PB| = |AB|\)

做法2：先利用叉积判断点是否在线段所在的直线上（叉积为 0），在用点积判断点是否在线段上（点积小于等于 0） 即可。如果点在线段的端点上点积等于零，否则点积小于零。

一般来说，做法 \(1\) 损失的精度比较大，所以我们一般采用做法 2.

bool pd_PS(point p,point A,point B)//判断 p 是否在 线段 AB 上 
{
//	return dis(p,A) + dis(p,B) == dis(A,B);//这种做法精度损失较大。
	return (dcmp(Cro(p-A,p-B)) == 0) &&(dcmp(Dot(p-A,p-B) <= 0));
}

口胡：如果说 \(p\) 在线段 \(A B\) 的外部，显然 \(\vec {AP}\) 和 \(\vec {BP}\) 是同向的，点积为正，反之，逆向为负。

点到线段的距离

从 \(P\) 向 \(AB\) 直线，做一条垂线，设垂足为 \(Q\) 。

若 \(Q\) 在线段 \(AB\) 上，则点 \(P\) 到线段 \(AB\) 的距离为 \(PQ\) 。

如果 \(Q\) 在射线 \(BA\) 上，则所求距离为 \(PA\) 的长度，否则为 \(PB\) 的长度。

如果 \(\angle PAB\) 和 \(\angle PBA\) 均为锐角或直角，则 \(Q\) 在线段 \(AB\) 上，若 \(\angle PAB\) 为钝角，则 \(Q\) 在射线 \(BA\) ,若 \(\angle PBA\) 为钝角，则 \(Q\) 在射线 \(AB\) 上 ，利用点积可以很好的判断出来。

可以自己画一下图理解一下。

double dis_PS(point p,point A,point B)//点到直线的距离
{
	if(Dot(p-A,B-A) < 0) return dis(p,A);//垂足离A更近
	if(Dot(p-B,A-B) < 0) return dis(p,B);//垂足离B更近
	return abs(Cro(A-p,B-p))/dis(A,B);//垂足的距离最小
}

例题： UVA10263 Railway

判断两线段是否相交(不包括交点)

如果两个线段相交，则必然有一条线段的两个端点在另一条线段的两侧。

利用叉积判断即可。

bool pd_SS(point A,point B,point C,point D)//线段 AB 和线段 CD 是否相交 
{
	double f1 = Cro(C-A,B-A), f2 = Cro(D-A,B-A);//第一条线段的两个端点是否在第二条线段的两侧 
	double g1 = Cro(A-C,D-C), g2 = Cro(B-C,D-C);//第二条线段的两个端点是否在第一条线段的两侧 
	return ((f1 < 0) ^ (f2 < 0)) && ((g1 < 0) ^ (g2 < 0));
} 

点与直线

点与直线的距离

如图所示我们要求点 \(A\) 到直线 \(BC\) 的距离：

我们连接 \(AB\) 和 \(AC\) ,在做 \(A\) 关于 直线 \(BC\) 的垂线，设垂足为 \(D\)

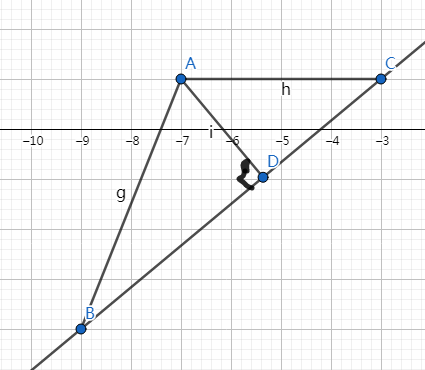
则有 \(2S_{\Delta ABC} = AD * BC\) .

点 \(A\) 到直线的距离 \(AD\) 则为 \(2S_{\Delta ABC} \over BC\) ,用一个柿子表示出来就是：\(AD = {|\vec {AB} \times \vec {AC}| \over |\vec{BC}|}\)

double dis_PL(point p,point A,point B)//点到直线 AB 的距离 
{
	return abs(Cross(p-A,p-B)) / len(A-B);//面积除以底 
}

点在直线上的垂足（投影）

直线 \(AB\) 的参数式: \(A + tv\), 点 \(P\) 的垂足 \(Q\) 的参数为 \(t_0\), 根据 \(\vec {QP} \perp \vec {AB}\) ，则有：

\[Q = A + t_0 v\\ (P-Q)\cdot v = 0\\ (P - A - t_0v) \cdot v = 0\\ (P-A) \cdot v - t_0v \cdot v = 0\\ t_0 = {(P-A) \cdot v\over v \cdot v}\\ \]

point GetLineRoot(point p,point A,point B)//p在直线AB上的投影 
{
	point v = B - a;//方向向量v 
	return A + v * (Dot(P-A,v) / Dot(v,v));
}

点在直线的那一边

假设 直线上一点 \(P\) 方向向量为 \(v\) ,则 \(Q\) 在直线的那一边可以用 \(\vec {PQ} \times v\) 来判断。叉积为负，\(Q\) 在直线上方，

叉积为零，在直线上，叉积为正，\(Q\) 在直线下方。

点关于直线的对称点

先找到点 \(P\) 关于直线的垂足 \(Q\), 然后把 \(PQ\) 延长两倍即可。

point Symmetry_PL(point p,point A,point B)//p关于直线AB的对称点
{
	return p + (GetLineRoot(p,A,B)-p) * 2;//把Q延长两倍	
} 

例题：P4468 [SCOI2007]折纸

线与线

两直线交点

设两直线方程分别为： \(l_1 = P + t\vec v\) , \(l_2 = Q + t\vec w\) 。

则： 交点在第一条直线的参数为 $ t $ ,则 \(t = {(P-Q) \times \vec w \over \vec w \times \vec v}\) 。

因为是交点，所以同时满足两个直线的方程，令交点在两条直线上的参数分别为 \(t\) 和 \(\mu\) ,

则有：\(P + t \vec v = Q + \mu \vec w\) 。

两边同时叉上 \(\vec w\) 可得： \((P + t\vec v)\times \vec w = (Q + \mu\vec w)\times \vec w\) 。

去括号可得： \(P\times \vec w + t\vec v \times\vec w = Q\times \vec w + \mu \vec w \times \vec w\) 。

又因为 \(\vec w \times \vec w = 0\), 所以可得： \(P \times \vec w + t\vec v \times \vec w = Q \times \vec w\)

移项可得： \(t\vec v \times \vec w = (Q-P)\times \vec w\)

所以： \(t = {(P-Q)\times \vec w\over \vec w \times \vec v}\) 。

point jiao_LL(point A,point B,point C,point D)//线段AB和线段CD的交点 
{
	point v = B - A, w = D - C, PQ = A - C;//直接套用公式就ok了 
	double t = Cro(PQ,w) / Cro(w,v);
	return A + t * v;
}//用的时候记得要特判一下两直线是否平行

点与多边形

判断点是否在多边形内

设凸 \(n\) 边形的顶点为 \(P_0P_1....P_n\) ，以及点 \(A\)。 记 \(\theta_i = <\vec{AP_i},\vec{AP_{i+1}}>\)， 则 点 \(A\) 在多边形内部等价于 \(\displaystyle\sum_{i=0}^{n-1} \theta_i = 2π\)

需要特判一下在多边形顶点上的情况。

point p[1005];
int n;
bool InPloygon(point A)//精度损失会比较大一些 
{
	double alpha = 0;
	for(int i = 1; i <= n; i++)
	{
		if(i == n) alpha += fabs(Angle(p[i]-A,p[1]-A));
		else alpha += fabs(Angle(p[i]-A,p[i+1]-A));
	}
	return dcmp(alpha-2 * pai) == 0;
}

例题： UVA109 SCUD Busters

判断点是否在凸多边形内部

给你 \(m\) 个点和由 \(n\) 个点组成的凸多边形，问你这 \(m\) 个点是否在凸多边形内部。

如果用上面的转角法和射线法来判断的话，复杂度为 \(O(nm)\) 的。

有没有一个更高效的算法呢？我们可以用二分来做到 \(O(mlogn)\) 的。

首先任选一个点为起点，向凸多边形其他顶点做一条射线。如图：

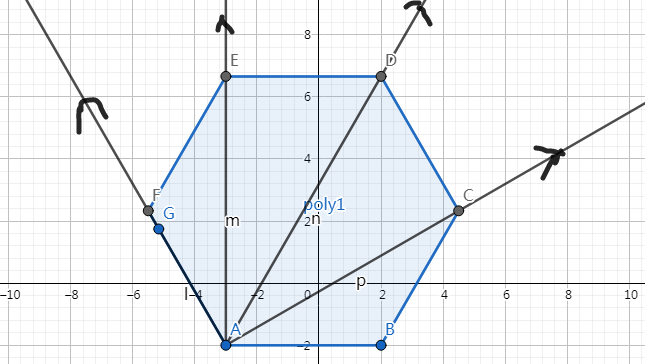
显然，会把整个凸多边形分成 \(n-2\) 个三角形。

第二步：判断这个点是否在所有射线的包含范围之内，即判断定点是否在最左侧射线的左边或者最右侧射线的右边。

第三部：二分出定点在那个三角形内部，然后判断定点是否在这个三角形内部即可。

int InPolygn(point p,point *a)
{
	if(Cro(p-a[1],a[2]-a[1]) < 0 || Cro(p-a[1],a[n]-a[1]) > 0) return 0;//在边界外 
	if(pd_PS(p,a[1],a[2]) || pd_PS(p,a[n],a[1])) return 2;//在边界上 
	int l = 2, r = n;
	while(r - l > 1)
	{
		int mid = (l + r)>>1;
		if(Cro(p-a[1],a[mid]-a[1]) < 0) l = mid;
		else r = mid;
	}
	if(Cro(p-a[l],a[r]-a[l]) > 0) return 0;//在边界外 
	if(pd_PS(p,a[l],a[r])) return 2;//在边界上 
	return 1;
}

圆

判断点是否在圆内

很简单，判断点到圆心的距离和圆的半径大小即可。

过定点做圆的切线

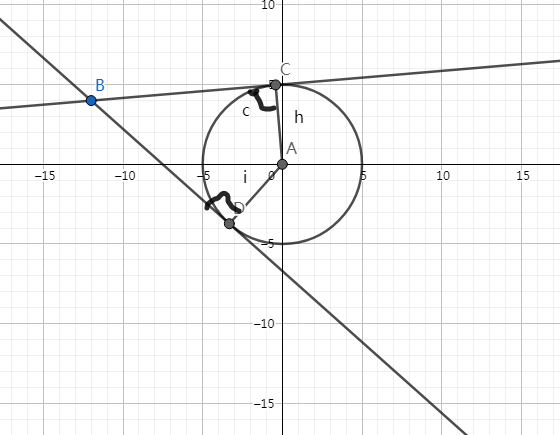
我们先求出 \(AB\) 的长度和 \(AC\) 的长度，然后可以根据这个求出来 \(\angle CBA\) .

那么两条切线就是 直线 \(AB\) 顺时针（逆时针） 旋转 \(\angle CBA\) 形成的直线。

int get_PC(point p,Circle c,line *v)//返回交点个数，v存储切线 
{
	Vector u = c.p - p;//BA向量 
	double dis = dis(p,c.p);
	if(dis < r) return 0;
	else if(dcmp(dis,r) == 0)//点在圆上的情况 
	{
		v[0] = retate(u,PI/2);
		return 1;
	}
	else//点不在圆上的情况 
	{
		double ang = asin(c.r/dis);
		v[0] = retate(u,ang);
		v[1] = retate(u,-ang);
		return 2;
	}
}

两个圆的交点

point get(Circle c,double a)//返回c圆上圆心角为a的点的坐标 
{
	return point(c.x+cos(a)*c.r,c.y+sin(a)*r);
}
double Angle(point a){return atan2(a.x,a.y);}
int getCC(Cirle c1,Cirle c2,vector<point>& sta)//返回交点个数，sta存交点的坐标 
{
	double d = len(c1.c-c2.c);
	if(cdmp(d) == 0)
	{
		if(dcmp(c1.r-c2.r) == 0) return -1//两个圆重合 
		return 0;//没有交点 
	}
	if(dcmp(c1.r+c2.r-d) < 0) return 0;//没有交点的情况 
	if(dcmp(fabs(c1.r-c2.r)-d) > 0) return 0;
	double alpha = Angle(c2.c-c1.c);
	double deta = acos((c1.r*c1.r+d*d-c2.r*c2.r)/(2*c1.r*d));//余弦定理算夹角 
	point p1 = get(c1,alpha-deta);
	point p2 = get(c1,alpha+deta);//旋转 
	sta.push_back(p1);
	if(p1 == p2) return 1;
	sta.push_back(p2);
	return 2;
}

三角形重心

三点各坐标的平均值： \(({x_1+x_2+x_3\over 3}, {y_1+y_2+y_3\over 3})\)

图形面积

任意多边形面积

因为从第一个顶点出发可以把多边形分为 \(n-2\) 个三角形，多边形的面积就是这 \(n-2\) 个三角形的面积之和，直接叉积计算即可。

因为你叉积运算的时候是带符号的，所以你计算结果可能是面积也可能是 面积的相反数，取个绝对值就行了。

在你计算复杂多边形的面积的时候，多算的面积就会被叉积的符号抵消掉。

double PloyArea(point *a,int n)
{
	double res = 0;
	for(int i = 2; i < n; i++) res += Cro(a[i]-a[1],a[i+1]-a[1]);
	return abs(res / 2);//如果你提前按极角排一下序，就可以省去取绝对值这一步
}

P1183 多边形的面积

自适应辛普森法

用来求定积分。

当函数极为鬼畜的时候，我们采用二次拟合的形式，当精度相等的时候，便视为相等。

假如说我们要求 \(\int_{a}^{b} f(x) d(x)\) ,你现在要求出这个函数的近似值。

我们可以把这个函数近似成矩形和梯形和等等。我们为了保证准确性，这里选择二次函数来拟合曲线。

设 \(f(x) \approx Ax^2 + Bx+ C\)

\(\int_{a}^{b} f(x)d(x) \approx \int_{a}^{b} Ax^2+Bx+C\)

\(= \int_{a}^{b} Ax^2 + \int_{a}^{b} Bx + \int_{a}^{b} C\)

\(={A\over 3}x^3 + {B\over 2}x^2 + Cx|_{a}^{b}\)

\(={(a-b)\over 6} (2A(a^2+ab+b^2) + 3B(a+b) + 6C)\)

\(={a-b\over 6} ((Aa^2+Ba+c) + (Ab^2+Bb+c) + 4(({a+b\over 2})^2 + {a+b\over 2} + c))\)

$ = {a-b\over 6} (f(a) + f(b) + 4f({a+b\over 2}))$

然后就有个结论： $$\int_a^{bf(x)dx\approx\int_a}(Ax^2+Bx+C)dx=\frac{(a-b)(f(a)+f(b)+4f(\frac{a+b}{2}))}{6}$$

这样直接算的话，我们的精度误差会很大，我们考虑吧 \([a,b]\) 从终点分为两部分 \([a,mid],[mid,b]\) 来计算。

当 \(\int_{a}^{mid} f(x)d(x) + f_{mid}^{b}f(x)d(x) = f_{a}^{b}f(x)d(x) + eps\) 时，便停止递归。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const double eps = 1e-12;
double a,b,c,d,l,r;
double f(double x){return 1.0*(c*x+d)/(a*x+b);}
double calc(double l,double r)
{
	double mid = (l +r)/2.0;
	return (r-l)*(f(l)+f(r)+4*f(mid))/6;
}
double simpon(double l,double r,double last)
{
	double mid = (l + r)/2; 
	double lx = calc(l,mid), rx = calc(mid,r);//递归算左右侧的积分
	if(fabs(lx + rx - last) < eps) return lx+rx;//lx+rx-last<eps 说明我们l-r这一段的积分的值误差小到可以忽略
	else return simpon(l,mid,lx) + simpon(mid,r,rx);//这个你可以理解为simpon把l-r这一段划分成了若干个小段，l-r这一段的积分等于这些小段积分的和。
}
int main()
{
	scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&l,&r);
	printf("%.6lf\n",simpon(l,r,calc(l,r)));
	return 0;
}

例题： 板子1 板子2

计算几何的基本算法

凸包

现在平面上有一堆点，让你找到一个点集，依次连接这些点，组成一个多边形，且所有的点都在这个多边形内部或边上，这个多边形我们称之为凸包。

就相当于平面上有很多钉子，你拿一个橡皮筋一围，围出来的多边形就是凸包。

大概张这个样子：

然后观察一下这个凸包，你会发现一下很好玩的性质。

• 上凸壳中的点的斜率是单调递减的。
• 下凸壳中的点的斜率的单点递增的。

这个性质有什么用呢？ 他主要是用来斜率优化的。

Graham 扫描算法

首先我们发现最下面的一个点肯定会在凸包上。所以一开始我们可以通过一遍扫描把这一个点找出来记做点 \(A\) (如果有多个从坐标相同的点都在最下方，则取最左边的点)。

第二步：把所有的点按 \(Ap_i\) 的极角大小进行排序，极角相同的按照到点 \(A\) 的距离来排序。

第三步：维护一个栈，来保存当前凸包的形态。将每个点按顺序依次加入凸包中。如果当前这个点 \(P\) 和栈顶的两个顶点 \(B,C\)。如果 \(\vec{BC}\) 在 \(\vec{PC}\) 的逆时针方向，显然 \(B\) 点肯定不在凸包上， 然后每加入一个点，都重复上述步骤，排除不符合的点即可。

顺时针的情况为什么不考虑呢？因为可能是在拐弯处。

口胡说的不太清楚，拿一些图演示一下。

（1）首先给你一堆点， 最下面的点 \(p_1\) 肯定是在凸包里面的，然后把所有的点按极角排序，编号。

（2）然后 \(P_2\) 准备入栈，由于栈中元素过少，所以符合条件，可以直接进栈。

（3）之后因为 \(\vec {P_2P_1}\) 在 \(\vec{P_3P_1}\) 的 顺时针方向，符合条件，暂时把他加进去

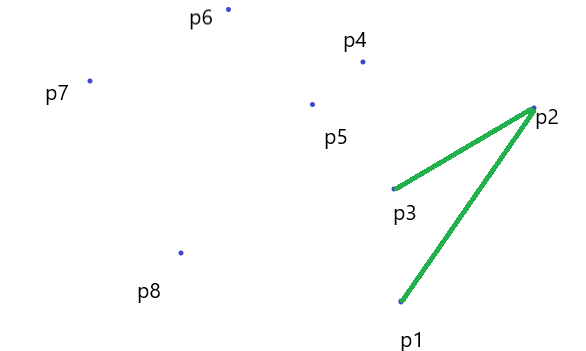
（4）之后 \(\vec {P_3P_2}\) 在 \(\vec{P_4P_2}\) 的逆时针方向，就把 \(P_3\) 出栈，再去检查 \(P_2\) 符合条件，于是 \(P_4\) 入栈。

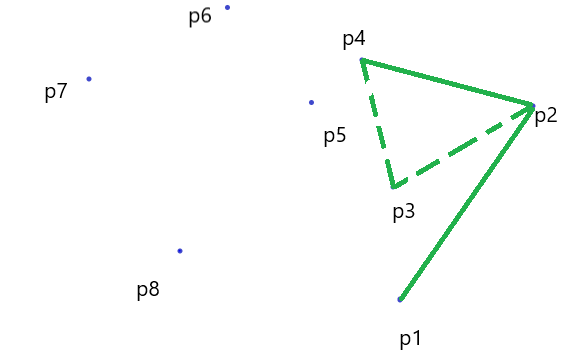
（5） \(P_5\) 一切正常，入栈。

（6） \(P_6\) 这里就麻烦多了，首先 \(\vec{P_5P_4}\) 在 \(\vec{P_6P_4}\) 的逆时针方向，把 \(P_5\) 出栈

（7） 又发现 \(\vec{P_4P_2}\) 在 $\vec{P_6P_2} $ 的逆时针方向，把\(P_4\) 出栈。

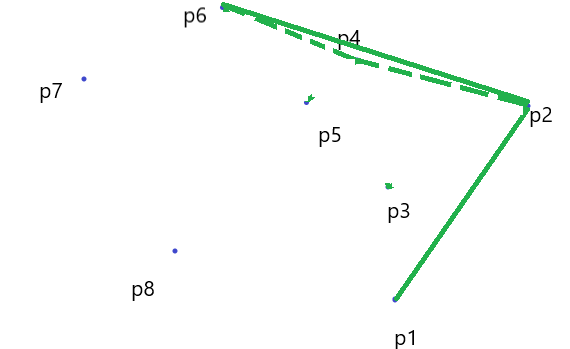
（8） \(P_7\) 一切正常，入栈

（9）\(P_8\) 一切正常，入栈

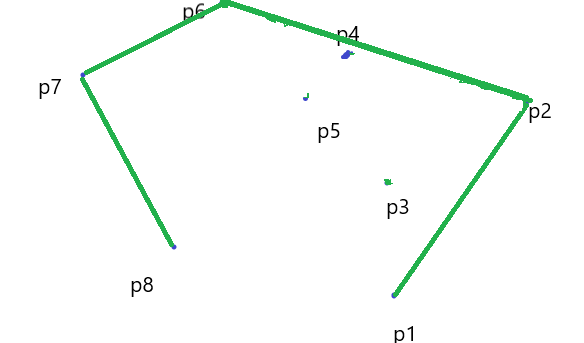
(10) 最后就连到了 起点 \(P_1\) ，我们的凸包就求出来了。

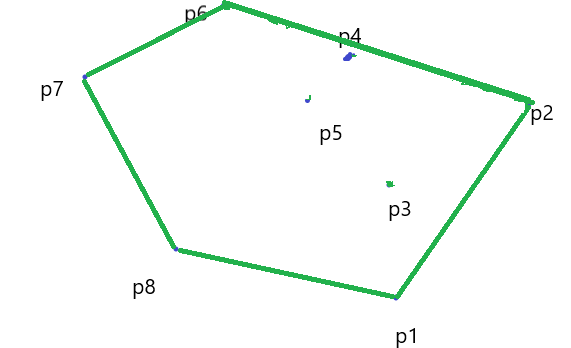
#include<iostream>
#include<cstdio> 
#include<algorithm>
#include<cmath>
using namespace std;
const double eps = 1e-8;
int n,top;
double ans;
struct point
{
	double x,y;
	point(double X = 0, double Y = 0){x = X, y = Y;}
}p[100010],sta[100010];
point operator + (point a,point b){return point(a.x+b.x,a.y+b.y);}
point operator - (point a,point b){return point(a.x-b.x,a.y-b.y);}
point operator * (point a,double b){return point(a.x*b,a.y*b);}
double Dot(point a,point b){return a.x*b.x+a.y*b.y;}
double Cro(point a,point b){return a.x*b.y-a.y*b.x;}
int dcmp(double x)
{
	if(fabs(x) < eps) return 0;
	if(x > 0) return 1;
	return -1; 
}
double dis(point a,point b)
{
	return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y) * (a.y-b.y));
}
bool comp(point a,point b)
{
	double m = Cro(a-p[1],b-p[1]);//由叉积来判断极角大小，如果a的极角比b小，那么ap一定在bp的顺时针方向
	if(dcmp(m) > 0) return 1;
	if(dcmp(m) == 0 && dcmp(dis(a,p[1])-dis(b,p[1])) < 0) return 1;
	return 0;
}
int main()
{
	scanf("%d",&n);
	for(int i = 1; i <= n; i++)
	{
		scanf("%lf%lf",&p[i].x,&p[i].y);
		if(dcmp(p[i].y-p[1].y) < 0) swap(p[1],p[i]);
		else if(dcmp(p[i].y-p[1].y) == 0 && dcmp(p[i].x-p[1].x) < 0) swap(p[1],p[i]);
	}
	sort(p+2,p+n+1,comp);
	sta[++top] = p[1]; sta[++top] = p[2];
	for(int i = 3; i <= n; i++)
	{
		while(top >= 2 && Cro(sta[top]-sta[top-1],p[i]-sta[top-1]) <= 0) top--;
		sta[++top] = p[i];
	}
	for(int i = 1; i < top; i++) ans += dis(sta[i],sta[i+1]);
	ans += dis(sta[top],sta[1]);
	printf("%.2lf\n",ans);
	return 0;
}

例题： 模板 信用卡凸包

Graham 水平序扫描法

这个其实是上面那种算法的变种。一般来说这个是要比上面那个算法是快的，并且精度也比较高。

第一步：先把所有的点按横坐标为第一关键字纵坐标为第二关键字排序（这个和上面是不同的，这也是水平序比极角序要快的原因）。

第二步：从前往后扫一遍得到下凸壳。

第二步：从后往前倒着扫一遍得到上凸壳。

来张图模拟一下：

排完序之后的点集如图：

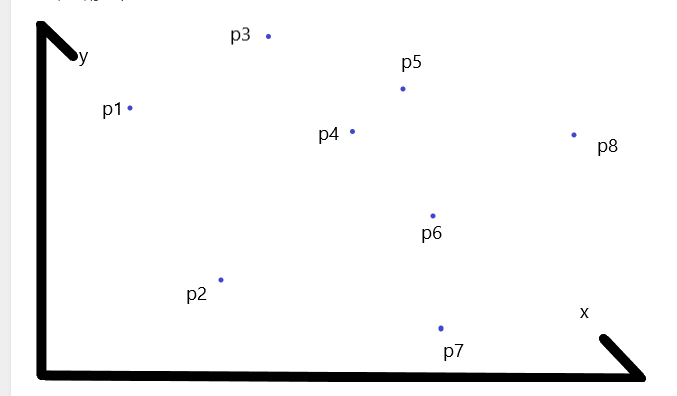
首先，我们先把前两个点入栈

• 因为 \(p_1\) 的横坐标是最小的，所以他一定实在凸包上的
• \(P_2\) 无法确定，等之后在判断。

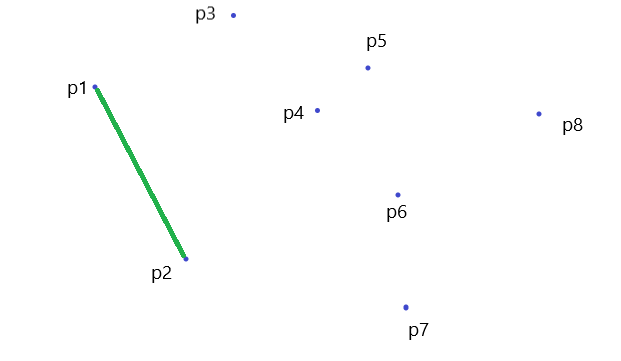
$ P_1P_2P_3$ 组成的是一个凸多边形，所以 \(P_3\) 合法，入栈

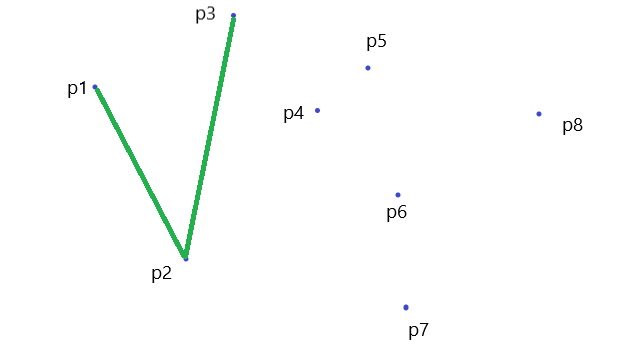
\(P_4\) 与 \(P_3\) 的连线在 \(P_2P_3\) 的逆时针方向，于是 \(P_3\) 出栈，检查 \(P_2\) 合法，之后 \(P_4\) 入栈。

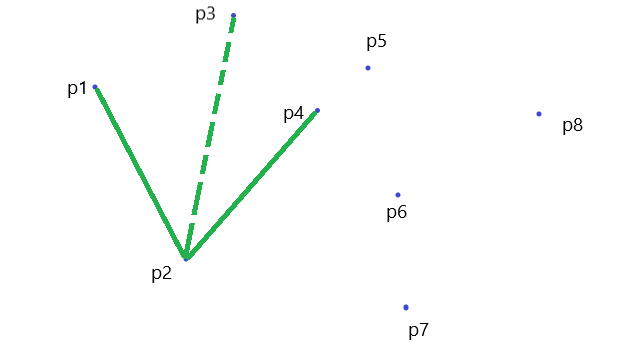
同理： \(P_4\) 出栈，\(P_5\) 入栈

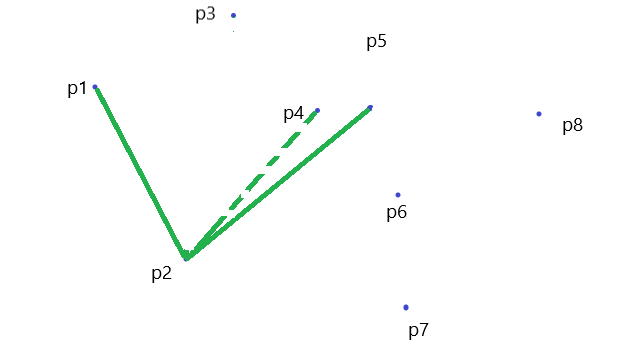
\(P_5\) 出栈，\(P_6\) 出栈

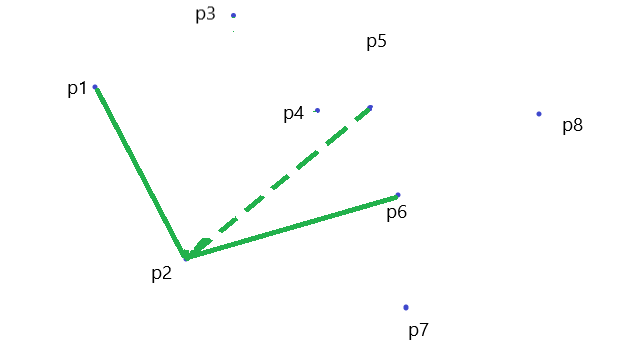
\(P_6\) 出栈， \(P_7\) 入栈

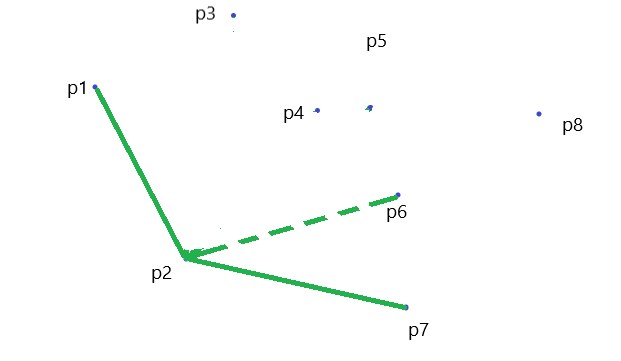
\(P_8\) 入栈

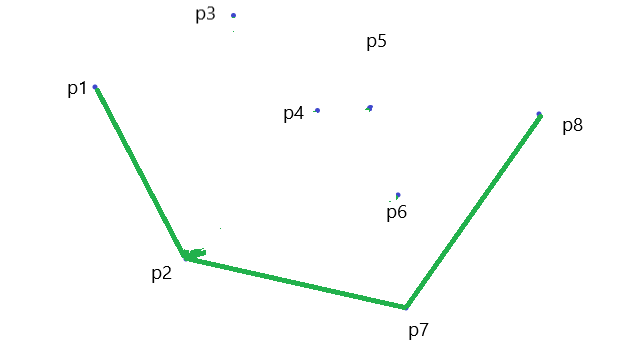
有木有发现一个很严重的问题，扫描到最后，我们只求出来个下凸壳。

那么上凸壳怎么求呢，很简单，倒着再跑一遍即可。

最后求出来的凸包长这样:

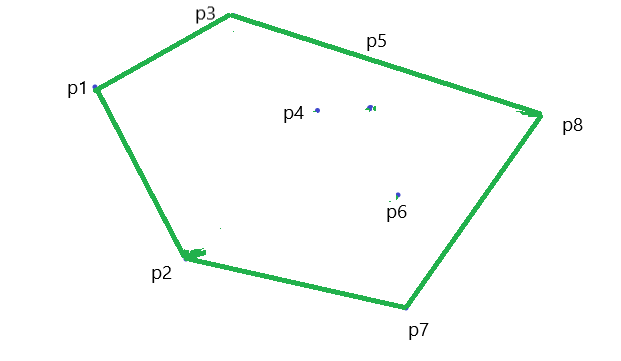
最后栈中的元素为： \(P_1,P_2,P_7,P_8,P_8,P_5,P_3,P_1\)

你会发现起点和终点在栈中出现了两次，但自己到自己的距离为零，所以不会对答案产生影响。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm> 
using namespace std;
const int N = 1e5+10;
const double eps = 1e-8;
int n,top;
double ans;
struct point
{
	double x,y;
	point(){}
	point(double a,double b){x = a, y = b;}
}p[N],sta[N];
point operator + (point a,point b){return point(a.x+b.x,a.y+b.y);}
point operator - (point a,point b){return point(a.x-b.x,a.y-b.y);}
point operator * (point a,double k){return point(a.x*k,a.y*k);}
double Dot(point a,point b){return a.x*b.x+a.y*b.y;}
double Cro(point a,point b){return a.x*b.y-a.y*b.x;}
double dis(point a,point b)
{
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int dcmp(double x)
{
	if(fabs(x) < eps) return 0;
	return x > 0 ? 1 : -1;
}
bool comp(point a,point b)
{
	if(dcmp(a.x-b.x) == 0) return a.y < b.y;
	return a.x < b.x;
}
int main()
{
	scanf("%d",&n);
	for(int i = 1; i <= n; i++) scanf("%lf%lf",&p[i].x,&p[i].y);
	sort(p+1,p+n+1,comp);
	sta[++top] = p[1]; sta[++top] = p[2];
	for(int i = 3; i <= n; i++) //下凸壳
	{
		while(top >= 2 && Cro(sta[top]-sta[top-1],p[i]-sta[top-1]) < 0) top--;
		sta[++top] = p[i];
	}
	int last = top;
	sta[++top] = p[n]; sta[++top] = p[n-1];//上凸壳
	for(int i = n-2; i >= 1; i--)
	{
		while(top - last >= 2 && Cro(sta[top]-sta[top-1],p[i]-sta[top-1]) < 0) top--;
		sta[++top] = p[i];
	}
	for(int i = 1; i < top; i++) ans += dis(sta[i],sta[i+1]);//起点和终点都在栈中出现了两次
	printf("%.2lf\n",ans);
	return 0;
}

动态凸包

先来道板子题： 防线修建

我们考虑加入一个点之后，会对当前的凸包产生什么影响。

如图我们当前凸包长这样：

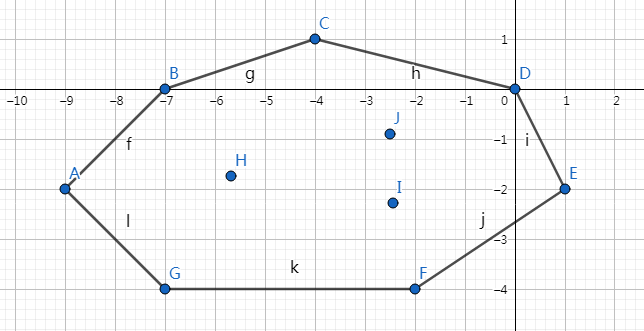
当我们加入一个点 \(G\) 的时候，图中紫色的线就是新的凸包增加的那一部分。

根据静态凸包的构造方法（Anderw扫描法）：

1. 将各点坐标以横坐标为第一关键字，纵坐标为第二关键字排序。
2. 维护一下上凸壳和下凸壳。拿维护上凸壳举例，注意到如果之前有两点 \(A\) 和 \(B\) ，当插入新节点 \(C\) 时，如果 \(\overrightarrow{AB} \times \overrightarrow{AC} ≥0\) 时，这说明 \(B\) 在线段 \(AC\) 的下方，就可以将 \(B\) 删除。我们可以看出此时凸包是一个类似单调栈的结构。

我们拿 \(set\) 维护一下这个凸壳，当我们加入一个点的时候，检查一下周围的点是否会被删除即可。

显然每加入一个点，被删除的只能是他在 \(set\) 中的前驱和后继。

这个题我们离线一下，倒着做，就只需要动态维护一个上凸壳，比较好写点.

感觉自己写的时候，尽量画个图参照着写，不然的话你就很容易搞混。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<set>
using namespace std;
const int N = 1e5+10;
const double eps = 1e-8;
int n,m,cntq;
double x,y,last;
bool vis[N];
struct node
{
	int opt,c;
	double ans;
}q[N];
struct point
{
	double x,y;
	double ang;
	point(){}
	point(double a,double b){x = a, y = b;}
	friend bool operator < (point a,point b)
	{
		if(a.x == b.x) return a.y < b.y;
		return a.x < b.x;
	}
}p[N],o;
int dcmp(double x)
{
	if(fabs(x) < eps) return 0;
	return x > 0 ? 1 : -1;
}
point operator + (point a,point b){return point(a.x+b.x,a.y+b.y);}
point operator - (point a,point b){return point(a.x-b.x,a.y-b.y);}
point operator * (point a,double k){return point(a.x*k,a.y*k);}
double Dot(point a,point b){return a.x*b.x+a.y*b.y;}
double Cro(point a,point b){return a.x*b.y-a.y*b.x;}
double dis(point a,point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
set<point> s;
void insert(point now)
{
	set<point>::iterator itl,itr,tmp;
	itr = s.lower_bound(now);//itl 是他的前驱，itr是他的后继
	itl = itr; --itl;
	if(Cro(now-*itl,*itr-*itl) > 0) return;//如果这个点在凸包内的话就不用进行任何操作
	last -= dis(*itl,*itr);
	while(itr != s.end())//s.end返回的是set最后一个元素的下一个位置
	{
		tmp = itr; ++itr;//tmp指now的后继，itr为now的后继的后继
		if(itr == s.end() || Cro(now-*itr,*tmp-*itr) < 0) break;//可以参考上面的那个图理解一下
		last -= dis(*tmp,*itr);//把这条边从答案中减去
		s.erase(tmp);//tmp这个点不在凸包中了
	}
	while(itl != s.begin())
	{
		tmp = itl; --itl;//tmp为now的前驱，itl为now的前驱的前驱
		if(Cro(now-*itl,*tmp-*itl) > 0) break;
		last -= dis(*tmp,*itl);//把这条边的贡献从答案中减去
		s.erase(tmp);
	}
	s.insert(now);
	itl = itr = s.find(now);
	--itl; ++itr;//找now在凸包中的上一个点和下一个点
	last += dis(now,*itl) + dis(now,*itr);
}
int main()
{
	scanf("%d%lf%lf",&n,&x,&y);
	point a = point(0,0);
	point b = point(n,0); 
	point c = point(x,y);
	s.insert(a); s.insert(b); s.insert(c);
	last += dis(b,c) + dis(c,a);
	scanf("%d",&m);
	for(int i = 1; i <= m; i++) scanf("%lf%lf",&p[i].x,&p[i].y);
	scanf("%d",&cntq);
	for(int i = 1; i <= cntq; i++)
	{
		scanf("%d",&q[i].opt);
		if(q[i].opt == 1)
		{
			scanf("%d",&q[i].c);
			vis[q[i].c] = 1;
		}
	}
	for(int i = 1; i <= m; i++) if(!vis[i]) insert(p[i]);//先把所有没被消灭的点加入凸包中
	for(int i = cntq; i >= 1; i--)
	{
		if(q[i].opt == 1) insert(p[q[i].c]);
		else q[i].ans = last;
	}
	for(int i = 1; i <= cntq; i++) if(q[i].opt == 2) printf("%.2lf\n",q[i].ans);
	return 0;
}

旋转卡壳

这个他的原理是什么呢？主要是在一个凸包上，他的很多函数都是单峰的。比如固定一条多边形的边，其他的点和这条边组成的面积是单峰的。

求凸包直径

凸包的直径：定义凸包上任意两点之间距离的最大值。

怎么求？ 暴力枚举 $O(n^2) $

有一个结论：如果一个点到一条边的距离最远，那么点到线段两端点中一个的距离一定是最远的。

优化一下，首先我们可以固定一条边，然后点到这条边的距离是一个单峰的函数，显然我们是可以三分出来的，复杂度 \(O(nlogn)\)。

继续优化，旋转卡壳利用了一个更好的性质,假设说我们固定的这条边是不断滚动的，如图：

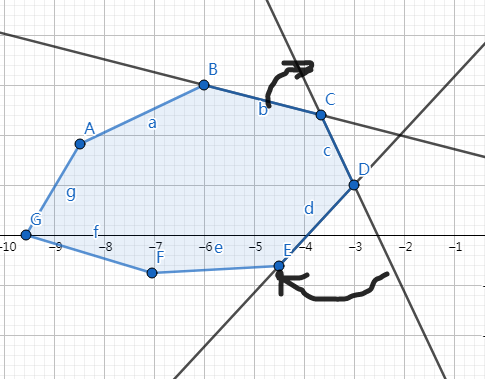
先固定 \(BC\) 这条边，在固定 \(CD\), 之后接着固定 \(DE\) ,之后.....

你会发现，当你固定 \(BC\) 这条边的时候，如果 \(E\) 没有 \(F\) 优，那么当你固定 \(CD\) 的时候， \(E\) 肯定不会比 \(F\) 优。

也就是说：我们的边是顺时针的枚举，而此时距离他们最远的点也是顺时针的出现！！

然后我们就可以通过双指针扫一遍就可以得到这个凸包的直径。

基本上旋转卡壳就是这么一个流程。

一个动图演示一下：

double Get_zhijing()
{
	double res = 0;
	sta[top + 1] = p[1];//把 sta[top]sta[1] 这条边也要加进去 
	for(int i = 1, j = 2; i <= top; i++)
	{
		while(Cro(sta[i]-sta[j],sta[i+1]-sta[j]) < Cro(sta[i]-sta[j+1],sta[i+1]-sta[j+1])) j = j % top + 1;//找距离 sta[i]sta[i+1] 最远的点
		res = max(res,max(dis(sta[i],sta[j]),dis(sta[i+1],sta[j])));
	}
	return res;
}

例题：旋转卡壳

最小矩形覆盖

让你找一个矩形使得这个矩形能覆盖住点集中所有的点，且矩形的，面积最小。

怎么求？暴力枚举 \(O(n^4)\) .

考虑到这个矩形他肯定有一条边是会和凸包的一条边重合的（这个并不好证，但反正他是正确的）

当我们固定一条边的时候，我们还需要知道，每个点到这条边投影的最大值和最小值（矩形的左右侧），和点到这条边距离的最大值（矩形的上底边）。

结合图理解一下：

假如说，我们要求这个多边形的最小矩形覆盖：

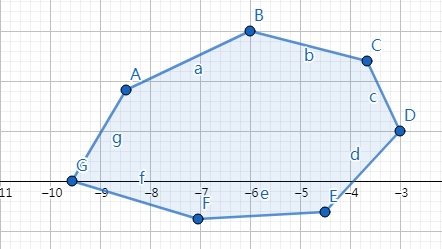
当我们固定 \(DE\) 这条边的时候，我们最小的矩形长这样：

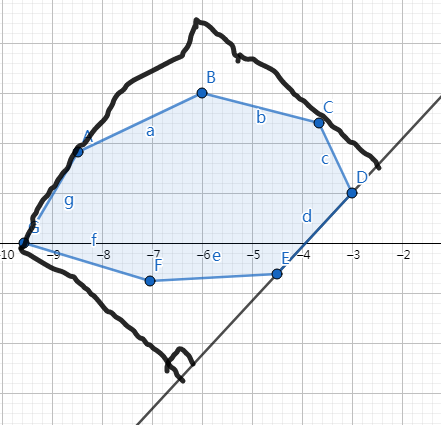
很容易发现，矩形的高就是点到 \(ED\) 距离的最大值，矩形的宽就是点到 \(ED\) 这条直线投影的最小值和最大值的差。

这三个东西，都可以拿旋转卡壳维护出来 (也可以在凸包上三分)，复杂度 \(O(n)\)

半平面交

如图：一条直线把平面分为了两部分，我们通常把直线的左侧平面称为他的半平面。

如下图所示，直线 \(P_1P_2\) 的半平面就是黄色的部分。

注意直线的方向不同，所构成的半平面也是不同的，因此在做半平面交的时候要注意一下方向问题。

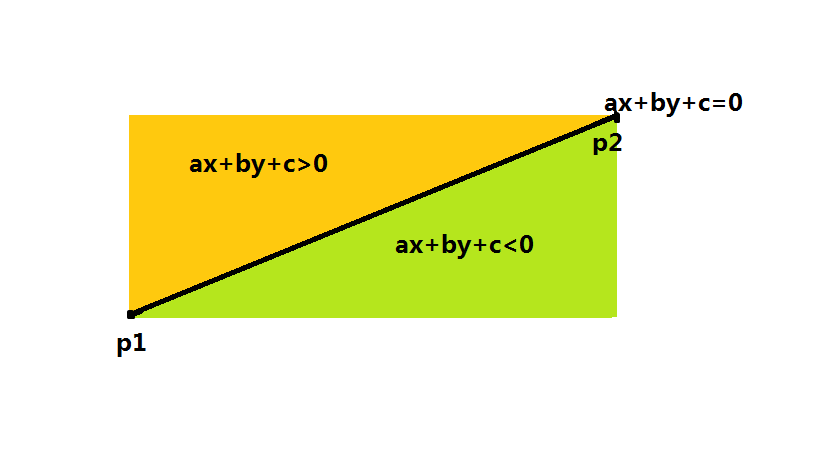
半平面交：多个半平面同时覆盖的区域叫做半平面交，如图，红色区域就是那三条直线的半平面交。

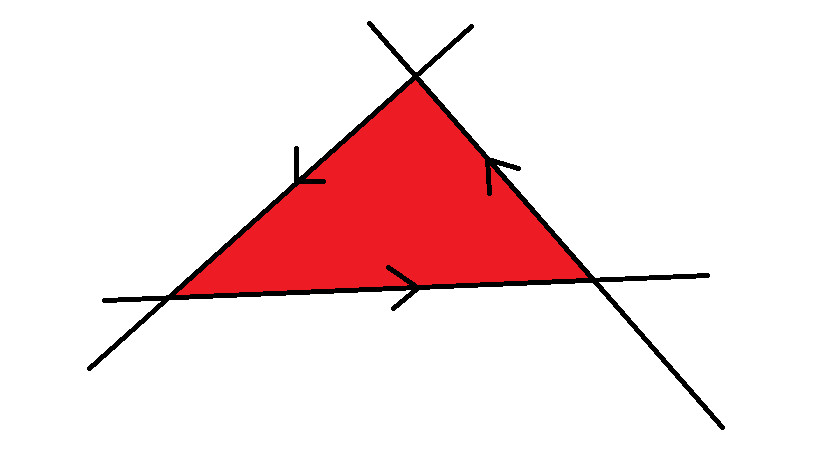
我们还可以观察到，第一个图中直线 \(P_1P_2\) 的半平面区域 \(ax+by+c > 0\) ,而直线 \(P_2P_1\) 的半平面区域

则是 \(ax+by+c < 0\) .

所以半平面交的本质就是方程组：$a_ix+b_iy+c > 0 $ 或 \(a_ix+b_iy+c < 0\) 的合法解的区域（这好像是线性规划的柿子）。

一般半平面交的题都是让你列出等式，然后构造半平面交求解。

怎么求？

我们发现半平面交的区域是一个凸多边形（或者空集，线段）。

计算半平面交的一个好方法就是增量法，即初始答案为整个平面，然后注意加入各个平面，维护当前的半平面交。

一开始我们像凸包那样把所有的直线按极角排一下序，这样可以保证我们当前合法的直线的交就是我们的半平面交，然后考虑依次加入每一条线段。

我们开两个队列，一个维护合法的直线，另一个维护半平面交的交点，以便确定半平面交的形态。

如果前面两条合法直线 \(A,B\) 的交点在这条直线 \(C\) 的右侧，那么直线 \(A\) 和 直线 \(B\) 组成的平面交会被 直线 \(C\) 覆盖掉一部分，那么直线 \(B\) 就不合法了，把他从队列中弹出来即可，同时在第二个队列中把 \(A\) 和 \(B\) 的交点出队， 重复上述过程，直到之前加入的直线都合法为止。最后在把直线 \(C\) 和 \(AC\) 的交点入队即可。

如图：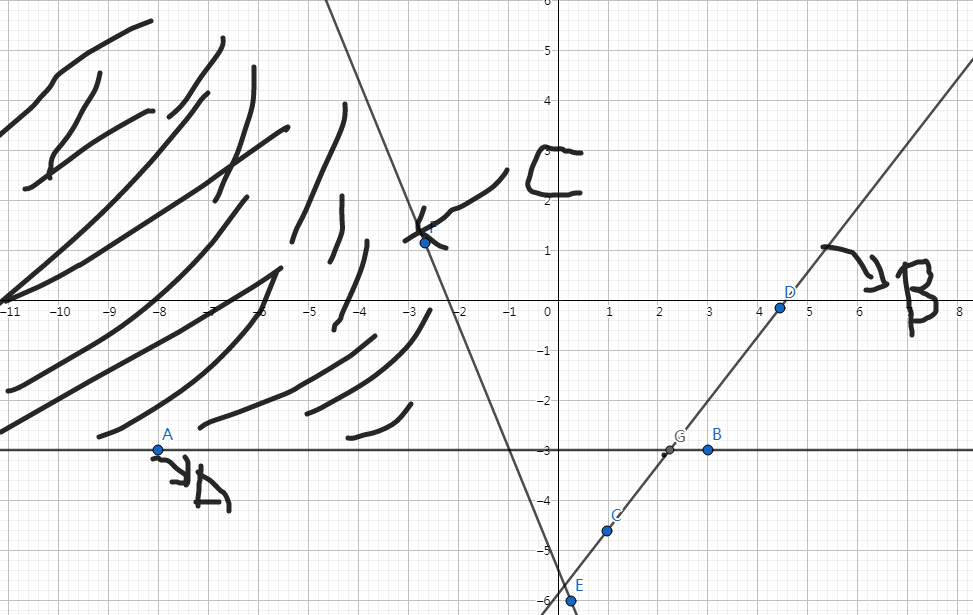

如果交点 \(G\) 在直线左侧，说明我们队列中所有的直线都是合法的，这时候，我们把直线 \(C\) 以及他与 \(B\) 的交点入队即可。

因为最后我们要围成一个多边形，所以你现在加入的这一条直线可能会使对首的直线不合法，举个例子：

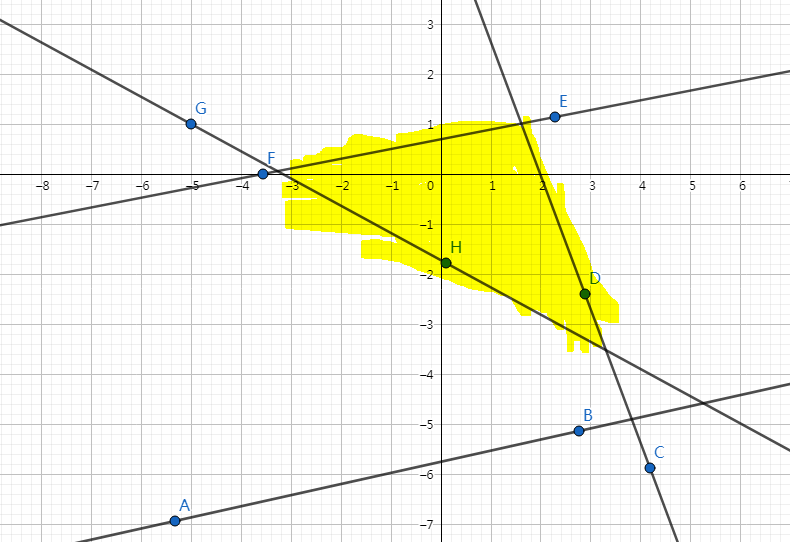
当我们加入 \(DH\) 这条直线的时候，合法的半平面交的区域是图中的黄色部分，显然直线 \(AB\) 不在这个区域内。

那么我们需要开个双端队列来维护一下，每次加入一条直线的时候，检查队头和队尾，去除不合法的元素即可。

当我们半平面交是无限大的时候怎么办？如图：

这时候我们在一开始可以人为地加入四条边界直线，这样半平面交就不会无限大啦。

愉快的代码时间：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const double lim = 1000.0;
const double eps = 1e-8;
const int N = 1e5+10;
int n,m,l,r,cnt;
double area;
struct point
{
	double x,y;
	point(){}
	point(double a,double b){x = a, y = b;}
}sta[N],p[N],ans[N];
typedef point Vector;
struct line
{
	point x,y;
	double ang;
	line(){}
	line(point a,point b)
	{
		x = a; y = b;
		ang = atan2(b.y-a.y,b.x-a.x);
	}
}L[N],q[N];
point operator + (point a,point b){return point(a.x+b.x,a.y+b.y);}
point operator - (point a,point b){return point(a.x-b.x,a.y-b.y);}
point operator * (point a,double k){return point(a.x*k,a.y*k);}
double Dot(point a,point b){return a.x*b.x+a.y*b.y;}
double Cro(point a,point b){return a.x*b.y-a.y*b.x;}
double dis(point a,point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
bool OnRight(point p,line s){return Cro(p-s.x,s.y-s.x) > 0;}
int dcmp(double x)
{
	if(fabs(x) < eps) return 0;
	return x > 0 ? 1 : -1;
}
bool comp(line a,line b)
{
	if(a.ang == b.ang) return OnRight(b.x,a);
	return a.ang < b.ang;
}
point Root_LL(line a,line b)
{
	Vector v = a.y-a.x, u = b.y-b.x, w = a.x-b.x;
	double t = Cro(w,u)/Cro(u,v);
	return a.x + v * t;
}
int HPI()
{
	int m = 0;
	sort(L+1,L+cnt+1,comp);
	l = 1, r = 1; q[1] = L[1];
	for(int i = 2; i <= cnt; i++)
	{
		if(dcmp(L[i].ang - L[i-1].ang) == 0) continue;
		while(l < r && OnRight(sta[r-1],L[i])) r--;
		while(l < r && OnRight(sta[l],L[i])) l++;
		q[++r] = L[i]; 
		if(l < r) sta[r-1] = Root_LL(q[r],q[r-1]);
	}
	while(l < r && OnRight(sta[r-1],q[l])) r--;//删去多余的点
	while(l < r && OnRight(sta[l],q[r])) l++;
	if(r - l + 1 <= 2) return 0;
	sta[r] = Root_LL(q[l],q[r]);
	for(int i = l; i <= r; i++) ans[++m] = sta[i];
	return m;
}
int main()
{
	scanf("%d",&n);
	for(int i = 1; i <= n; i++)
	{
		scanf("%d",&m);
		for(int j = 1; j <= m; j++) scanf("%lf%lf",&p[j].x,&p[j].y);
		for(int j = 1; j < m; j++) L[++cnt] = line(p[j],p[j+1]);
		L[++cnt] = line(p[m],p[1]);
	} 
	point a = point(-lim,lim);
	point b = point(-lim,-lim);
	point c = point(lim,-lim);
	point d = point(lim,lim);
	L[++cnt] = line(a,b); L[++cnt] = line(b,c); L[++cnt] = line(c,d); L[++cnt] = line(d,a);
	n = HPI();
	for(int i = 2; i < n; i++) area += Cro(ans[i]-ans[1],ans[i+1]-ans[1]);
	printf("%.3lf\n",area/2);
	return 0;
}

随机增量法

随机增量算法是计算几何的一个重要算法，它对理论知识要求不高，算法时间复杂度低，应用范围广大。(扯淡)

增量法 (Incremental Algorithm) 的思想与第一数学归纳法类似，它的本质是将一个问题化为规模刚好小一层的子问题。解决子问题后加入当前的对象。写成递归式是： \(T(n) = T(n-1)+g(n)\)。 --------wiki

直接看题吧：最小圆覆盖

首先，假设说我们已经求出来了前 \(i-1\) 个点的最小圆覆盖，现在我们要新加入一个点 \(i\) ,如果点 \(i\) 在最小圆内，好继续往里面加点，否则的话第 \(i\) 个点肯定在新的最小圆上。

这时候我们需要求出过点 \(i\) 且覆盖前 \(i-1\) 个点的最小圆。

由于三点确定一个圆，所以我们还需要确定一下其余的两个点。

第一步：不断枚举不在最小圆上的点 \(j\), 来扩大我们最小圆的面积,此时的圆心为 \(i+j\over 2\) ,半径为 \(dis(i,j)\)， 之后做过 \(i,j\) 两个点且覆盖前 $j-1 $ 个点的最小圆。

第三步：枚举剩下的 \(j-1\) 个点 \(k\)，如果 \(k\) 不在最小圆中，过 \(i,j,k\) 三个点的圆，这个圆就是过 点 \(i\) 且覆盖前 \(k\) 个点的最小圆。

复杂度分析：

上述的是期望复杂度，一般情况下出题人可能会造一些数据卡掉这种解法。

肿么办，random_shuffle 一下即可。 \(n^3\) 过百万。

至于怎么求过三个点的最小圆，你可以尝试解方程（反正太复杂了，我没看懂，第二篇题解有证明），你也可以做中垂线，求两条直线的交点。

#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-15;
int n;
double r;
struct point
{
	double x,y;
	point(){}
	point(double a,double b){x = a, y = b;}
}p[100010],o;
typedef point Vector;
struct line
{
	point x,y;
	line(){}
	line(point a,point b){x = a, y = b;}
};
point operator + (point a,point b){return point(a.x+b.x,a.y+b.y);}
point operator - (point a,point b){return point(a.x-b.x,a.y-b.y);}
point operator * (point a,double k){return point(a.x*k,a.y*k);}
double Dot(point a,point b){return a.x*b.x+a.y*b.y;}
double Cro(point a,point b){return a.x*b.y-a.y*b.x;}
point retate(point a){return point(a.y,-a.x);}//向量顺时针旋转90.
double dis(point a,point b)
{
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int dcmp(double x)
{
	if(fabs(x) < eps) return 0;
	return x > 0 ? 1 : -1;
}
line ZhongChuiXian(point a,point b)
{
	point v = retate(b-a);
	point A = point ((a.x+b.x)/2,(a.y+b.y)/2);
	return line(A,v);
}
point Root_LL(line a,line b)
{
	Vector v = a.y, u = b.y, w = a.x-b.x;
	double t = Cro(w,u)/Cro(u,v);
	return a.x + v * t;
}
point get(point a,point b,point c)
{
	line s1 = ZhongChuiXian(a,b);
	line s2 = ZhongChuiXian(b,c);
	return Root_LL(s1,s2);	//两个点中垂线的交点
}
int main()
{
	srand(time(0)); rand();
	scanf("%d",&n);
	for(int i = 1; i <= n; i++) scanf("%lf%lf",&p[i].x,&p[i].y);
	for(int i = 1; i <= n; i++)
	{
		int l = rand() % n + 1;
		int r = rand() % n + 1;
		swap(p[l],p[r]);
	}
	o = p[1]; r = 0;
	for(int i = 2; i <= n; i++)//做覆盖前 i个点的最小圆
	{
		if(dcmp(dis(p[i],o)-r) <= 0) continue;
		o = p[i]; r = 0;//如果第i个点不在之前的最小圆上，那么点i一定在新的最小圆上
		for(int j = 1; j < i; j++)//做过点i，且覆盖前i-1个点的最小圆
		{
			if(dcmp(dis(p[j],o)-r) <= 0) continue;//不断往里面加点
			o.x = (p[i].x+p[j].x)/2;
			o.y = (p[i].y+p[j].y)/2;
			r = dis(p[i],o);
			for(int k = 1; k < j; k++)//做过点i和点j且覆盖前j-1个点的最小覆盖圆
			{
				if(dcmp(dis(p[k],o)-r) <= 0) continue;//不断的往里面加点
				o = get(p[i],p[j],p[k]);//三个点确定一个圆
				r = dis(p[i],o); 
			}
		}
	}
	printf("%.10lf\n",r);
	printf("%.10lf %.10lf\n",o.x,o.y);
	return 0;
}

例题：信号塔

闵可夫斯基和

就是说，平面上有两个凸包 \(A\) 和 \(B\) ,如图：

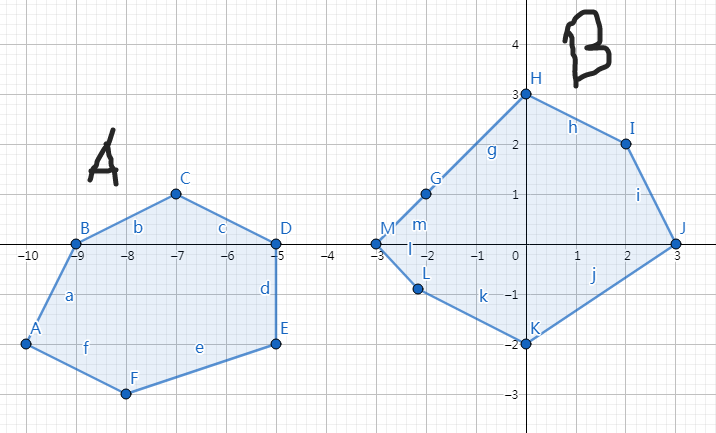
每个凸包可以看做一个点集。

定义两个凸包的闵可夫斯基和 $A+B = {\alpha + \beta }, \alpha\in A,\beta\in B $ 。

也就是说我们从 \(A\) 和 \(B\) 中任选两个点出来，在把这两个点的横纵坐标相加，把得到的新的点放到一个集合中，这个集合就叫做两个凸包的闵可夫斯基和。

如下图，粉色区域就是三角形和四边形的闵可夫斯基和。

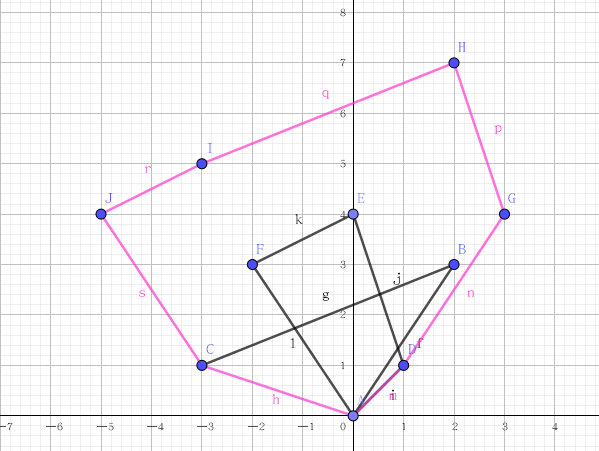
结论1：闵可夫斯基和是凸性的。

证明：

一个多边形是凸性的，等价于 \(\alpha ,\beta\in A, x\beta+(1-x)\alpha \in A\) 。

也就是说如果 \(\alpha\) 和 \(\beta\) 在这个多边形内，那么 \(\alpha\beta\) 这一条线段上所有的点也是在这一个凸多边形上的。

有 \(\alpha_1\alpha_2\in A,\beta_1\beta_2\in B\) ，则有 \(\alpha_1+\beta_1,\alpha_2+\beta_2 \in {A+B}\)

那么则有 $(\alpha_1+\beta_1)x+(1-x)\ (\alpha_2+\beta_2) = \alpha_1x+(1-x)\alpha_2 + \beta_1x+(1-x)\beta_2 $

其中 \(\alpha_1x+(1-x)\alpha_2\in A\), \(\beta_1x+(1-x)\beta_2\in B\) ，那么就有 \((\alpha_1+\beta_1)x+(1-x)\ (\alpha_2+\beta_2)\in A+B\) ,所以闵可夫斯基和也是个凸集。

结论2：任意一条凸包 \(A\) 或 \(B\) 的边，那么一定也是 $A+B $ 的边。

证明：

一条线段在一个凸包上，等价于凸包上有一条线段和这一条线段的斜率相等，且线段外侧没有其他的点。

还是那刚才的图来举例：

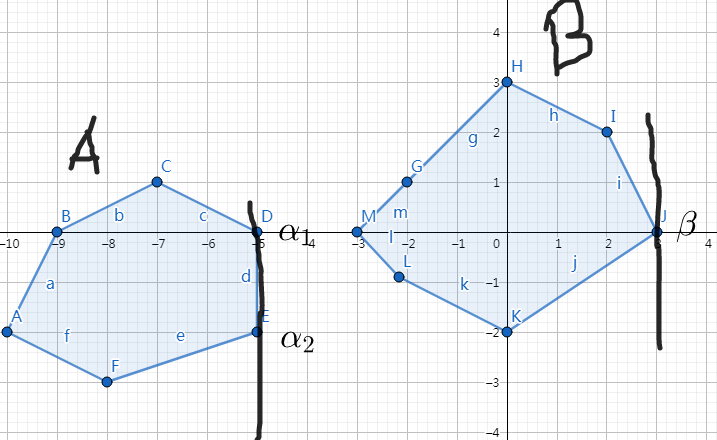
比如说我们确定 \(\alpha_1\alpha_2\) 这条边是否出现在 \(A+B\) 上，我们取 \(B\) 中离 \(\alpha_1 \alpha_2\) 这条边最远的一个切点 $ \beta$ ，那么显然 \(\alpha_1+\beta\) 和 \(\alpha_2+\beta\) 都属于 \(A+B\), 且 这一条线段的斜率等于 \(\alpha_1\alpha_2\) 的斜率，在这一条线段之外没有其他的点（因为 \(\alpha_1\alpha_2\) 是 凸包 $ A$ 这个方向的最大值， \(\beta\) 是凸包 \(B\) 这个方向的最大值，两个最大值相加肯定也是最大的） 。

闵可夫斯基和的求法:

假设我们有 \(n\) 个点的凸包 \(A\) 和 \(m\) 个点的凸包 \(B\), 我们把凸包 \(A\) 和 \(B\) 上的边表示出来也就是 \(\vec{A_iA_{i+1}}\) 和 \(\vec{B_iB_{i+1}}\) 根据结论 \(2\) 可得，这些边都是 \(A\) 和 \(B\) 的闵可夫斯基和上的边，现在我们就考虑怎么把这些边组成一个凸多边形。

首先，我们把每条边按斜率大小 \(O(n)\) 的排序，然后我们把这些边按排完序之后的顺序依次接起来，就可以得到闵可夫斯基和的形态。然后把 \(A\) 和 \(B\) 中横纵坐标的最小值相加，就可以确定出闵可夫斯基和的横纵坐标的最小值，显然这个凸包的形态就是唯一的。

void Minkowski()
{
	for(ll i=1;i<n;i++) s1[i]=C1[i+1]-C1[i];s1[n]=C1[1]-C1[n];
	for(ll i=1;i<m;i++) s2[i]=C2[i+1]-C2[i];s2[m]=C2[1]-C2[m];
	A[tot=1]=C1[1]+C2[1];
	ll p1=1,p2=1;
	while(p1<=n&&p2<=m) ++tot,A[tot]=A[tot-1]+(s1[p1]*s2[p2]>=0?s1[p1++]:s2[p2++]);
	while(p1<=n) ++tot,A[tot]=A[tot-1]+s1[p1++];
	while(p2<=m) ++tot,A[tot]=A[tot-1]+s2[p2++];
}

例题： JSOI2018战争

这个题让我们判断 \(A+\alpha\) 和 \(B\) 是否重合。

对于 \(A\) 中一个点 \(x\) 和 \(B\) 中一个点 \(y\), 那么 \(\alpha = y-x\)

则不合法的 $\alpha $ 的集合就是 \(C= \{y-x\},y\in B,x\in A\) 。

我们把 \(A\) 的坐标去相反数就变为了 \(B\) 和 \(A\) 的闵可夫斯基和。

每次询问判断一个点是否在这个凸包里面，二分即可。

pick定理

这个当公式记就好了，一般来说没什么用。

给定顶点均为整点的简单多边形，皮克指出了其面积 \(A\) 与内部格点数 \(i\) 和边上格点数 \(b\) 的关系： \(A= i + {b\over 2} - 1\)

具体证明：论文

高维中，皮克定理和欧拉公式 \(V - E + F = 2\) 是等价的. (\(V,E,F\) 表示简单几何体的顶点数，边数，面数)

例题：poj 1265

平面图转对偶图

简单来说，平面图就是点和点之间有连边的图，如图：

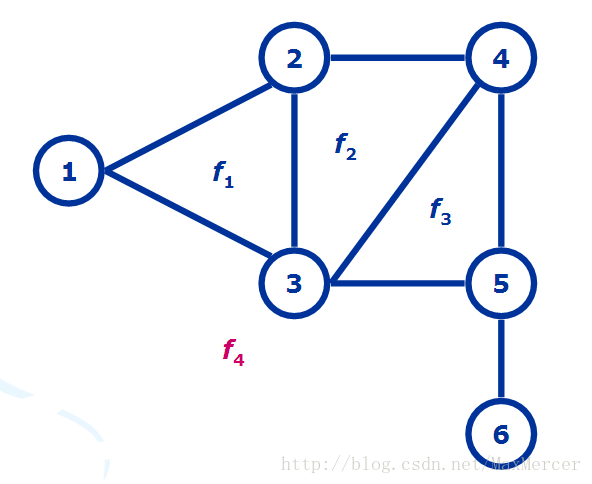
而他的对偶图呢，就是把每个面抠出来，标上号，如果两个面之间有交点，那么就在对偶图中连一条边。

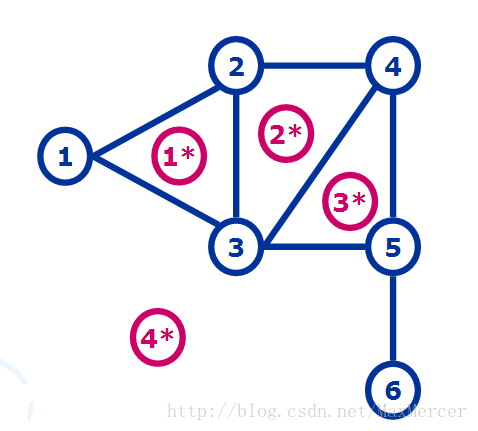
最后的对偶图建出来长这样：

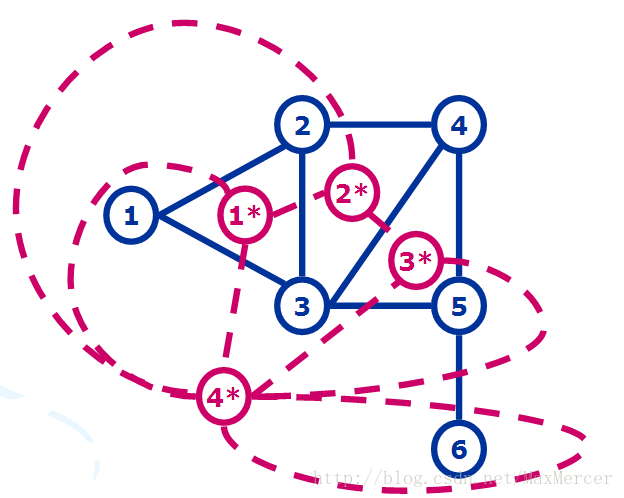
对偶图的性质：平面图的最小割等价于它对偶图的最短路。（这好像就不属于计算几何的内容了）。