AC自动机学习笔记
AC自动机:能自动AC的机器。
\(AC\) 自动机主要解决的是多模式串的匹配问题。
简单来说就是给你 \(n\) 个模式串 \(P_i\) 和文本串 \(T\), 问你 \(P_i\) 在 \(T\) 中出现了多少次。
有人会说,这不就是跑 \(n\) 遍 \(KMP\) 吗?效率很低,但 \(AC\) 自动机则可以较好的解决这个问题。
\(AC\) 自动机类似于 \(tire\) 树加 \(KMP\) 。构建 \(AC\) 自动机 一般来说有三个步骤:构建 \(tire\) 树,构建 \(fail\) 指针,匹配文本串。
下面我们举例子来挨个了解一下这几个步骤。
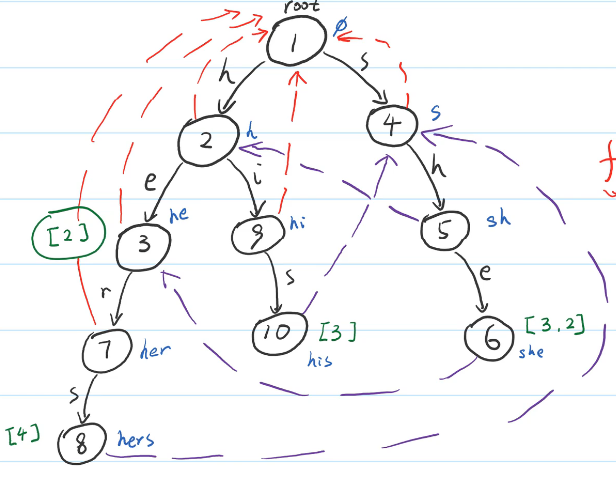
假设 P:{he,she,his,hers}, T: ahishers。
第一步:构建 \(tire\) 树
把所有的 \(P\) 串插入到一个 \(tir e\) 字典树当中。
那么上面的 \(P\) 串,插完之后如图:

第二步:构建 \(fail\) 指针
失配指针(\(fail\) 指针)是个什么东西捏?
设 \(word(i)\) 表示 \(tire\) 树上从根节点到 \(i\) 这个点所组成的字符串。如 \(word(3) = he\) .
如果说在 \(tire\) 树中, 如果 \(i\) 的失配指针为 \(j\), 那么 \(word(j)\) 是 \(word(i)\) 的最长公共后缀。
找 \(fail\) 指针也很简单,找到当前节点父亲的失配指针所指向的节点,看看这个节点是否有 \(c\) 这个字符,
如果有 \(c\) 的话,当前节点的 \(fail\) 指针就是这个节点,否则就往上跳 \(fail\) 指针,直到空节点。
怎么构造呢? 考虑 \(BFS\) 逐层构造。
首先第一层节点的 \(fai l\) 指针,肯定是 \(root\) 节点。
剩下的我们考虑字典树当前节点为 \(u\) ,他的父亲节点为 \(p\) , \(p\) 通过字符 \(c\) 的边指向 \(u\), 即: \(tr[p][c] = u\),
因为我们是逐层构造的,所以深度小于 \(u\) 的节点的 \(fail\) 节点已经求出来了。
1.如果 \(tr[p][c]\) 存在,则 \(tr[p][c]\) 的失配指针就是 \(p\) 的失配指针的 \(c\) 儿子,即:\(fail[tr[p][c]] = tr[fail[p]][c]\)
为什么呢?首先我们可以知道 \(word(fail[p])\) 是 \(P\) 的最长公共前缀,而 \(u\) 是由 \(p\) 加上一个字符 \(c\) 组成的。
那么 \(fail[p] + c\) 所组成的字符显然是 \(u\) 的最长公共后缀,也就是 \(fail[tr[p][c]] = tr[fail[p] ][c]\)。
\(tr[s][c]\) 相当于是在 \(s\) 后添加一个字符
c变成另一个状态 \(s'\), 由于 \(fail[s]\) 对应的字符串是 \(s\) 的后缀,因此 \(tr[s][c]\) 对应的字符串也是 \(s'\) 的后缀 -----by wiki。
2.如果 \(tr[p][c]\) 不存在的话,就让 \(tr[p][c]\) 指向 \(tr[fail[p]][c]\) 。
这个的意思就是说,\(tr[p][c]\) 指向的是 \(word(u)\) 出现在 \(tire\) 树中的最长后缀 (可以感性理解一下)。
这个方便我们在匹配的时候,可以直接跳到符合条件的节点。
上面的例子构造完失配指针后是这样的 :
我们可以模拟一下构建的过程 :
因为是bfs逐层遍历, 所以点的遍历顺序为1, 2, 4, 3, 9, 5, 7, 10, 6, 8
比如说遍历到2的时候, 当前字符串为h, 那么他没有后缀(严格来说是真后缀), 所以fail指向1(空节点).
再比如遍历到5的时候, 当前字符串为sh, 那么在这颗字典树中存在一个\(word[2]\)为h是sh的最长后缀, 所以fail指向2.
再再比如遍历到10的时候, 当前字符串为his, 那么在这颗字典树中存在一个\(word[4]\)为s是his的最长后缀, 所以fail指向4.不能错误的认为当前字符串的最长后缀为is, 因为这颗Tire树种不存在一个单词is;
一个动图:

然后我们就可以愉快的写代码了.
void Getfail()
{
queue<int> q;
for(int i = 0; i <= 26; i++)//根节点是0号点
{
if(!tr[root][i]) continue;//空节点的编号也是0号点,不能把空节点入队
fail[tr[root][i]] = root;
q.push(tr[root][i]);
}
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = 0; i <= 26; i++)
{
if(tr[x][i]) fail[tr[x][i]] = tr[fail[x]][i], q.push(tr[x][i]);//情况一
else tr[x][i] = tr[fail[x]][i];//情况二
}
}
}
通过上述的构造过程,我们可以得知, 从 \(u\) 这个节点一直跳 \(fail\) 指针,会得到一条 $fail $ 链,这条链上的任意一个节点 \(j\), 都满足 \(word(j)\) 是 \(word(u)\) 的后缀。
有了这个性质,我们就可以进行最后一步:文本串匹配。
第三步:匹配文本串
我们设 \(s[j]\) 表示从 \(1\) 到 \(j\) 所组成的字符串。
我们先枚举一下当前匹配到了文本串的位置 \(i\) , 那么出现次数发生变化的肯定是 \(s[i]\) 的后缀。
因此,我们可以在 \(tire\) 树上找到 \(s[i]\) 这个节点,然后不断跳 \(fail\) 指针,由上面的性质可知:这一条链上的点都是
\(s[i]\) 的后缀,然后对于这条链上的点 \(i\), \(word(i)\) 在文本串中出现的次数加一。
还是用上面的例子 : ahishers
开始从节点1出发, 发现没有一个子节点为'a', 于是走到节点1的fail指针所指向的节点, 还是1节点, 开始查找h;
从节点1出发, 发现有一个子节点为'h', 走到节点2, 但是节点2不存在P串, 所以并没有统计答案,开始查找i;
走到节点2, 发现有一个子节点为'i', 走到节点9, 还是不存在P串, 开始查找s;
走到节点9, 发现有一个子节点为's', 走到节点10, 存在P串his, 于是his的出现次数 + 1.
走到节点10, 发现没有一个子节点为'h', 所以走到节点10的fail指针所指向的节点4, 开始查找h;
走到节点4, 发现有一个子节点为'h', 走到节点5, 不存在能在P串, 开始查找e;
走到节点5, 发现有一个子节点为'e', 走到节点6, 存在P串she, 于是she的出现次数 + 1;
走到节点6, 发现没有一个子节点为'r', 所以走到节点6的fail指针所指向的节点3, 发现有一个P串he, 于是he的出现次数 + 1;
走到6节点, 发现有一个子节点为'r', 走到7节点, 不存在P串, 开始查找s;
走到7节点, 发现有一个子节点为's', 走到8节点, 存在P串hers, 于是hers的出现次数 + 1;
发现T串查找完了, 结束查找过程.
匹配代码:
int match(char *s)
{
int ans = 0;
int p = root, len = strlen(s);
for(int i = 0; i < len; i++)
{
int c = s[i] - 'a';
p = tr[p][c];//在tire树中找到 s[i] 节点
for(int x = p; x && end[x] != -1; x = fail[x]) ans += end[x], end[x] = -1;//不断跳fail指针。
}
return ans;
}
完整代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
int n,root,tot,tr[5000010][30],end[5000010],fail[5000010];
char s[5000010];
void insert(char *s)
{
int p = root, len = strlen(s);
for(int i = 0; i < len; i++)
{
int c = s[i] - 'a';
if(!tr[p][c]) tr[p][c] = ++tot;
p = tr[p][c];
}
end[p]++;//end[p]表示 word(p) 在模式串中出现的次数。
}
void Getfail()//构建fail指针
{
queue<int> q;
for(int i = 0; i <= 26; i++)
{
if(!tr[root][i]) continue;
fail[tr[root][i]] = root;
q.push(tr[root][i]);
}
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = 0; i <= 26; i++)
{
if(tr[x][i]) fail[tr[x][i]] = tr[fail[x]][i], q.push(tr[x][i]);
else tr[x][i] = tr[fail[x]][i];
}
}
}
int match(char *s)
{
int ans = 0;
int p = root, len = strlen(s);
for(int i = 0; i < len; i++)
{
int c = s[i] - 'a';
p = tr[p][c];//在tire树中找到 s[i] 这个节点
for(int x = p; x && end[x] != -1; x = fail[x]) ans += end[x], end[x] = -1;//不断跳fail指针
}
return ans;
}
int main()
{
scanf("%d",&n);
for(int i = 1; i <= n; i++)
{
cin>>s;
insert(s);
}
Getfail();
cin>>s;
printf("%d\n",match(s));
return 0;
}
一些优化
很简单就是一个 \(AC\) 自动机的板子题。但你交上去之后,你会发现你 T 成狗了。
这我们需要优化一下 匹配过程。
考虑一条 \(fail\) 链上虽然每个节点都是当前这个字符串的后缀,但每个节点的 \(word(i)\) 并不一定出现在模式串中。
所以考虑开个 \(last\) 数组,表示在这一条 \(fail\) 链上,上一次出现在模式串中的后缀是那个节点。
具体构造的时候只需要把 \(Getfail\) 函数改一下就好了:
void Getfail()
{
queue<int> q;
for(int i = 0; i <= 26; i++)
{
if(!tr[root][i]) continue;
fail[tr[root][i]] = root;
q.push(tr[root][i]);
}
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = 0; i <= 26; i++)
{
if(tr[x][i])
{
fail[tr[x][i]] = tr[fail[x]][i];//end[x] 表示word(x) 是否在模式串中出现过。
last[tr[x][i]] = end[fail[tr[x][i]]] ? fail[tr[x][i]] : last[fail[tr[x][i]]];//顺便维护一下last数组
q.push(tr[x][i]);
}
else tr[x][i] = tr[fail[x]][i];
}
}
}
最后例题的完整代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int N = 2e6+10;
int n,root,tot,tr[N][30],ans[N],fail[N],end[N],last[N];
string s,t;
vector<int> v[N];
void insert(string s,int id)
{
int p = root, len = s.length();
for(int i = 0; i < len; i++)
{
int c = s[i] - 'a';
if(!tr[p][c]) tr[p][c] = ++tot;
p = tr[p][c];
}
v[p].push_back(id);
end[p] = 1;
}
void Getfail()
{
queue<int> q;
for(int i = 0; i <= 26; i++)
{
if(!tr[root][i]) continue;
fail[tr[root][i]] = root;
q.push(tr[root][i]);
}
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = 0; i <= 26; i++)
{
if(tr[x][i])
{
fail[tr[x][i]] = tr[fail[x]][i];
last[tr[x][i]] = end[fail[tr[x][i]]] ? fail[tr[x][i]] : last[fail[tr[x][i]]];
q.push(tr[x][i]);
}
else tr[x][i] = tr[fail[x]][i];
}
}
}
void match(string s)
{
int p = root, len = s.length();
for(int i = 0; i < len; i++)
{
int c = s[i] - 'a';
p = tr[p][c];
for(int x = p; x; x = last[x])
{
for(int j = 0; j < v[x].size(); j++) ans[v[x][j]]++;
}
}
}
int main()
{
scanf("%d",&n);
for(int i = 1; i <= n; i++)
{
cin>>s;
insert(s,i);
t += s;
t += '#';
}
Getfail();
match(t);
for(int i = 1; i <= n; i++) printf("%d\n",ans[i]);
return 0;
}
然后因为 \(AC\) 自动机它是一棵类似于树一样的东西。
所以我们可以根据这个来搞一些奇奇怪怪的操作:AC自动机上 dp,AC自动机套线段树合并。
然后这就属于我这种小蒟蒻能够做出来的题了。



