多项式学习笔记(一) FFT
1.多项式
定义 \(F(x)\) 表示一个 \(n-1\) 次的多项式(其实你可以把多项式理解为方程)。
则 \(F(x) = a_0x^0 + a_1x^1 + a_2x^2+...a_{n-1}x^{n-1}\) ,即 \(F(x) =\displaystyle\sum_{i=0}^{n-1}a^ix^i\)。
这也就是我们经常用的系数表示法(初中应该都学过吧)。
2.点值表示法
在介绍 \(FFT\) 之前,有必要接触一下这种方法。
首先我们可以知道 \(n\) 个点可以确定一个 \(n-1\) 次的多项式,因为你可以通过各种消元得到每一次的系数。
如 \(F(x) = x^2+3x+1\) . 我们就可以用点值表示法表示为 \((0,1),(1,5),(-1,-1)\).
3.多项式乘法
其实多项式乘法就是卷积的形式。
假如我们有两个多项式 \(A(x)\) 和 \(B(x)\), 其中 \(A(x) = a_0x^0+a_1x^1+a_2x^2....a_{n-1}x^{n-1}\), \(B(x) = b_0x^0+b_1x^1+b_2x^2....b_{m-1}x^{m-1}\)
显然如果 \(A(x) \times B(x) = C(x)\) ,那么 \(C_i = \displaystyle\sum_{i=0}^{i}a_ib_{i-j}\).
这样直接乘的复杂度是 \(O(n^2)\) 的,下面要讲的 \(FFT\) 则可以使他变为 \(O(nlogn)\)。
4.FFT
这个就是我们今天的主角,它的全称叫 快速离散傅里叶变化,据说傅里叶大神在计算机发明的100多年前就发明了这个算法。
下面我们来看看他是具体怎么操作的。
假如说我们已经知道了 \(A(x)\) 和 \(B(x)\) 在 \(x_0\) 处的取值,那么 \(C(x)\) 在 \(x_0\) 处的取值直接把两个数相乘就可以得到。
间接地我们就知道了 \(C(x)\) 的点值表示法。
来后整个 \(FFT\) 的流程我们就大致知道了:
- 求值,分别求出多项式 \(A(x),B(x)\) 的点值表示法
- 相乘,把 \(A(x),B(x)\) 的点值乘起来,得到 \(C(x)\) 的点值表示法 。
- 插值,把 \(C(x)\) 的点值表示法转化为系数表示法。
中间第二部相乘,显然可以做到 \(O(n)\) 的来写。第一步朴素算法就是找 \(n\) 个不同的值分别代入方程中,复杂度为 \(O(n^2)\) 的,第三部复杂度就更槽糕了,直接高斯消元的话复杂度直接变为 \(O(n^3)\) 的,这比直接相乘的暴力还要慢,显然还需要继续优化。
运用点值表示法,我们可以任意选 \(n\) 个数代进去,这启发我们从这里入手开始优化,那么傅里叶大神也注意到了这一点,把复数和单位根引进了这个方程中。
5.单位根及其性质
在了解把复数和单位根引入这个方程有什么用前,要先了解一下,单位根的性质。
首先,单位根所在的点就是把单位圆平均分为 \(n\) 份的分割点,也就是一个向量。
我们一般从 \((0,1)\) 开始逆时针开始标号得到 \(w_{n}^{0},w_{n}^{1}...w_{n}^{n-1}\),,
例如八次单位根
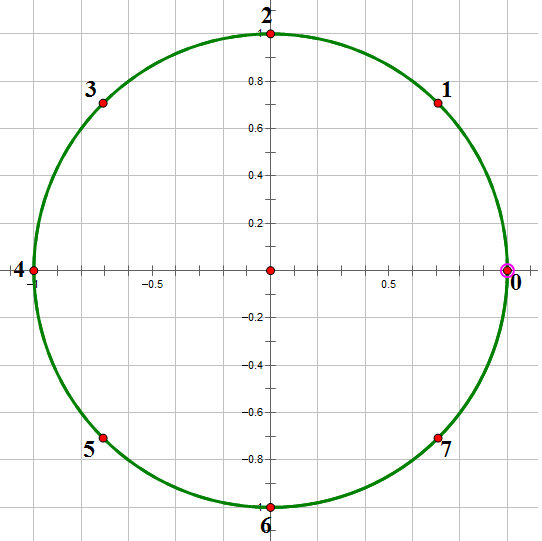
单位根有如下几条性质:
性质1: \(w_{n}^{k} = (w_{n}^{1})^k\)
证明:
\(w_{n}^{k} \times w_{n}^{1} = (\cos{k\over n}2π,\sin{n\over k}2π) * (\cos{1\over n}2π,\sin{1\over n}2π)\)
\(=(\cos{k\over n}2π\times \cos{1\over n}2π-\sin{n\over k}2π\times \sin{1\over n} 2π,\cos{k\over n}2π\times \sin{1\over n}2π-\sin{k\over n}2π\times cos{1\over n}2π\)
\(=(\cos({k\over n}+{1\over n})2π,\sin({k\over n}+{1\over n})2π)\)
\(=(\cos{{k+1}\over n}2π,\sin{{k+1}\over n}2π)\)
\(= w_{n}^{k+1}\)
至于第二步怎么转化过来的,具体可以看一下 和角公式 。
性质2: \((w_{n}^{x})^{y} = w_{n}^{x*y}\)
证明:
首先我们有 \((a^x)^y = a^{x*y}\) ,
然后就有 \((w_{n}^{x})^y = ((w_n^{1})^x)^y = (w_{n}^{1})^{x*y} = w_{n}^{x*y}\).
性质3: \(w_{n*x}^{k*x} = w_{n}^{k}\)
证明:
\(w_{n*x}^{k*x} = (\cos{k*x\over{n*x}}2π,\sin{k*x\over{n*x}}2π)\)
\(=\cos_{n}^{k}2π,\sin_{n}^{k}2π\) (约分大法好)
\(=w_{n}^{k}\)
性质4: 如果 \(n\) 为偶数,则 \(w_{n}^{k} = -w_{n}^{k+{n\over 2}}\)
证明:
你观察一下上面的那个图就会发现, \(w_n^{k+{n\over 2}}\) 所表示的向量其实是 \(w_n^{k}\) 这个向量旋转 180 度之后得到的。
然后仔细观察一下他们好像关于原点对称,那么自然满足 \(w_{n}^{k} = -w_{n}^{k+{n\over 2}}\).
数学证明:
\(-w_{n}^{k+{n\over 2}} = -(\cos({k+{n\over 2}\over n})2π,\sin({{k+{n\over 2}}\over {n}}2π)\)
\(=-(-\cos{k\over n}2π,-\sin{k\over n}2π)\)
\(=(cos({k\over n}2π,\sin{k\over n}2π)\)
$=w_{n}^{k} $
诱导公式nb, \(\cos(x+π) = -\cos x\), \(sin(x+π) = -sin(x+π)\)。
6.插值优化
既然单位根有那么多的性质,那么把他代入方程会产生神马化学反应呢?
第一点就是比较方便插值。
首先 \(F(x)\) 的离散傅里叶变换指把 \(w_n^{0},w_{n}^{1}....w_{n}^{n-1}\) 作为多项式(方程)的 \(x\) 代入得到 \((y_0,y_1...y_{n-1})\) ,实际上他是一个插值的过程。
然后现在有一个结论:
对一个多项式进行离散傅里叶变换得到的 \((y_0,y_1...y_{n-1})\) 作为系数组成一个新的多项式 \(B(x)\),然后把 \(n\) 个单位根 \(w_n^{0},w_{n}^{1}....w_{n}^{n-1}\) 取倒数代入得到 \((z_0,z_1....z_{n-1})\) , 那么 \(A(x)\) 第 \(i\) 项的系数就是 \(z_{i}\) 除以 \(n\) 的结果。
具体来说就是:
\(A(x) = a_0x^0+a_1x^1+a_2x^2...a_{n-1}x^{n-1}\)
将 \(w_n^{0},w_{n}^{1}....w_{n}^{n-1}\) 分别作为 \(x\) 代入求值得到 \((y_0,y_1...y_{n-1})\)
\(B(x) = y_0x^0 + y_1x^1+y_2x^2+y_{n-1}x^{n-1}\)
然后再把 \((w_{n}^{-1},w_{n}^{-2}...w_{n}^{-(n-1)})\) 作为 \(x\) 代入求值,得到 \((z_0,z_1.....z_{n-1})\)
最后 \(z_k = a_{k}*n\)
证明:
\(z_k = \displaystyle\sum_{i=0}^{n-1}y_i * (w_{n}^{-k})^i\)
\(=\displaystyle\sum_{i=0}^{n-1}(w_{n}^{-k})^i(\sum_{j=0}^{n-1}a_j * (w_{n}^{i})^j )\)
\(=\displaystyle\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j*(w_{n}^{i})^j * (w_{n}^{-k})^i\)
\(=\displaystyle\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j*w_n^{i*j} * w_n^{-k*i}\)
\(=\displaystyle\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j*w_{n}^{i*(j-k)}\)
\(=\displaystyle\sum_{j=0}^{n-1}a_j \sum_{i=0}^{n-1}(w_n^{j-k})^i\)
对于 \(\displaystyle\sum_{i=0}^{n-1}(w_n^{j-k})^i\) 我们发现,当 \(j ==k\) 的时候,这个值等于 \(n\) .
其他情况下这个值都为 \(0\) ,这个需要用等比序列求和来做。
首先,把求和项展开可以发现是一个公比为 \(w_n^{j-k}\) 的一个等比序列,利用求和公式可得:
\(\displaystyle\sum_{i=0}^{n-1}(w_n^{j-k})^i = {(w_{n}^{j-k})^n -1\over w_{n}^{j-k}-1} = {(w_{n}^{n})^{j-k}-1\over w_n^{j-k}-1} = {1^{j-k}-1\over w_n^{j-k}-1} = 0\)
因此 \(z_k = a_k * n\).
所以,我们利用离散傅里叶变换,把插值就变为了一次求值的过程,现在主要是解决求值的问题。
7.求值优化
首先我们定义一个多项式 \(A(x) = a_0x^0+a^1x^1+a^2x^2....a_{n-1}x^{n-1}\), 然后要求的是把 \(w_{n}^{0},w_{n}^{1}....w_{n}^{n-1}\) 代入后的结果。
这个到底怎么做的,我们现在引进快速傅里叶变换。
它主要把次数按奇偶项分类进行处理。
比如: \(A(x) = (a_0x^0+a_2x^{2}+a_4x^4.....) + (a_1x^1+a_3x^3+a^5x^5......)\)
设 \(A1(x) = a_0x^0+a^2x^1+a_4x^2.....\) , \(A2(x) = a_1x^0+a_3x^1+a_5x^2...\)
显然 \(A(x) = A1(x^2) + xA2(x^2)\)
然后我们尝试把单位根代入
如果 \(这个值 < {n\over 2}\) ,我们直接把 \(k\) 代入得:
\(A(w_n^{k}) = A1(w_n^{2k}) + w_n^{k}A2(w_n^{2k}) = A1(w_{n\over 2}^{k}) + w_{n}^{k}A2(w_{n\over 2}^{k}))\)
如果 $这个值\geq {n\over 2} $,我们把 \(w_{n}^{k+{n\over 2}}\) 代入可得:
\(A(w_{n}^{k+{n\over 2}}) = A1(w_{n}^{2k+n})+w_{n}^{k+{n\over 2}}A2(w_{n}^{2k+n}) = A1(w_{n}^{2k}*w_{n}^{n}) - w_{n}^{k}A2(w_{n}^{2k}*w_{n}^{n}) = A1(w_{n\over 2}^{k})-w_{n}^{k}A2(w_{n\over 2}^k)\)
假如你知道 \(A1(x)\) 和 \(A2(x)\) 代入 \(w_{n\over 2}^{0},w_{n\over 2}^{1}....w_{n\over 2}^{{n\over 2}-1}\) 的结果,那么 \(A(x)\) 代入 \(w_{n}^{0},w_{n}^1....w_{n}^{n-1}\) 的值我们就可以 \(O(n)\) 的得出来了。
我们可以一直递归下去,直到 \(n=0\) 时,柿子的值就是 \(w_n^0 \times 系数\) ,就可以直接 \(return\) 了。
复杂度 \(T(n) = 2*T({n\over 2})+O(n) = nlog n\)
下面给出 FFT 递归的实现版本
void FFT(complex *a,int len,int flag)
{
if(len == 1) return;//只有一次项的时候停止递归
int A1[N],A2[N];
for(int i = 0; i < len; i += 2)//按奇偶的奇偶分类递归
{
A1[i>>1] = a[i];
A2[i>>1] = a[i+1];
}
FFT(A1,len>>1,flag); FFT(A2,len>>1,flag);//递归计算 A1(x),A2(x)
complex wn = {cos(Pi/len),flag * sin(Pi/len)};//单位根
for(int i = 0; i < len>>1; i++)
{
complex u = A1[i];
complex v = w * A2[i];
a[i] = u + v;
a[i+(len>>1)] = u-v;
w = w * wn;//下一个单位根
}
}
8.递归转迭代
上面那么伪代码是不可以通过模板的,主要是递归的时候计算耗费了大量的常数。
一个比较好的优化方法就是递归转迭代。
有位大神发现 FFT 递归的时候有个性质,就是对于 \(a_x\) 他最后的位置就是把 \(x\) 的二进制位翻转的位置。
比如 \(4(100)->2(001)\) ,可以结合图理解一下:

这样我们可以 \(O(n)\) 的预处理处每个 \(ax\) 最后的系数,然后就可以借助非递归快速实现了。
总代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 5e6+10;
const double Pi = acos(-1.0);
int n,m,len,tim,Rev[N];
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
return s * w;
}
struct complex//定义一个复数
{
double x,y;
// complex(double a,double b){x = a, y = b;}
}a[N],b[N];
complex operator + (complex a, complex b){return (complex){a.x+b.x,a.y+b.y};}//重载复数的各种操作
complex operator - (complex a, complex b){return (complex){a.x-b.x,a.y-b.y};}
complex operator * (complex a, complex b){return (complex){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
void FFT(complex *a,int flag)
{
for(int i = 0; i < len; i++)
{
if(i < Rev[i]) swap(a[i],a[Rev[i]]);
}
for(int h = 1; h < len; h <<= 1)//从下往上开始合并,枚举这次合并的区间长度的一半是多少
{
complex wn = complex{cos(Pi/h),flag*sin(Pi/h)};//单位根
for(int j = 0; j < len; j += (h<<1))//枚举这一层每一组的起始位置
{
complex w = complex{1,0};
for(int k = 0; k < h; k++)//处理每一组的值
{
complex x = a[j+k];
complex t = w * a[j+k+h];
a[j+k] = x+t;
a[j+k+h] = x-t;
w = w * wn;
}
}
}
}
int main()
{
n = read(); m = read();
for(int i = 0; i <= n; i++) a[i].x = read();
for(int i = 0; i <= m; i++) b[i].x = read();
len = 1, tim = 0;
while(len <= n+m) len <<= 1, tim++;
for(int i = 0; i < len; i++) Rev[i] = (Rev[i>>1]>>1) | ((i&1)<<(tim-1));//预处理每个系数最后的位置,只可意会不可言传
FFT(a,1); FFT(b,1);
for(int i = 0; i < len; i++) a[i] = a[i] * b[i];
FFT(a,-1);
for(int i = 0; i <= n+m; i++) printf("%d ",(int) (a[i].x/len+0.5));
printf("\n");
return 0;
}

