线段树合并从入门到入土

前置知识：

动态开点线段树
权值线段树

如果你上面那两个不会的话，出门右转模板区。

线段树合并是什么东东呢？

他其实就是把好几个零散的线段树合并在一起。

就相当于重新开一颗权值线段树保存原来两棵线段树的信息。

他一般可以用来解决一些平衡树能做的题比如第\(k\) 大，排名，找前驱后继。

大体的实现思路：

若 \(x,y\) 一个为空节点，则以非空的最为合并之后的节点。
若 \(x,y\) 都不为空，则递归合并左右子树，以 \(x\) 作为合并之后的节点，并自下而上合并子树的信息

思想理解了的话，代码就不难实现了。

在这里 \(genshy\) 给大家提供两种不同的写法（自认为比较方便）。

1.合并区间最大值

这个时候我们还需要添两个参数记录一下区间的左右端点。毕竟叶子节点和非叶子节点的合并方式是不太一样的。

叶子节点的话直接把 \(x,y\) 两个值相加就可以，非叶子节点的话就可以由下面子树 \(up\) 上来

Code

void merage(int &x,int y,int l,int r)
{
	if(!x) {x = y; return;}//非空节点
	if(!y) return;
	int mid = (l + r)>>1;
	if(l == r) //叶子节点直接把权值相加
	{
		tr[x].sum += tr[y].sum;
		return;
	}
	merage(tr[x].lc,tr[y].lc,l,mid);//递归合并左右子树
	merage(tr[x].rc,tr[y].rc,mid+1,r);
	up(x);//up一下
}

2.合并区间和

这种类型我们就可以少传记录区间端点的两个参数，直接把 \(x,y\) 两个节点的值相加就完事了。

Code

void merage(int &x,int y)
{
 if(!x) {x = y; return;}
 if(!y) return;
 tr[x].sum += tr[y].sum;
 merage(tr[x].lc,tr[y].lc);
 merage(tr[x].rc,tr[y].rc);
}

一张很透彻的图像：

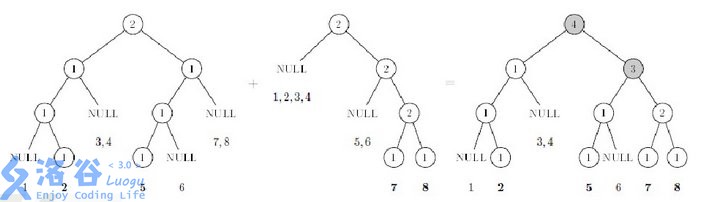
复杂度证明：

具体的我不太会证，所以直接把日报上的搬过来了。

先来思考一下在动态开点线段树中插入一个点会加入多少个新的节点
线段树从顶端到任意一个叶子结点之间有 \(logn\) 层，每层最多新增一个节点
所以插入一个新的点复杂度是 \(logn\) 的

两棵线段树合并的复杂度显然取决于两棵线段树重合的叶子节点个数，假设有 \(m\) 个重合的点，这两棵线段树合并的复杂度就是 \(mlogn\) 了，所以说，如果要合并两棵满满的线段树，这个复杂度绝对是远大于 \(logn\) 级别的。
也就是说，千万不要以为线段树合并对于任何情况都是 \(logn\) 的！

那么为什么数据范围 \(10^5\) 的题目线段树合并还稳得一批？
这是因为 \(logn\) 的复杂度仅适用于插入点少的情况。
如果 \(n\) 与加入的总点数规模基本相同，我们就可以把它理解成每次操作 \(O(logn)\)

来证明一下：
假设我们会加入 \(k\) 个点，由上面的结论，我们可以推出最多要新增 \(klogk\) 个点。
而正如我们所知，每次合并两棵线段树同位置的点，就会少掉一个点，复杂度为 \(O(1)\)，总共 \(klogk\)个点，全部合并的复杂度就是 \(O(klogk)\)

可见，上面那个证明是只与插入点个数 \(k\) 有关，也就是插入次数在\(10^5\)左右、值域 \(10^5\)左右的题目，线段树合并还是比较稳的。

下面我们就来看几道例题吧QAQ。

P3605 [USACO17JAN]Promotion Counting P

比较板的题了。

对于每个节点都开一个权值线段树，dfs的时候往上合并一下子树的信息。

点 \(x\) 答案就是 \([a[x]+1,n]\) 的区间和。

注意要离散化一下，数组尽量开大点。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int n,tot,u,cnt;
int head[N],rt[N],a[N],b[N],ans[N];
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s * w;
}
struct node
{
	int to,net;
}e[N<<1];
struct Tree
{
	int lc,rc,sum;
}tr[N*20];
void add(int x,int y)
{
	e[++tot].to = y;
	e[tot].net = head[x];
	head[x] = tot;
}
void insert(int &p,int l,int r,int x,int val)//动态开点
{
	if(!p) p = ++cnt;
	tr[p].sum += val;
	int mid = (l + r)>>1;
	if(l == r) return;
	if(x <= mid) insert(tr[p].lc,l,mid,x,val);
	if(x > mid) insert(tr[p].rc,mid+1,r,x,val);
	tr[p].sum = tr[tr[p].lc].sum + tr[tr[p].rc].sum;
}
int query(int o,int l,int r,int L,int R)
{
	int res = 0;
	if(!o) return 0;
	if(L <= l && R >= r) return tr[o].sum;
	int mid = (l + r)>>1;
	if(L <= mid) res += query(tr[o].lc,l,mid,L,R);
	if(R > mid) res += query(tr[o].rc,mid+1,r,L,R);
	return res;
}
void merage(int &x,int y)
{
	if(!x) {x = y; return;}
	if(!y) return;
	tr[x].sum += tr[y].sum;
	merage(tr[x].lc,tr[y].lc);
	merage(tr[x].rc,tr[y].rc);
}
void dfs(int x,int fa)
{
	insert(rt[x],1,n,a[x],1);
	for(int i = head[x]; i; i = e[i].net)
	{
		int to = e[i].to;
		if(to == fa) continue;
		dfs(to,x);
		merage(rt[x],rt[to]);//合并一下
	}
	ans[x] = query(rt[x],1,n,a[x]+1,n);//统计一下答案
}
int main()
{
	n = read();
	for(int i = 1; i <= n; i++) a[i] = b[i] = read();
	sort(b+1,b+n+1);
	int num = unique(b+1,b+n+1)-b-1;
	for(int i = 1; i <= n; i++) a[i] = lower_bound(b+1,b+num+1,a[i])-b;//离散化
	for(int i = 2; i <= n; i++)
	{
		u = read();
		add(u,i); add(i,u);
	}
	dfs(1,1);//dfs统计答案
	for(int i = 1; i <= n; i++) printf("%d\n",ans[i]);
	return 0;
}

P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并

真正的模板题来了。

考虑对每种粮食树上差分一下， \(d[x]+1,d[y]+1,d[lca]-1,d[fa[lca]]-1\)，随便拿线段树维护一下这些差分数组。

最后在 \(dfs\) 一下统计每个点的答案，顺便把儿子节点的线段树和父亲节点合并一下。

然后这道题就做完了。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int lim = 1e5;
const int N = 3e5+10;
int n,m,tot,cnt,x,y,z,u,v;
int head[N],dep[N],fa[N],siz[N],son[N],top[N],rt[N],ans[N];
struct node
{
	int to,net;
}e[N<<1];
struct Tree
{
	int lc,rc;
	int sum,id;
}tr[N<<4];
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s * w;
}
void add(int x,int y)
{
	e[++cnt].to = y;
	e[cnt].net = head[x];
	head[x] = cnt;
}
void get_tree(int x)//树剖求lca
{
	dep[x] = dep[fa[x]] + 1; siz[x] = 1;
	for(int i = head[x]; i; i = e[i].net)
	{
		int to = e[i].to;
		if(to == fa[x]) continue;
		fa[to] = x;
		get_tree(to);
		siz[x] += siz[to];
		if(siz[to] > siz[son[x]]) son[x] = to;
	}
}
void dfs(int x,int topp)
{
	top[x] = topp;
	if(son[x]) dfs(son[x],topp);
	for(int i = head[x]; i; i = e[i].net)
	{
		int to = e[i].to;
		if(to == fa[x] || to == son[x]) continue;
		dfs(to,to);
	}
}
int lca(int x,int y)
{
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		x = fa[top[x]];
	}
	return dep[x] <= dep[y] ? x : y;
}
void up(int p)
{
	tr[p].sum = max(tr[tr[p].lc].sum,tr[tr[p].rc].sum);
	tr[p].id = tr[p].sum == tr[tr[p].lc].sum ? tr[tr[p].lc].id : tr[tr[p].rc].id;
}
void insert(int &p,int l,int r,int x,int val)
{
	if(!p) p = ++tot;
	if(l == r)
	{
		tr[p].sum += val;
		tr[p].id = x;
		return;
	}
	int mid = (l + r)>>1;
	if(x <= mid) insert(tr[p].lc,l,mid,x,val);
	if(x > mid) insert(tr[p].rc,mid+1,r,x,val);
	up(p);
}
pair<int,int> query(int o,int l,int r,int L,int R)
{
	int ans = 0, id = 0;
	if(!o) return make_pair(0,0);
	if(L <= l && R >= r)
	{
		if(tr[o].sum == 0) return make_pair(0,0);
		else return make_pair(tr[o].sum,tr[o].id);
	}
	int mid = (l + r)>>1;
	if(L <= mid) 
	{
		pair<int,int> kk = query(tr[o].lc,l,mid,L,R);
		if(ans < kk.first)
		{
			ans = kk.first;
			id = kk.second;
		}
	}
	if(R > mid)
	{
		pair<int,int> kk = query(tr[o].rc,mid+1,r,L,R);
		if(ans < kk.first)
		{
			ans = kk.first;
			id = kk.second;
		}
	}
	return make_pair(ans,id);
}
void merage(int &x,int y,int l,int r)
{
	if(!x) {x = y; return;}
	if(!y) return;
	int mid = (l + r)>>1;
	if(l == r) 
	{
		tr[x].sum += tr[y].sum;
		return;
	}
	merage(tr[x].lc,tr[y].lc,l,mid);
	merage(tr[x].rc,tr[y].rc,mid+1,r);
	up(x);
}
void get_ans(int x,int fa)
{
	for(int i = head[x]; i; i = e[i].net)
	{
		int to = e[i].to;
		if(to == fa) continue;
		get_ans(to,x);
		merage(rt[x],rt[to],1,lim);//合并儿子节点
	}
	pair<int,int> kk = query(rt[x],1,lim,1,lim);
	ans[x] = kk.second;
}
int main()
{
	n = read(); m = read();
	for(int i = 1; i <= n-1; i++)
	{
		u = read(); v = read();
		add(u,v); add(v,u);
	}
	get_tree(1); dfs(1,1);
	for(int i = 1; i <= m; i++)
	{
		x = read(); y = read(); z = read();
		int Lca = lca(x,y);
		insert(rt[x],1,lim,z,1);//树上差分
		insert(rt[y],1,lim,z,1);
		insert(rt[Lca],1,lim,z,-1);
		insert(rt[fa[Lca]],1,lim,z,-1);
	}
	get_ans(1,1);//统计答案
	for(int i = 1; i <= n; i++) printf("%d\n",ans[i]);
	return 0;
}

P3224 [HNOI2012]永无乡

板子题。

对于每个联通块都开个权值线段树。并查集维护这些块的连通性。

并查集合并的时候，顺便把这两个联通块的线段树合并一下。

注意并查集合并的方向要和线段树合并的方向相同。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int n,m,q,u,v,tot,x,y;
int p[N],fa[N],rt[N];
struct Tree
{
	int lc,rc,sum,id;
}tr[N*20];
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s * w;
}
int find(int x)
{
	if(fa[x] == x) return x;
	else return fa[x] = find(fa[x]);
}
void insert(int &p,int l,int r,int x,int val,int id)
{
	if(!p) p = ++tot;	
	tr[p].sum += val;
	if(l == r) {tr[p].id = id; return;}
	int mid = (l + r)>>1;
	if(x <= mid) insert(tr[p].lc,l,mid,x,val,id);
	if(x > mid) insert(tr[p].rc,mid+1,r,x,val,id);
	tr[p].sum = tr[tr[p].lc].sum + tr[tr[p].rc].sum;
}
int query(int o,int l,int r,int k)//线段树二分求区间第k大
{
	if(l == r) return tr[o].id;
	if(!o) return -1;
	int mid = (l + r)>>1;
	if(tr[tr[o].lc].sum >= k) return query(tr[o].lc,l,mid,k);
	else return query(tr[o].rc,mid+1,r,k-tr[tr[o].lc].sum);
}
void merage(int &x,int y)
{
	if(!x){x = y; return;}
	if(!y) return;
	tr[x].sum += tr[y].sum;
	tr[x].id += tr[y].id;
	merage(tr[x].lc,tr[y].lc);
	merage(tr[x].rc,tr[y].rc);
}
int main()
{
	n = read(); m = read();
	for(int i = 1; i <= n; i++)
	{
		p[i] = read();
		insert(rt[i],1,n+1,p[i],1,i);
	}
	for(int i = 1; i <= n; i++) fa[i] = i;
	for(int i = 1; i <= m; i++)
	{
		u = read(); v = read();
		int fx = find(u);
		int fy = find(v);
		if(fx == fy) continue;
		fa[fy] = fx;//并查集合并的方向要和线段树合并的方向相同
		merage(rt[fx],rt[fy]);//合并两个联通块的线段树
	}
	q = read();
	for(int i = 1; i <= q; i++)
	{
		char ch; cin>>ch;
		x = read(); y = read();
		if(ch == 'Q')
		{
			int fx = find(x);
			int ans = query(rt[fx],1,n+1,y);
			printf("%d\n",ans == n+1 ? -1 : ans);
		}
		else
		{
			int fx = find(x);
			int fy = find(y);
			if(fx == fy) continue;
			fa[fy] = fx;
			merage(rt[fx],rt[fy]);//合并
		}
	}
	return 0;
}

P4197 Peaks

这题需要好好的想一想。

好像听别的巨佬说这似乎是克鲁斯卡尔重构树的板子题，但我太菜了，没学会。

所以只能拿点简单的做法水一下了。

考虑没有边权的情况就和上面永无乡那道题是一样的题。

有了边权处理起来就比较麻烦。

我们可以考虑对询问离线一下。

从困难值小的开始处理，每次把边权比困难值小的边加进去合并一下。

还是和上面那个题一样的思路并查集维护联通块连通性，线段树维护每个联通块的信息。

并查集合并的时候顺便把线段树也合并一下，然后这题就做完了。

一个要注意的点就是在同一联通块之间的线段树不要合并，否则复杂度会退化到 \(O(n^2)\) 的。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int n,m,cntq,tot,last = 1;
int h[N],rt[N],fa[N],b[N],ans[500010];
struct bian
{
	int u,v,w;
}e[500010];
struct node
{
	int x,v,k,id;
}q[500010];
struct Tree
{
	int lc,rc,sum;
}tr[N*20];
bool comp(bian a,bian b){ return a.w < b.w;}
bool cmp(node a,node b){ return a.v < b.v; }
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s * w;
}
int find(int x)
{
	if(fa[x] == x) return x;
	else return fa[x] = find(fa[x]);
}
void insert(int &p,int l,int r,int x,int val)
{
	if(!p) p = ++tot;
	tr[p].sum += val;
	if(l == r) return;
	int mid = (l + r)>>1;
	if(x <= mid) insert(tr[p].lc,l,mid,x,val);
	if(x > mid) insert(tr[p].rc,mid+1,r,x,val);
	tr[p].sum = tr[tr[p].lc].sum + tr[tr[p].rc].sum;
}
int query(int o,int l,int r,int k)//线段树二分求区间第k大，优先递归右子树
{
	if(l == r) return l;
	if(tr[o].sum < k) return -1;
	int mid = (l + r)>>1;
	if(tr[tr[o].rc].sum >= k) return query(tr[o].rc,mid+1,r,k);
	else return query(tr[o].lc,l,mid,k-tr[tr[o].rc].sum);
}
void merage(int &x,int y)
{
	if(!x){x = y; return;}
	if(!y) return;
	tr[x].sum += tr[y].sum;
	merage(tr[x].lc,tr[y].lc);
	merage(tr[x].rc,tr[y].rc);
}
int main()
{
	n = read(); m = read(); cntq = read();
	for(int i = 1; i <= n; i++) b[i] = h[i] = read();
	sort(b+1,b+n+1);
	int num = unique(b+1,b+n+1)-b-1;
	for(int i = 1; i <= n; i++) fa[i] = i;
	for(int i = 1; i <= n; i++) h[i] = lower_bound(b+1,b+num+1,h[i])-b;
	for(int i = 1; i <= m; i++)
	{
		e[i].u = read();
		e[i].v = read();
		e[i].w = read();
	}
	sort(e+1,e+m+1,comp);
	for(int i = 1; i <= cntq; i++)
	{
		q[i].x = read();
		q[i].v = read();
		q[i].k = read();
		q[i].id = i;
	}
	sort(q+1,q+cntq+1,cmp);//离线一下
	for(int i = 1; i <= n; i++)
	{
		insert(rt[i],1,n,h[i],1);
	}
	for(int i = 1; i <= cntq; i++)
	{
		while(last <= m && e[last].w <= q[i].v)
		{
			int fx = find(e[last].u);
			int fy = find(e[last].v);
			if(fx == fy){ last++; continue;}
			fa[fy] = fx;
			merage(rt[fx],rt[fy]);//线段树并查集合并
			last++;
		} 
		int fx = find(q[i].x);
		int res = query(rt[fx],1,n,q[i].k);
		ans[q[i].id] = res == -1 ? -1 : b[res];
	}
	for(int i = 1; i <= cntq; i++) printf("%d\n",ans[i]);
	return 0;
}

课后练习题：

1.CF1009F Dominant Indices 线段树合并优化dp

2.CF490F Treeland Tour 线段树合并优化dp

posted @ 2020-10-09 21:43 genshy 阅读(340) 评论(2) 编辑收藏举报

刷新页面返回顶部

genshy

线段树合并 从入门到入土

大体的实现思路：

1.合并区间最大值

2.合并区间和

P3605 [USACO17JAN]Promotion Counting P

P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并

P3224 [HNOI2012]永无乡

P4197 Peaks

公告

线段树合并从入门到入土