P3469 BLO-Blockade

又可以水紫题了，好开心

题意描述：

给定一张无向图，求每个点被封锁之后有多少个有序点对 \((x,y)(x!=y,1<=x,y<=n)\) 满足 \(x\) 无法到达 \(y\)

数据范围： \(n\leq 10^5\)

solution

前置芝士: 无向图割点，然后脑子。。。

首先，对于这道题，我们要求的是，割去每个点及他所连的边后，无向图中，有多少有序点对（\(x\),\(y\)）满足 \(x\),\(y\) 互不连通

我们思考一下，这道题既然跟点有关，那么我们可以想到，在无向图中，我们可以把所有的点分为两种，割点和非割点。

我们大力讨论一下。。。。

1.对于非割点

把他去掉之后，就会发生这样的事情，

样例原始图是这样

5不是割点，去掉她以及他连的边后

就会成这样

他就会与剩下\(n-1\)个点，不相连，那么他的\(ans\)就是\(2\times (n-1)\)

2.对于割点

其实不难，请同学自证

假如 \(j\) 是割点把 \(j\) 割掉后，图就会分成好几个联通快。那么求出每个连通块的大小，再分别乘起来就行。

我们把它放到搜索树上考虑，这几种连通块就会有以下几种情况

1. 割点 \(j\) 单独成一个块。
2. \(j\) 的每个子树都是一个连通块
3. 除了 \(j\) 和他子树中的点，其他点构成一个连通块

就像这样

原图

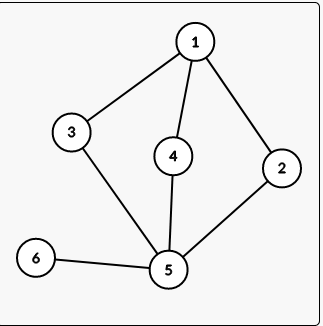
5是割点

割去5后，变成这样

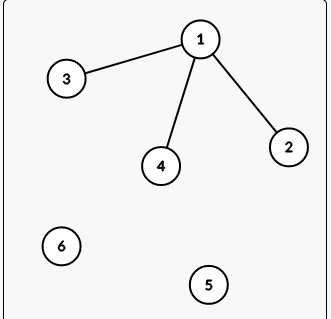
他的搜索树长这样

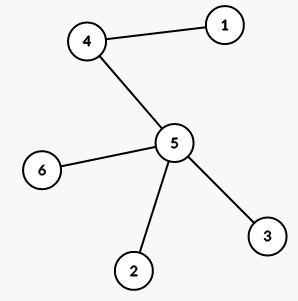
他的子树 6 ，2 ， 3 各成一个联通快

它上面的 1 4 节点成一个连通块

他自己又成一个联通块

因此割点的答案就是

\(\displaystyle\sum_{k = 1}^{k}size_i\times (n-size_i)\) + (\(n\)-\(sum + 1\)) * (\(sum + 1\)) + (\(n-1\));

\(sum\) 是他子树的大小，\(n-sum+1\) 为剩下的大联通块的大小，\(sum+1\)就是他自己和他子树的大小

code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int n,m,x,y,tot,num,root;
int head[N],dfn[N],low[N],size[N];
long long ans[N];
bool cut[N];
struct node{int to ,net;} e[500100*2]; 
inline int read()
{
	int s = 0 , w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s =s * 10+ch - '0'; ch = getchar();}
	return s * w;
}
void add(int x,int y)
{
	e[++tot].to = y;
	e[tot].net = head[x];
	head[x] = tot;
}
void tarjain(int x)
{
	dfn[x] = low[x] = ++num; size[x] = 1;
	int flag = 0,sum = 0;//sum是子树和
	for(int i = head[x]; i; i = e[i].net)
	{
		int to = e[i].to;
		if(!dfn[to])
		{
			tarjain(to);
			size[x] += size[to];//统计一下他的size
			low[x] = min(low[x],low[to]);
			if(low[to] >= dfn[x])
			{
				flag++;
				ans[x] += (long long) size[to] * (n - size[to]);//统计一下他子树的贡献
				sum += size[to];
				if(x != root || flag > 1) cut[x] = true;
			}
		}
		else low[x] = min(low[x] , dfn[to]);
	}
	if(cut[x] = true) ans[x] += (long long) (n - sum - 1) * (sum + 1) + (n-1);//最后加上他的贡献和其他点的贡献
	else ans[x] = 2 * (n-1);//非割点的情况
}
int main()
{
	n = read(); m = read();
	for(int i = 1; i <= m; i++)
	{
		x = read(); y = read();
		add(x,y); add(y,x);
	}
	root = 1; tarjain(1);
	for(int i = 1; i <= n; i++) printf("%lld\n" , ans[i]);
	return 0;
}