倍增
倍增
倍增法,字面上看起来是翻倍。这种方法在很多算法中都有应用。比较常见的就是RMQ问题,
以及倍增求LCA
例题 给出一个长度为n的环,每次从第i个点跳到(i+k) mod n+1 个点,总共跳了m次。每个点
都有一个权值,记为a[i], 求m次起跳起点的权值之和对1e9+7取模的结果。
数据范围: 1 ≤ n ≤ 10^6, 1 ≤ m ≤ 10^18, 1 ≤ k ≤ n, 0 ≤ a[i] ≤ 10^9.
显然我们不可能暴力模拟跳m次,因为m最大可以达到10^18,这样会炸时间。所以,我们需要考虑进行一些预处理,提前整合出一些信息,以便查询。
那怎么预处理呢??? 再看一道题
如何用尽可能的砝码称量出[0,31]所有的重量。
答案是使用1 2 4 8 16 这五个砝码,同理,如果要称[0,127]之间的重量,可以使用1 2 4 8 16 32 64这七个砝码。 每次我们都选2的整次幂最为砝码重量,
就可以使用极少的砝码个数,称出任意我们需要的数量。
为什么是极少呢? 因为如果我们目标重量翻倍,那么砝码个数只需要增加1.这种增长速度还是比价可观的。
那么对于第一道例题,我们可以预处理从每个点开始跳1,2,4,8等2^j步的结果。 然后举个例子,当跳13步时,我们只需要跳1+4+8 步就好了,也就是从
起始点跳1步,然后在从跳了之后的终点跳4步
再接着跳8步。同时统计一下预选处理好的点权和,就可以知道跳13步的点权和了。
对于每个点 记录一个 go[i][j] 表示从第i个点,跳2^j 步的终点, sum[i][j] 表示从第x个点跳2^j能获得
的点权和。预处理时,开两重循环,我们可以看做先跳了2^(j-1) ,在跳了2^(j-1) 步,因为 2 * 2^(j-1)= 2 ^j .
所以递推式就是
1 sum[i][j] = sum[i][j-1] + sum [go[i][j-1]] [j-1]; 2 go[i][j] = go[go[i][j-1]] [j-1]
一些小细节就是,为了保证不重复计算,我们一般处理处左闭右开的点权和。即对于每跳一次,我们只记录起点和中间点的点权和
,相当于不将重点计入sum,这样就会保证不重复计算
1 #include<iostream> 2 #include<algorithm> 3 #include <cstdio> 4 using namespace std; 5 6 const int mod = 1000000007; 7 8 int vi[1000005]; 9 10 int go[75][1000005]; // 将数组稍微开大以避免越界,小的一维尽量定义在前面 11 int sum[75][1000005]; 12 13 int main() { 14 int n, k; 15 scanf("%d%d", &n, &k); 16 for (int i = 1; i <= n; ++i) { 17 scanf("%d", vi + i); 18 } 19 20 for (int i = 1; i <= n; ++i) { 21 go[i][0] = (i + k) % n + 1; 22 sum[i][0] = vi[i]; 23 } 24 25 int logn = log(n); // 一个快捷的取对数的方法 26 for (int i = 1; i <= logn; ++i) { 27 for (int j = 1; j <= n; ++j) { 28 go[i][j] = go[go[i][j-1]][j-1]; 29 sum[i][j] = sum[i][j-1] + sum[go[i][j-1]] [j-1] % mod; 30 } 31 } 32 33 long long m; 34 scanf("%lld", &m); 35 36 int ans = 0; 37 int curx = 1; 38 for (int i = 0; m; ++i) { 39 if (m & (1 << i)) { //意为 m 的第 i 位是否为 1 40 ans = (ans+ sum[curx][i])) % mod; 41 curx = go[curx][i]; 42 m ^= 1ll << i; // 将第 i 位置零 43 } 44 } 45 46 printf("%d\n", ans); 47 }
这种做法的时间复杂度是 预处理O(nlogm) 查询复杂度为 每次O(logm);
RMQ问题
RMQ 问题就是区间最大值(最小值)问题
用倍增解决RMQ问题,其实就是ST表
ST表可以做到 O(nlogn)预处理 O(1) 的回答
f[i][j] 表示 区间 [j,i+2^j-1] 的最大值
初值 f[i][0] = a[i];
转移方程式 就是
1 f[i][j] = max(f[i][j-1],f[i+(1<<(j-1)] [j-1]
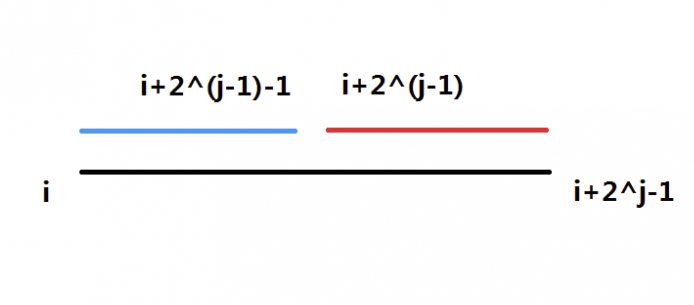
对于每个询问,我们可以把它分成两部分 f[L][s] 与 f[ R-(1<<s)+1][s]
其中 s = log(r-l+1)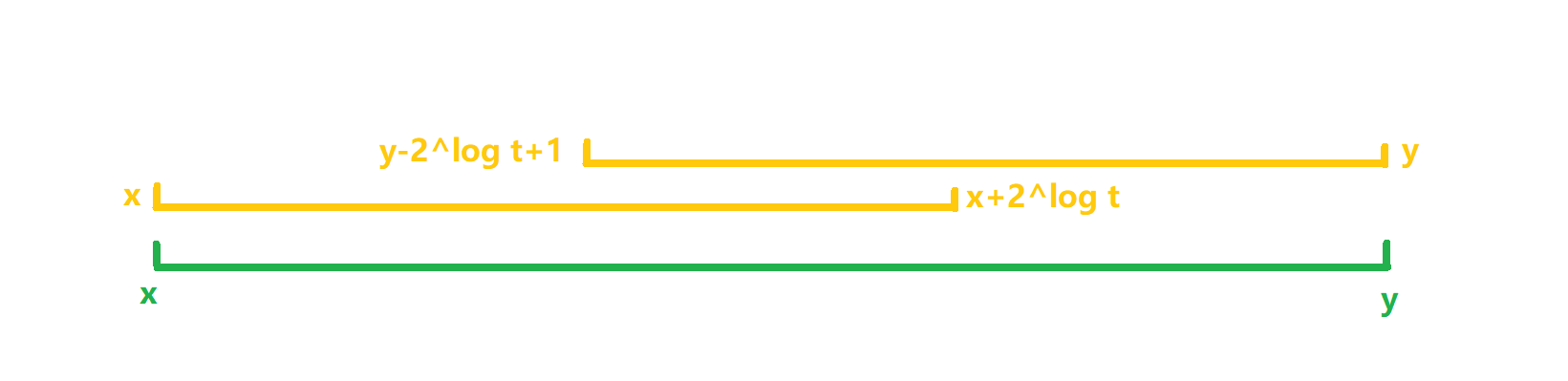
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int N = 1e5+10; 6 int n,m,ans,x,l,r,tmp; 7 int f[N][21],lg[N]; 8 inline int read() 9 { 10 int x=0,f=1;char ch=getchar(); 11 while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();} 12 while (isdigit(ch)){x=x*10+ch-48;ch=getchar();} 13 return x*f; 14 } 15 int main(){ 16 n = read(), m = read(); 17 lg[0] = -1; 18 for(int i = 1; i <= n; i++){ 19 f[i][0] = read(); 20 lg[i] = lg[i>>1] +1;//预处理每个数的log() 21 } 22 for(int j = 1; j <= 20; j++){ 23 for(int i = 1; i + (1<<j)-1 <= n; i++){ 24 f[i][j] = max(f[i][j-1],f[i+(1<<(j-1))][j-1]);//预处理f数组 25 } 26 } 27 for(int i = 1; i <= m; i++){ 28 l = read(), r = read(); 29 tmp = lg[r-l+1]; 30 ans = max(f[l][tmp],f[r-(1<<tmp)+1][tmp]);//O(1)查询 31 printf("%d\n",max(f[l][tmp],f[r-(1<<tmp)+1][tmp])); 32 } 33 return 0; 34 }
RMQ问题还可以用线段树来写,时间也比倍增要快很多,倍增维护RMQ一般没人用
例题——>降雨量(这道题区间有序的,直接用lower_bound就行了,没必要用倍增)
习题: 平衡的阵容
倍增求LCA
也没有什么可以讲的,我主要用树剖求LCA,不但快还不容易被卡QAQ。
象征性放个代码

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<queue> 6 using namespace std; 7 8 const int N = 5e5+100; 9 int n,m,x,y,tot,s; 10 int d[N],p[N][23],head[N]; 11 12 struct tree{ 13 int to; 14 int net; 15 }e[N<<1]; 16 void add(int x,int y){ 17 tot++; 18 e[tot].to = y; 19 e[tot].net = head[x]; 20 head[x] = tot; 21 } 22 void dfs1(int x,int fa){ 23 d[x] = d[fa] +1; 24 // deep[x] = d[x]; 25 // manx = max(manx,d[x]); 26 p[x][0] = fa; 27 for(int i = 1; i<= 20; i++){ 28 p[x][i] = p[p[x][i-1]][i-1]; 29 } 30 for(int i = head[x]; i; i =e[i].net){ 31 int to = e[i].to; 32 if(to != fa) dfs1(to,x); 33 } 34 } 35 36 int lca(int a,int lp) 37 { 38 if(d[a]>d[lp]) swap(a,lp); 39 for(int i=20;i>=0;i--) 40 { 41 if(d[a]<=d[lp]-(1<<i)) 42 { 43 lp=p[lp][i]; 44 } 45 } 46 if(a==lp) return a; 47 for(int i=20;i>=0;i--) 48 { 49 if(p[a][i]!=p[lp][i]) 50 a=p[a][i],lp=p[lp][i]; 51 } 52 return p[a][0]; 53 } 54 int main(){ 55 scanf("%d%d%d",&n,&m,&s); 56 for(int i = 1; i <= n-1; i++){ 57 scanf("%d%d",&x,&y); 58 add(x,y); 59 add(y,x); 60 } 61 dfs1(s,0); 62 for(int i = 1; i <= m; i++){ 63 scanf("%d%d",&x,&y); 64 cout<<lca(x,y)<<endl; 65 } 66 return 0; 67 }





