莫比乌斯反演
莫比乌斯反演相关
莫比乌斯函数

狄利克雷卷积
设f(n)、g(n)是两个数论函数,它们的狄利克雷乘积也是一个数论函数,其定义为:
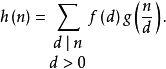
简记为h(n)=f(n)*g(n)。
函数f(n)与g(n)的狄利克雷乘积也可以表示为

常用狄利克雷卷积
1.
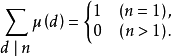
3.
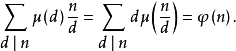
4.
5.
莫比乌斯反演
设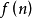 和
和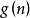 是定义在正整数集合上的两个函数,定义如下。
是定义在正整数集合上的两个函数,定义如下。
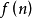 和
和
若函数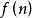 满足:
满足:

则有
例题
求1<=i<=n,1<=j<=m,gcd(i,j)==d的对数。
先让n/=d,m/=d,变成求gcd(i,j)==1的对数。
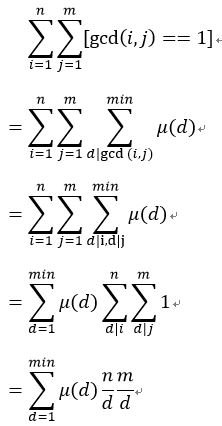
然后预处理出μ(d)的前缀和,O(sqrt(n))枚举d即可。
代码
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define lli long long int using namespace std; const int maxn=5e4+1e2; int mu[maxn]; lli sum[maxn]; inline void gen() { static int prime[maxn],cnt; static unsigned char vis[maxn]; sum[1] = mu[1] = 1; for(int i=2;i<maxn;i++) { if( !vis[i] ) { prime[++cnt] = i, mu[i] = -1; } for(int j=1;j<=cnt&&i*prime[j]<maxn;j++) { vis[i*prime[j]] = 1; mu[i*prime[j]] = -mu[i]; if( ! ( i % prime[j]) ) { mu[i*prime[j]] = 0; break; } } sum[i] = sum[i-1] + mu[i]; } } inline lli calc(int n,int m) { lli ret = 0; if( n > m ) swap(n,m); int pos = 0; for(int i=1;i<=n;i=pos+1) { pos = min( n / ( n / i ) , m / ( m / i ) ); ret += ( sum[pos] - sum[i-1] ) * ( n / i ) * ( m / i ); } return ret; } int main() { static int T; int a,b,d; gen(); scanf("%d",&T); while( T-- ) { scanf("%d%d%d",&a,&b,&d); a /= d , b /= d; printf("%lld\n",calc(a,b)); } return 0; }


