题解报告——扇形面积并
题目描述
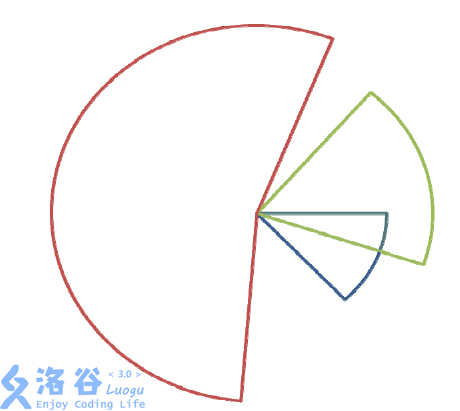
给定 n 个同心的扇形,求有多少面积,被至少k 个扇形所覆盖。
输入输出格式
输入格式:
第一行是三个整数 n,m,k。n 代表同心扇形个数,m代表将(−π ,π ]的角度
区间平均分成2m 份。
从第二行开始的 n 行,每行三个整数r,a1,a2。描述了一个圆心在原点的
扇形,半径为r,圆心角是从弧度
π∗a1/mπ*a1/mπ∗a1/m到π∗a2/mπ*a2/mπ∗a2/m(a1 不一定小于 a2)。
输出格式:
输出一个整数 ans ,π/2m∗ansπ/2m*ansπ/2m∗ans等于至少k 个扇形所覆盖的总面积。
数据保证答案在263−12^{63} - 1263−1范围内。
输入输出样例
说明
1≤n≤10^5, 1≤m≤10^6,1≤k≤5000,1≤ri≤10^5,-m≤a1,a2≤m
【思路分析】
第一眼看到这个题以为是计算几何,一看通过数也不多,又是一道算几毒瘤题。。。但是我们仔细看看,发现数据都是整数,并且良心出题人将输出数据都为你做成了整数,感觉似乎就不像毒瘤算几了??!!再观察发现将圆划分成了相等的几块小区间,顿时感觉这道题变更成了区间问题了,我们尝试用线段树搞一搞??!!
对于查询被至少k个扇形覆盖的区间,等同于查询当前区间覆盖了扇形的第k大半径,既然有k的存在,那么数据结构无非就是平衡树和权值线段树,发现区间很多,平衡树不方便维护区间与区间之间的关系,那么我们考虑用权值线段树,区间k大问题??主席树板题??!!,其实不然,我们并不需要用主席树,只用开一棵权值线段树即可。
我们将扇形按起点排序,发现这就有点类似于扫描线,有下边界,有上边界,差分维护扇形起点终点即可。
然而我们发现这道题是有环的,即一个扇形的可能跨过我们的起点(而矩形面积并则不会),我们只需要将这样的扇形拆分成两块维护即可。。。AC了??!!
这次就真的应该可以A了!!!
【代码实现】
1 #include<cstdio> 2 #include<cctype> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 typedef long long ll; 8 void read(int &x) 9 { 10 int f;char ch; 11 while(!isdigit(ch=getchar())&&ch!='-'); ch=='-'?(f=-1,x=0):(f=1,x=ch-'0'); 12 while(isdigit(ch=getchar())) x=x*10+ch-'0';x=x*f; 13 } 14 const int N=1e5+5,M=1e6+5; 15 struct sd{ 16 int son[2],num; 17 }t[N<<1]; 18 int n,m,k,cnt,root,mx; 19 vector<int> cf[M<<1]; 20 void insert(int &v,int l,int r,int pos,int add) 21 { 22 if(!v) v=++cnt;t[v].num+=add; 23 if(l==r) return; 24 int mid=l+r>>1; 25 if(pos<=mid) insert(t[v].son[0],l,mid,pos,add); 26 else insert(t[v].son[1],mid+1,r,pos,add); 27 } 28 int ask(int v,int l,int r,int k) 29 { 30 if(l==r) return l; 31 int mid=l+r>>1,ls=t[v].son[0],rs=t[v].son[1]; 32 if(t[ls].num>=k) return ask(ls,l,mid,k); 33 else return ask(rs,mid+1,r,k-t[ls].num); 34 } 35 ll mul(ll a){return a*a;} 36 int main() 37 { 38 int l,r,ri; 39 read(n),read(m),read(k); 40 for(int i=1;i<=n;i++){ 41 read(ri),read(l),read(r); 42 l+=m+1,r+=m; 43 if(l==2*m+1) l=1;if(r==2*m) r=-1; 44 if(r==-1) cf[l].push_back(ri); 45 else if(l>r) cf[l].push_back(ri),cf[1].push_back(ri),cf[r+1].push_back(-ri); 46 else cf[l].push_back(ri),cf[r+1].push_back(-ri); 47 mx=max(ri,mx); 48 } 49 ll ans=0; 50 for(int i=1;i<=2*m;i++) 51 { 52 int ss=cf[i].size(); 53 for(int j=0;j<ss;j++) 54 if(cf[i][j]>0){ 55 int gg=cf[i][j]; 56 insert(root,1,mx,cf[i][j],1); 57 } 58 else insert(root,1,mx,-cf[i][j],-1); 59 if(t[root].num>=k) ans=ans+mul(1ll*ask(root,1,mx,t[root].num-k+1)); 60 } 61 printf("%lld",ans); 62 return 0; 63 }

