题解报告——寿司晚宴
题目描述
为了庆祝NOI的成功开幕,主办方为大家准备了一场寿司晚宴。小G和小W作为参加NOI的选手,也被邀请参加了寿司晚宴。
在晚宴上,主办方为大家提供了n−1种不同的寿司,编号1,2,3,⋯,n-1,其中第种寿司的美味度为i+1(即寿司的美味度为从2到n)。
现在小G和小W希望每人选一些寿司种类来品尝,他们规定一种品尝方案为不和谐的当且仅当:小G品尝的寿司种类中存在一种美味度为x的寿司,小W品尝的寿司中存在一种美味度为y的寿司,而x与y不互质。
现在小G和小W希望统计一共有多少种和谐的品尝寿司的方案(对给定的正整数p取模)。注意一个人可以不吃任何寿司。
输入输出格式
输入格式:
从文件dinner.in中读入数据。
输入文件的第1行包含2个正整数n,p中间用单个空格隔开,表示共有n种寿司,最终和谐的方案数要对p取模。
输出格式:
输出到文件dinner.out中。
输出一行包含1个整数,表示所求的方案模p的结果。
输入输出样例
说明
【数据范围】
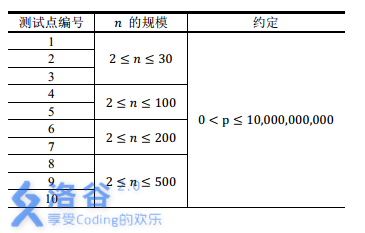
【时限1s,内存512M】
【思路分析】
首先看到这道题时,我第一个想法是容斥,我们只需要求出不和谐的方案数即可,然而我们可以n^2预处理出不和谐的数字对数,然后我们枚举1对,2对,3对……然后容斥一下,隔项添一个负号,结果发现GG,因为比如2 3 4,我们发现我们在3对时枚举到这种情况,然而实际上有4对。所以就只有放弃容斥的想法了。
再看数据范围,我们考虑一下是不是可以DP之类的,我们设dp[i][j][k]表示选到第i个数,第一个人所拥有的质因数的二进制表示为j,第二个人所拥有的质因数的二进制表示为k,然后就可以进行转移,然而发现500以内的质因数个数并不少,这个方法只能让我们拿到30分。这是应该出现的惯性思维便是,我们只存储√n的质因数,也就是最大到19,发现这样只有8个需要状压一下。
这里发现dp[i]只与dp[i-1]有关,所以我们可以滚动掉第一维。
我们用f1[i][j],f2[i][j]分别表示当前的第一个人选这个数,或第二个人选这个数的状态。
得到转移方程 :
f1[i|k][j]+=f1[i][j] (j&k==0)
f2[i][j|k]+=f2[i][j] (i&k==0)
dp[i][j]=f1[i][j]+f2[i][j]-dp[i][j]
这里的dp[i][j]为上一次转移后的dp[i][j],因为要排除掉什么质因数也没增加的情况
最后答案就是所有的dp[i][j]之和。
这里还有遗漏的一点就是我们还没考虑超过√n的质因数,我们只需要将这些数按最大质因数大小排个序,拥有大于√n的质因数的数选一个就好,然后取最大值即可,具体看代码实现。
【代码实现】
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<cctype> 5 using namespace std; 6 typedef long long ll; 7 void read(ll &x) 8 { 9 char ch;ll f; 10 while(!isdigit(ch=getchar())&&ch!='-'); ch=='-'?(x=0,f=-1):(x=ch-'0',f=1); 11 while(isdigit(ch=getchar())) x=x*10+ch-'0'; 12 } 13 const int N=505,M=260; 14 int pp[9]={0,2,3,5,7,11,13,17,19}; 15 struct sd{ 16 int val,p,big; 17 void divide(){ 18 for(int i=1;i<=8;i++) 19 while((val%pp[i])==0) 20 val=val/pp[i],p=p|(1<<(i-1)); 21 big=val; 22 } 23 }st[N]; 24 int n; 25 ll mod,dp[M][M],f1[M][M],f2[M][M],ans; 26 bool cmp(sd a,sd b){return a.big<b.big;} 27 int main() 28 { 29 scanf("%d%lld",&n,&mod); 30 for(int i=2;i<=n;i++) st[i].val=i,st[i].divide(); 31 sort(st+2,st+1+n,cmp); 32 dp[0][0]=1; 33 for(int now=2;now<=n;now++) 34 { 35 if(now==2||st[now].big==1||st[now].big!=st[now-1].big) 36 memcpy(f1,dp,sizeof(f1)),memcpy(f2,dp,sizeof(f2)); 37 for(int i=255;i>=0;i--) 38 for(int j=255;j>=0;j--) 39 { 40 if(i&j) continue; 41 if(!(i&st[now].p)) f2[i][j|st[now].p]=(f2[i][j|st[now].p]+f2[i][j])%mod; 42 if(!(j&st[now].p)) f1[i|st[now].p][j]=(f1[i|st[now].p][j]+f1[i][j])%mod; 43 } 44 if(now==n||st[now].big==1||st[now].big!=st[now+1].big) 45 for(int i=255;i>=0;i--) 46 for(int j=255;j>=0;j--) 47 if(!(i&j))dp[i][j]=(f1[i][j]+f2[i][j]-dp[i][j])%mod; 48 } 49 for(int i=255;i>=0;i--) 50 for(int j=255;j>=0;j--) 51 if(!(i&j)&&dp[i][j]) ans=(ans+dp[i][j])%mod; 52 printf("%lld",(ans%mod+mod)%mod); 53 return 0; 54 }


