题解报告——水平可见直线

传送门

在xoy直角坐标平面上有n 条直线L1,L2,...Ln ,若在y 值为正无穷大处往下看,能见到Li 的某个子线段,则称Li 为可见的,否则Li 为被覆盖的。

例如,对于直线:

L1:y=x

L2:y=−x

L3:y=0

则L1 和L2 是可见的,L3 是被覆盖的.

给出n 条直线,表示成y=Ax+B 的形式(|A|,|B|≤500000 ),且n 条直线两两不重合.求出所有可见的直线.

【输入】

第一行为N(0<N<50000) ,接下来的NN 行输入Ai,Bi

【输出】

从小到大输出可见直线的编号，两两中间用空格隔开,最后一个数字后面也必须有个空格

【输入样例】

3
-1 0
1 0
0 0

【输出样例】

1 2

---

 【思路分析】

首先我们可以得出，我们最后从上方看到的直线排布，一定是一个类似于下凸包的形状，将这些直线按其k值从小到大排一下序，如果k相同则按b从小到大排序，依次加到栈中，我们判断一下交点的位置关系，如下图：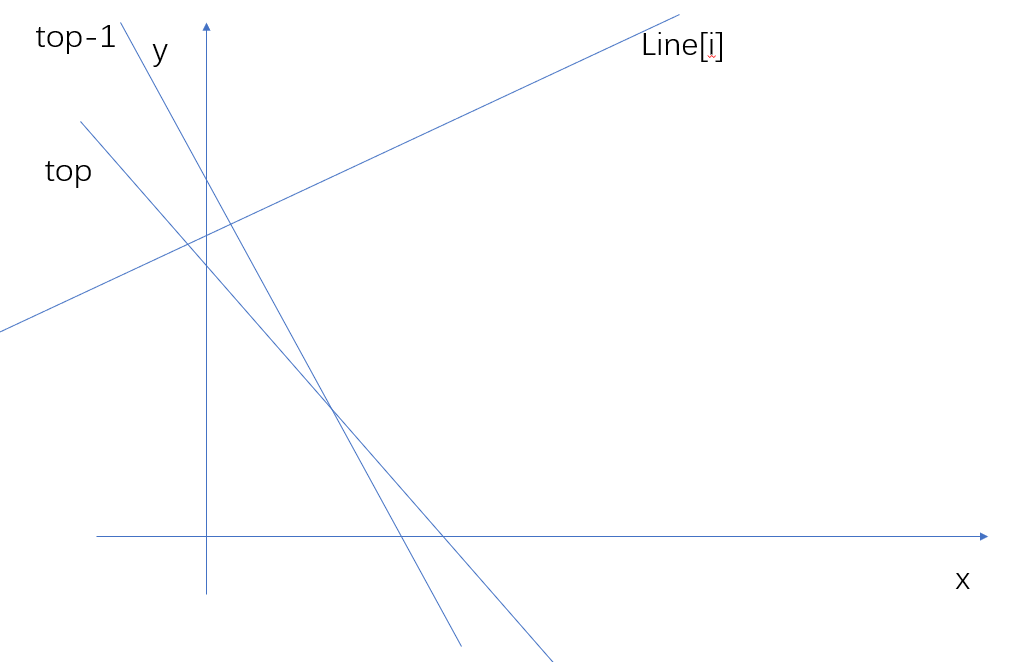

我们发现如果line[i]与top的交点的x小于line[i]与top-1的交点的x，那么top这条直线就被完全覆盖了，就要将其弹出。

最后我们就统计一下留在栈中的直线即可

---

 

【代码实现】

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=5e4+5;
struct sd{
    double k,b;int id;
}line[N],stk[N];
int n,top;
bool cmp(sd a,sd b)
{
    if(a.k==b.k) return a.b<b.b;
    return a.k<b.k;
}
bool CMP(sd a,sd b){return a.id<b.id;}
double mix(sd x,sd y){return (y.b-x.b)/(x.k-y.k);}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    scanf("%lf %lf",&line[i].k,&line[i].b),line[i].id=i;
    sort(line+1,line+1+n,cmp);
    for(int i=1;i<=n;i++)
    {
        while(top>0&&line[i].k==stk[top].k) top--;
        while(top>1&&mix(line[i],stk[top])<=mix(line[i],stk[top-1])) 
        top--;
        stk[++top]=line[i];
    }
    sort(stk+1,stk+1+top,CMP);
    for(int i=1;i<=top;i++) printf("%d ",stk[i].id);
    return 0;
}