线段树扫描线
火星探险(mars)
时间限制: 1000 ms 内存限制: 131072 KB【题目描述】
在2051年,若干火星探险队探索了这颗红色行星的不同区域并且制作了这些区域的地图。现在,Baltic空间机构有一个雄心勃勃的计划,他们想制作一张整个行星的地图。为了考虑必要的工作,他们需要知道地图上已经存在的全部区域的大小。你的任务是写一个计算这个区域大小的程序。
具体任务要求为:
(1)从输入中读取地图形状的描述;
(2)计算地图覆盖的全部的区域;
(3)输出探索区域的总面积(即所有矩形的公共面积)。
【输入】
输入的第一行包含一个整数n(1≤n≤10000),表示可得到的地图数目。
以下n行,每行描述一张地图。每行包含4个整数x1,y1,x2和y2(0≤x1<x2≤30000,0≤y1<y2≤30000)。数值(x1,y1)和(x2,y2)是坐标,分别表示绘制区域的左下角和右上角坐标。每张地图是矩形的,并且它的边是平行于x坐标轴或y坐标轴的。
【输出】
输出文件包含一个整数,表示探索区域的总面积(即所有矩形的公共面积)。
【输入样例】
2 10 10 20 20 15 15 25 30
【输出样例】
225
对于这种题我们的正解就是线段树套扫描线,听起来是不是逼格很高。
一、什么是扫描线
什么是扫描法?有什么用?怎么用?
可以想象成一根假想的线,将图从左往右或从右往左或自下而上或自上而下“扫描”一遍,至于扫描的是什么则根据具体应用选择。
扫描线可以计算矩形面积、周长,可以计算线段交点,可以实现多边形扫描转换,在图的处理方面经常用到。
这里总结一下扫描线计算矩形面积的算法。
怎么用?首先,对于之前的图,除了用总面积减去重合面积,还可以换一种计算方法,如图:
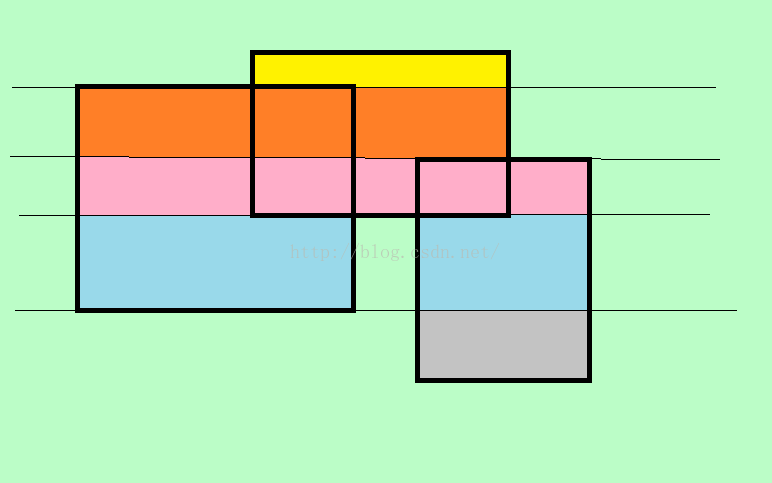
此图用4条横线将整个图划分成了5个部分,显然此时再算面积就可以用各个颜色的部分求和。
想想,这样计算的整个慢过程:
假设我们的视线自下而上,首先,我们看到了最下面灰色矩形的下边,
用这个下边的长度乘以这条边和上一条边的高度差即得到灰色矩形面积,
继续看到蓝色的矩形的下边,虽然蓝色矩形有两个,但我们计算时自然会用结合律将两个矩形的下边加起来再去乘以同样的高,
然后重复这样的操作,我们最终可以求得整个图形的面积。
二、计算机实现
但是,这依旧是人做的,计算机要怎么实现呢?
首先的问题是,计算机要怎么保存这张图这些矩形?
从刚才的过程,我们不难发现,我们只需要保存这张图里面的所有水平的边即可。
对于每条边,它所拥有的属性是:这条边的左右端点(的横坐标),这条边的高度(纵坐标),这条边属于矩形的上边还是下边(想想为什么保存这个属性)
刚刚计算中我们遇到两个蓝色矩形的一部分一眼就能看出这两个蓝色矩形的‘宽’是多少,用计算机怎么做到?
线段树华丽登场!
我们以整个图最左边的竖线作为区间左端点,最右边的竖线作为区间右端点,去维护这个区间的有效长度(即被覆盖的长度)
比如扫到第2条边的时候,有效长度就是两个蓝色矩形的宽之和。
这样,我们用扫描线去扫描每一条边的时候,都需要更新线段树的有效长度
是如何更新的呢?
如果扫到的这条边是某矩形的下边,则往区间插入这条线段
如果扫到的这条边是某矩形的上边,则往区间删除这条线段
为什么?自己试着模拟一下就不难发现:
因为我们是自下而上的扫这个图,扫到下边相当于刚刚进入一个矩形,扫到上边则是要离开一个矩形
利用线段树把每条边的有效长度找到了,也就是找到了每部分的所有矩形的总宽,那么高呢?
高就简单多了,对于所有的边,按照高度从小到大排列,那么矩形高就是每相邻边之间的高度差
三、手推一波
-
扫描线扫描的过程(建议配合代码模拟)
初始状态
扫到最下边的线, 点1→31→3更新为11
扫到第二根线, 此时S=lcnt!=0∗h两根线之间S=lcnt!=0∗h两根线之间, 得到绿色的面积, 加到答案中去, 随后更新计数
同上, 将黄色的面积加到答案中去
同上, 将灰色的面积加到答案中去
同上, 将紫色的面积加到答案中去
同上, 将蓝色的面积加到答案中去
四、代码实现
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 struct edge{ 5 int h,lx,rx,s; 6 bool operator < (const edge &b) const 7 { 8 return h<b.h; 9 } 10 }line[20005]; 11 struct sd{ 12 int son[2],l,r,len,s;//线段树左右儿子,区间范围,覆盖线段层数 13 }t[200005];//ps.线段树区间记录的是竖线的编号 14 int X[20005];//记录竖着的边的x值 15 int cnt; 16 void build(int &v,int l1,int r1)//线段树建树 17 { 18 cnt++;v=cnt; 19 t[v].l=l1,t[v].r=r1; 20 if(l1==r1) return; 21 int mid=(l1+r1)>>1; 22 build(t[v].son[0],l1,mid); 23 build(t[v].son[1],mid+1,r1); 24 } 25 int find(int l1,int r1,int key)//二分查询当前位置所属线段编号,便于在线段树中查询 26 { 27 while(l1<=r1) 28 { 29 int mid=(l1+r1)/2; 30 if(X[mid]==key) return mid; 31 else 32 if(X[mid]<key) l1=mid+1; 33 else r1=mid-1; 34 } 35 } 36 void pushup(int v)//更新 37 { 38 if(t[v].s) 39 t[v].len=X[t[v].r+1]-X[t[v].l];//如果有线段覆盖标记那就直接将标记赋值,不用下传标记,因为每次查询整个区间 40 else 41 if(t[v].l==t[v].r) 42 t[v].len=0; 43 else 44 t[v].len=t[t[v].son[0]].len+t[t[v].son[1]].len;//更新线段覆盖长度 45 } 46 void update(int v,int l1,int r1,int c)//修改操作 47 { 48 if(t[v].l==l1&&t[v].r==r1) 49 { 50 t[v].s+=c;//区间覆盖标记 51 pushup(v); 52 return; 53 } 54 int mid=(t[v].l+t[v].r)>>1; 55 if(l1>mid) update(t[v].son[1],l1,r1,c); 56 else 57 if(r1<=mid) update(t[v].son[0],l1,r1,c); 58 else 59 { 60 update(t[v].son[0],l1,mid,c); 61 update(t[v].son[1],mid+1,r1,c); 62 } 63 pushup(v); 64 } 65 int main() 66 { 67 int n; 68 scanf("%d",&n); 69 int tot=0; 70 for(int i=1;i<=n;i++) 71 { 72 int x1,x2,y1,y2; 73 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 74 tot++; 75 line[tot].lx=x1,line[tot].rx=x2,line[tot].h=y1,line[tot].s=1; 76 X[tot]=x1; 77 tot++; 78 line[tot].lx=x1,line[tot].rx=x2,line[tot].h=y2,line[tot].s=-1; 79 X[tot]=x2; 80 } 81 sort(X+1,X+1+tot); 82 sort(line+1,line+1+tot); 83 int root; 84 build(root,1,tot); 85 int k=0; 86 for(int i=1;i<=tot;i++)//离散化 87 { 88 if(X[i]!=X[i+1]) 89 { 90 k++,X[k]=X[i]; 91 } 92 } 93 long long res=0; 94 for(int i=1;i<=tot;i++) 95 { 96 int ll=find(1,k,line[i].lx);//找到当前区间左端点竖线编号 97 int rr=find(1,k,line[i].rx)-1;//当前区间右端点的竖线编号 98 update(1,ll,rr,line[i].s); 99 res+=(line[i+1].h-line[i].h)*t[1].len;//统计面积 100 } 101 printf("%lld",res); 102 return 0; 103 }

