多粒度粗糙集理论及其相关约简
引言：K=<U,R>为一个知识基，根据不同知识的划分p1,p2，...，pn得到了一个多粒度空间，记为MK（U）={U/IND（p1），U/IND（p2），...U/IND（pn）}
我们在这个多粒度空间的基础上再来讨论多粒度粗糙集，其中多粒度粗糙集研究模型有两大类：乐观多粒度粗糙集和悲观多粒度粗糙集，两者对于粗糙集的上下近似定义有所区分：
1.乐观多粒度粗糙集上下近似：
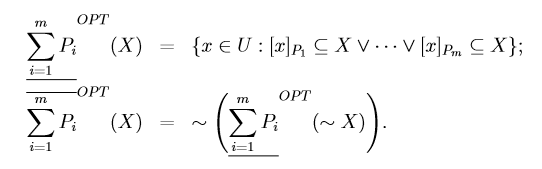
其中乐观多粒度粗糙集的下近似是：对象X对一个或者多个等价类是否包含于目标集和，若加上精度B（[0.5,1]）判别包含关于是否大于B，则可引申为变精度多粒度粗糙集。
乐观多粒度粗糙集的上近似是：对乐观多粒度下近似的补集加以定义。
2.悲观多粒度粗糙集上下近似：
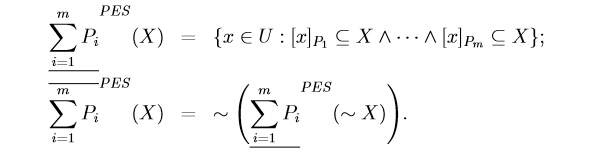
其中悲观多粒度粗糙集的下近似是：对象X多个等价类都包含于目标集和，若加上精度B（[0.5,1]）判别包含关于是否大于B，则可引申为变精度多粒度粗糙集。
悲观多粒度粗糙集的上近似是：对悲观多粒度下近似的补集加以定义。
本文将以乐观多粒度粗糙集作为研究对象，对于悲观多粒度粗糙集改变相关算法即可不再赘述。
3.求解上下近似。
3.1先利用上段中乐观多粒度粗糙集上下近似求解方法求解：
例：U={e1，e2，....，e8}表示有8个人，条件属性m={身高，体重，学历}，决策属性为D={是否有女朋友}，得到下列决策表（纯属虚构用于理解）。
| 论域U | 身高L | 体重I | 学历P | 是否有女友D |
| e1 | 中等 | 胖 | 研究生 | 有 |
| e2 | 矮子 | 胖 | 研究生 | 有 |
| e3 | 矮子 | 瘦 | 高中生 | 无 |
| e4 | 矮子 | 瘦 | 高中生 | 无 |
| e5 | 矮子 | 瘦 | 高中生 | 无 |
| e6 | 矮子 | 胖 | 大学生 | 有 |
| e7 | 中等 | 胖 | 大学生 | 无 |
| e8 | 很高 | 胖 | 大学生 | 有 |
D={X1，X2}，其中X1表示有，X2表示无。
X1={e1,e2,e6,e8}, X2={e3,e4,e5,e7}
L={{e1,e7},{e2,e3,e4,e5,e6},{e8}}
I={{e1,e2,e6,e7,e8},{e3,e4,e5}}
p={{e1,e2},{e3,e4,e5},{e6,e7,e8}}
所以对于X1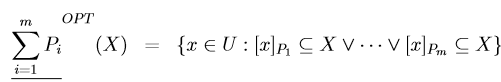
求得={e1,e2,e8}
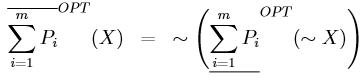=U
同理求得X2下近似为{e3,e4,e5}
X2的上近似为U
4.求解多粒度粗糙集正域及其约简
4.1多粒度粗糙集正域：
与普通粗糙集不同，多粒度粗糙集的正域是所有不同决策属性下近似的交集：
如上例子中，正域为X1下近似 U X2下近似={e1,e2,e3,e4,e5,e8}.
4.2多粒度粗糙集正域的约简：
在属性集中若B属于A，且B的正域与A的正域等价，同时满足C属于B，且C的正域与A的正域不等价，则称B是A的关于决策D的正域约简。
在上述例子中基于X1：令B1={L，I},则B1的正域为{e3，e4，e5，e8}
令B2={L，P}，则B2的正域为{e1,e2,e3,e4,e5,e8}
B3={L,I},则B3的正域为{e1,e2,e3,e4,e5}
可见只有B2满足第一个条件，
且L的正域={e8}
P的正域={e1,e2,e3,e4,e5}
故B2={L，P}即为A={L,I,P}下的基于决策X1的正域约简。
5.负域、边界域以及相关的约简
5.1负域：与普通粗糙集不同，多粒度粗糙集的负域是所有不同决策属性上近似的补集的交集,记为: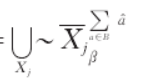
,其中B为变精度。
如上例子中，负域为X1上近似 的补集 U X2上近似的补集=Ø。
5.2负域的约简：
与正域的约简类似，在属性集中若B属于A，且B的负域与A的负域等价，同时满足C属于B，且C的负域与A的负域不等价，则称B是A的关于决策D的负域约简。
在上述例子中基于X1：令B1={L，I},则B1的负域为Ø
令B2={L，P}，则B2的负域为Ø
B3={L,I},则B3的负域为Ø
可见三者都满足第一个条件，
且L的负域为Ø
I的负域为Ø
P的负域为Ø
故{L}，{I}，{P}即为A={L,I,P}下的基于决策X1的负域的约简。
5.3边界域：与普通粗糙集不同，多粒度粗糙集的边界域是所有不同决策属性上近似减去下近似的交集,记为：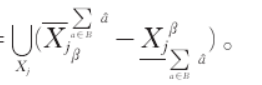
,其中B为变精度。
如上例子中，边界域为X1上近似-X1的下近似 U X2上近似-X2的下近似=U。
5.4边界域的约简：在属性集中若B属于A，且B的边界域与A的边界域等价，同时满足C属于B，且C的边界域与A的边界域不等价，则称B是A的关于决策D的边界域约简。
在上述例子中基于X1：令B1={L，I},则B1的边界域为U
令B2={L，P}，则B2的边界域为U
B3={L,I},则B3的边界域为{e1,e2,e6,e7,e8}
可见B1,B2满足第一个条件，
且L的边界域为{e1,e2,e3,e4,e5,e6,e7}
I的边界域为{e1,e2,e6,e7,e8}
P的边界域为{e6,e7,e8}
故{L,I},{L,P}即为A={L,I,P}下的基于决策X1的边界域的约简。
