【补充】二项树与二项堆
二项树
二项树 B k B_k Bk 是一种递归定义的有序树。如下图所示，二项树 B 0 B_0 B0 只包含一个结点，二项树 B k B_k Bk 由两棵二项树 B k − 1 B_{k-1} Bk−1 连接而成：其中一棵树的根是另一棵树的根的最左孩子。
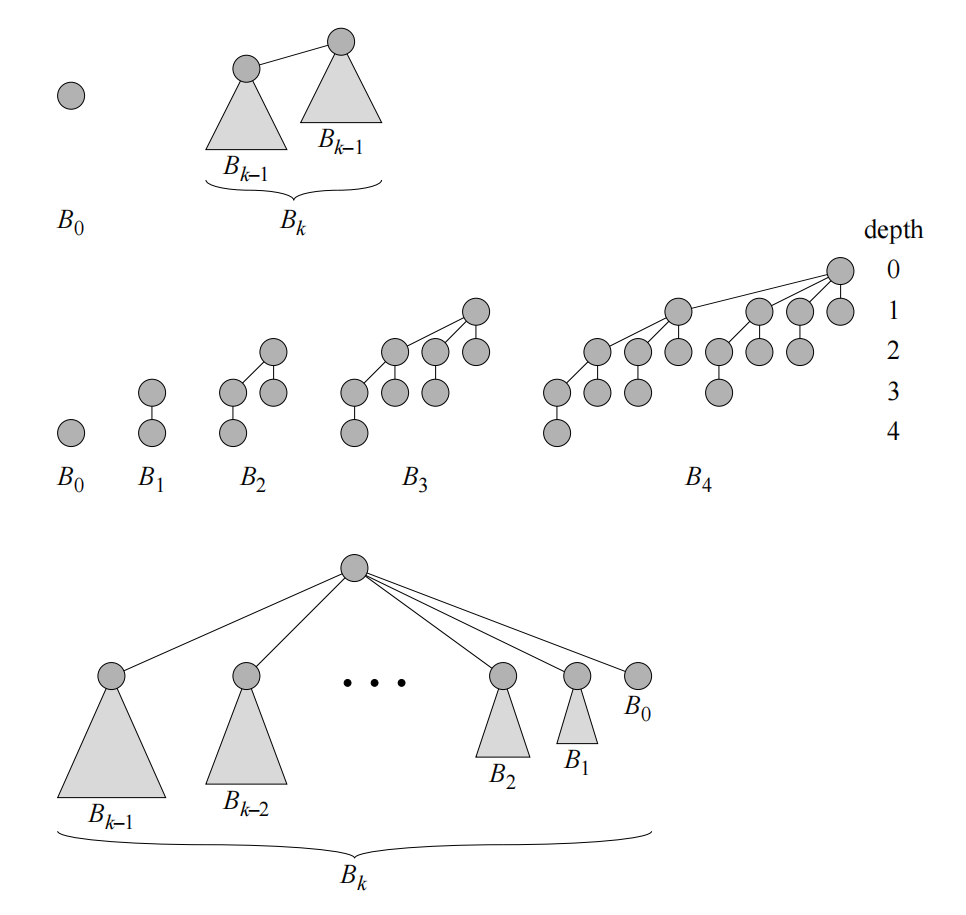
二项树 B k B_k Bk 的性质：
- 共有 2 k 2^k 2k 个结点。
- 树的高度为 k k k。
- 在深度 i i i 处恰有 C k i C_k^i Cki 个结点，其中 i = 0 , 1 , 2 , ⋯ , k i=0, 1, 2, \cdots, k i=0,1,2,⋯,k。
- 根的度数为 k k k，它大于任何其他结点的度数；并且，如果根的子女从左到右编号为 k − 1 , k − 2 , ⋯ , 0 k-1, k-2, \cdots, 0 k−1,k−2,⋯,0，子女 i i i 是子树 B i B_i Bi 的根。
推论：在一棵包含 n n n 个结点的二项树中，任意结点的最大度数为 log n \log n logn。
二项堆
二项堆 H H H 由一组满足下面二项堆性质的二项树组成。
- H H H 中的每个二项树遵循最小堆性质，即结点的关键字大于或等于其父结点的关键字。我们称这种树是最小堆有序的。
- 对任意非负整数 k k k，在 H H H 中至多有一棵二项树的根具有度数 k k k。
二项堆 H H H 最多包含 ⌊ log n ⌋ + 1 \lfloor \log n \rfloor+1 ⌊logn⌋+1 棵二项树。
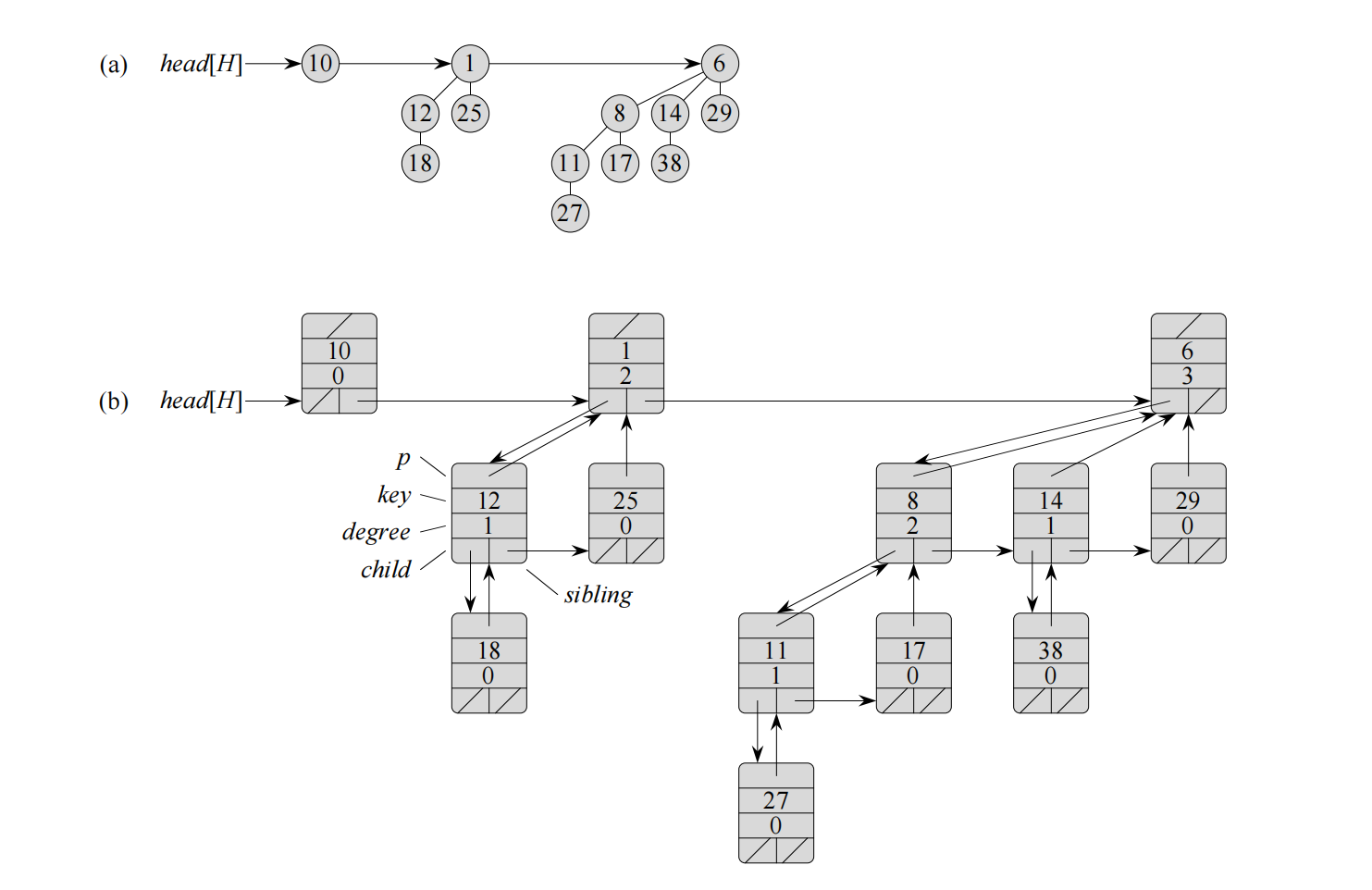
上图为一个包含13个结点的二项堆。（a）一个二项堆包含了二项树 B 0 , B 2 , B 3 B_0, B_2, B_3 B0,B2,B3，它们分别由1个、4个、8个结点，即共有13个结点。由于每棵二项树都是最小堆有序的，所以任意结点的关键字都不小于其父结点的关键字。图中还标记出了根链，它是一个按根的度数递增排序的链表。（b）二项堆 H H H 的一个更具体的表示，每棵二项树按左孩子、右兄弟表示方式存储，每个结点还存储自身的度数。
合并两个二项堆
下面的过程合并二项堆
H
1
H_1
H1 和
H
2
H_2
H2，并返回结果堆。在合并过程中也破坏了
H
1
H_1
H1 和
H
2
H_2
H2。过程中使用了一个辅助过程BINOMIAL-HEAP-MERGE，将
H
1
H_1
H1 和
H
2
H_2
H2 的根链表合并成一个按度数单调递增的链表。BINOMIAL-HEAP-MERGE过程与归并排序的过程类似。
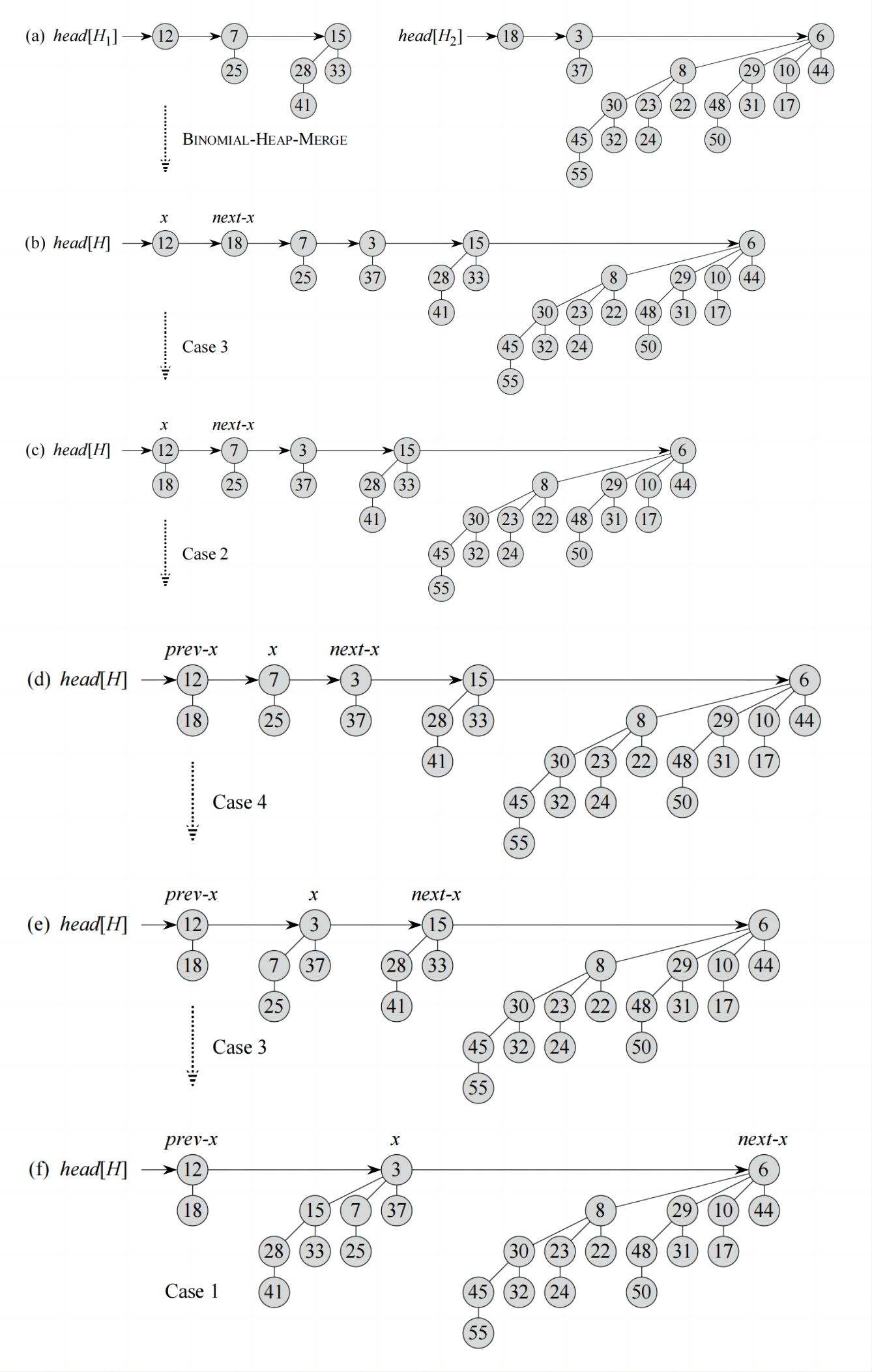
BINOMIAL-HEAP-UNION的运行时间为 O ( log n ) \Omicron(\log n) O(logn)。
二项堆的应用
- 最小生成树算法
- Kruskal算法
- Prim算法
- 最短路径算法
- Dijkstra算法
