算法导论-第33章-最近点对问题
最近点对问题
问题描述:在 \(n \ge 2\) 个点的集合 \(Q\) 中寻找最近点对的问题,“最近”指的是欧几里得距离最小,即点 \(p_1=(x_1, y_1)\) 和 \(p_2=(x_2, y_2)\) 之间的欧几里得距离 \(d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) 最小。集合 \(Q\) 中的两个点可能会重合,这种情况下,它们之间的距离为0。
现实应用:最近点对问题可以应用于交通控制系统中。为检测出潜在的碰撞事故,在空中或海洋交通控制系统中,需要识别出两个距离最近的交通工具。
求平面上\(n\)个顶点的最近点对问题,对文件data.txt的所有点,求距离最近的点对及其距离。
输入:字符串文件data.txt。每行三个数,分别表示顶点编号和其横纵坐标。
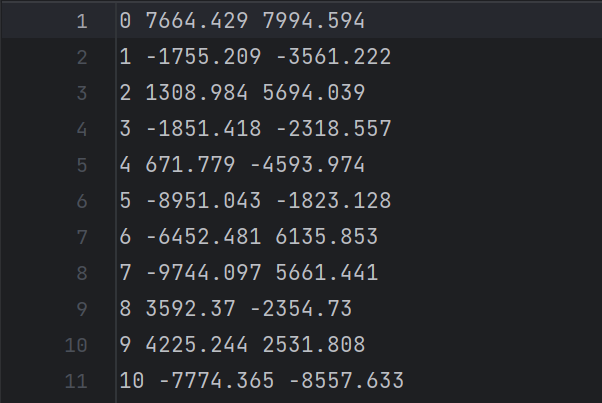
输出:输出距离最近的一对顶点编号,及其距离值。
暴力法
遍历所有点,计算两点之间的距离。如果当前点对之间的距离更小,则更新距离最近的点对信息。
分治法
算法思想:
分治算法的每一次递归调用的输入为子集 \(P\subseteq Q\) 以及数组 \(X\) 和 \(Y\),数组 \(X\) 和 \(Y\) 均包含 \(P\) 中的所有点。按照 \(x\) 坐标单调递增的方式对数组 \(X\) 中的点排序,按照 \(y\) 轴坐标单调递增的方式对数组 \(Y\) 中的点排序。
输入为 \(P\)、\(X\) 和 \(Y\) 的递归调用首先检查是否有 \(|P|\le3\) 成立。如果成立,则执行暴力法,求 \(\begin{pmatrix} |P| \\ 2 \end{pmatrix}\\\) 个点对中的最近点对;如果不成立,则递归调用如下分治法。
递归法三步骤:
分解(Divide):找出一条垂直线 \(l\),垂直线 \(l\) 满足能够将点集 \(P\) 分为两部分 \(P_L\) 和 \(P_R\) :使得 \(|P_L|=\lceil|P|/2\rceil,|P_R|=\lfloor|P|/2\rfloor\),即两部分点的个数之差不超过 1。\(P_L\) 中所有的点都在直线 \(l\) 上或在 \(l\) 的左侧,\(P_R\) 中所有的点都在直线 \(l\) 上或在 \(l\) 的右侧。数组 \(X\) 被划分为两个数组 \(X_L\) 和 \(X_R\),分别包含 \(P_L\) 和 \(P_R\) 中的点,并按 \(x\) 轴坐标单调递增的方式排序。类似地,将数组 \(Y\) 划分为两个数组 \(Y_L\) 和 \(Y_R\),分别包含 \(P_L\) 和 \(P_R\) 中的点,并按 \(y\) 轴坐标单调递增的方式排序。
解决(Conquer):把 \(P\) 划分为 \(P_L\) 和 \(P_R\) 后,再进行两次递归调用,一次找出 \(P_L\) 中的最近点对,另一次找出 \(P_R\) 中的最近点对。第一次调用的输入为子集 \(P_L\)、数组 \(X_L\) 和 \(Y_L\);第二次调用的输入为子集 \(P_R\)、\(X_R\) 和 \(Y_R\)。令 \(P_L\) 和 \(P_R\) 返回的最近点对的距离分别为 \(\delta_L\) 和 \(\delta_R\),并且置 \(\delta=min(\delta_L, \delta_R)\)。
合并(Combine):最近点对要么是某次递归找出距离为 \(\delta\) 的点对,要么是 \(P_L\) 中的一个点和 \(P_R\) 中的一个点组成的点对。如果存在这样的一个点,则点对中的两个点于直线 \(l\) 的距离必定都在 \(\delta\) 之内。因此,它们必定都处于以直线 \(l\) 为中心、宽度为 \(2\delta\) 的垂直带型区域内。为了找出这样的点对(如果存在),算法要做如下工作:
- 建立一个数组 \(Y'\),它是把数组 \(Y\) 中所有不在宽度为 \(2\delta\) 的垂直带型区域内的点去掉后所得的数组。数组 \(Y'\) 与 \(Y\) 一样,是按 \(y\) 轴坐标排序的。
- 对数组 \(Y'\) 中的每一个点 \(p\),算法试图找出距离 \(p\) 在 \(\delta\) 以内的点。在 \(Y'\)中仅需考虑紧随 \(p\) 后的7个点。算法计算出从 \(p\) 到这7个点的距离,并记录下 \(Y'\) 的所有点对中最近点对的距离 \(\delta'\)。
- 返回 \(\delta\) 和 \(\delta'\) 中较小的那个距离以及对应的点对。
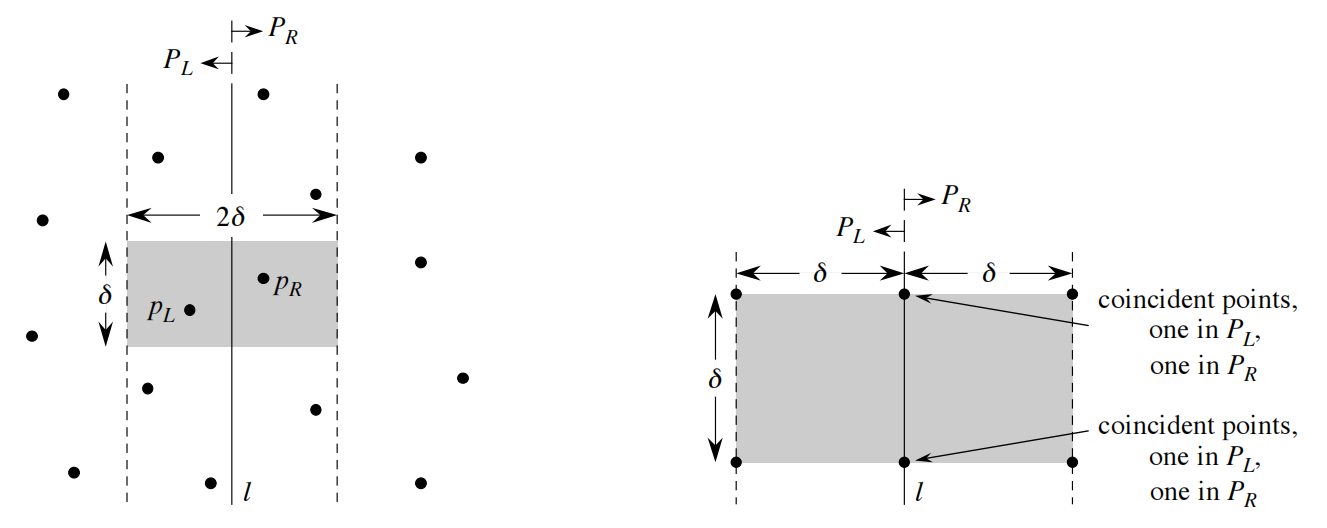
代码实现:
代码中封装了两个类,一个是Point,记录的是点的信息,包括编号、\(x\) 轴坐标、\(y\) 轴坐标;另一个是PointResult,记录的是最近点对信息,包括两个Point和它们之间的距离diastance。
在Point类中,还实现了按照 \(x\) 轴坐标和 \(y\) 轴坐标对Point对象进行定制排序。
在主类FindTheClosestPointPair中,实现了三个方法,分别是计算欧几里得距离、暴力法求最近点对和分治法求最近点对。
- 计算欧几里得距离:直接按照\(d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)定义计算。
- 暴力法:遍历所有情况,求 \(\begin{pmatrix} |P| \\ 2 \end{pmatrix}\\\) 个点中的最近点对。
- 分治法:先按 \(x\) 轴坐标进行定制排序。点集中点的个数小于或等于3,则直接使用暴力法求解最近点对,保存到
PointResult,这也是递归的出口。否则,从中间将点集分为两部分,递归地求解左右两部分。但是要考虑最近点对中的点是一个在垂直线左侧,一个在垂直线上或垂直线右侧的情况。- 遍历范围内的点,找出在以垂直线为中心,宽度为
2*PointResult.distance范围内的所有点; - 按 \(y\) 轴坐标进行定制排序;
- 对于垂直带型区域内的某个点,计算所有和它 \(y\) 轴坐标相差不超过
PointResult.distance的点距,如果有比之前PointResult中记录小的点距,就更新PointResult。
- 遍历范围内的点,找出在以垂直线为中心,宽度为
Java代码实现:
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.Paths;
import java.util.*;
/**
* 将点的信息(编号、横坐标、纵坐标)封装为Point类
*/
class Point {
private int number;
private double x;
private double y;
public Point() {
}
public Point(int number, double x, double y) {
this.number = number;
this.x = x;
this.y = y;
}
public int getNumber() {
return number;
}
public void setNumber(int number) {
this.number = number;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x = x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y = y;
}
/**
* 按照x轴坐标单调递增进行定制排序
* @param points
* @return Point[]
*/
public static Point[] compareX(Point[] points) {
Arrays.sort(points, (o1, o2) -> (int) (o1.getX() - o2.getX()));
return points;
}
/**
* 按照y轴坐标单调递增定制排序
* @param points
* @return Point[]
*/
public static Point[] compareY(Point[] points) {
Arrays.sort(points, (o1, o2) -> (int) (o1.getY() - o2.getY()));
return points;
}
@Override
public String toString() {
return "Point{" +
"number=" + number +
", x=" + x +
", y=" + y +
'}';
}
}
/**
* 将要返回的结果封装为一个点对类,包括两个点,以及距离
*/
class PointResult{
private Point p1;
private Point p2;
private double distance;
public PointResult() {
}
public PointResult(Point p1, Point p2, double distance) {
this.p1 = p1;
this.p2 = p2;
this.distance = distance;
}
public Point getP1() {
return p1;
}
public void setP1(Point p1) {
this.p1 = p1;
}
public Point getP2() {
return p2;
}
public void setP2(Point p2) {
this.p2 = p2;
}
public double getDistance() {
return distance;
}
public void setDistance(double distance) {
this.distance = distance;
}
@Override
public String toString() {
return "PointResult{" +
"p1=" + p1 +
", p2=" + p2 +
", distance=" + distance +
'}';
}
}
public class FindTheClosestPointPair {
/**
* 计算两个点之间的欧几里得距离
* @param p1
* @param p2
* @return distance
*/
public static double distance(Point p1, Point p2) {
return Math.sqrt((p1.getX() - p2.getX()) * (p1.getX() - p2.getX()) + (p1.getY() - p2.getY()) * (p1.getY() - p2.getY()));
}
/**
* 寻找最近点对(暴力解法)
* @param points
* @param left
* @param right
* @return PointResult
*/
public static PointResult violentSolution(Point[] points, int left, int right) {
PointResult pointResult = new PointResult();
pointResult.setDistance(Double.MAX_VALUE);
for (int i = left; i < right; i++) {
for (int j = i + 1; j < right; j++) {
double dis = distance(points[i], points[j]);
if (dis < pointResult.getDistance()) {
pointResult.setDistance(dis);
pointResult.setP1(points[i]);
pointResult.setP2(points[j]);
}
}
}
return pointResult;
}
/**
* 寻找最近点对(分治法)
* @param points
* @param left
* @param right
* @return PointResult
*/
public static PointResult divideAndConquer(Point[] points, int left, int right) {
PointResult pointResult = null;
if (right - left <= 3) { // 当点数小于3的时候,直接使用暴力解法求最近点对
return violentSolution(points, left, right);
}
int mid = (left + right) / 2; // 分治(从中点分开)
PointResult leftPointResult = divideAndConquer(points, left, mid); // 递归计算左部分最近点对
PointResult rightPointResult = divideAndConquer(points, mid, right); // 递归计算右部分最近点对
pointResult = leftPointResult.getDistance() < rightPointResult.getDistance() ? leftPointResult : rightPointResult; // 根据距离判断返回的最近点对是哪个
// 根据上面求得的distance,找出处于以直线l为中心、宽度为2*distance的垂直带型区域内的点集
List<Point> area = new ArrayList<>();
for (int i = left; i < right; i++) {
if (Math.abs(points[i].getX() - points[mid].getX()) < pointResult.getDistance()) {
area.add(points[i]);
}
}
// 对上面垂直带型区域内的点集按照y轴坐标定制排序
Point.compareY(points);
// 遍历垂直带型区域,要求y轴坐标只差不超过pointResult.distance(因为超过了也就没有必要计算欧几里得距离了,必定比之前得到的resultPoint.distance大)
for (int i = 0; i < area.size(); i++) {
for (int j = i + 1; j < area.size() && ((area.get(j).getY() - area.get(i).getY()) < pointResult.getDistance()); j++) {
double dis = distance(area.get(i), area.get(j));
if (dis < pointResult.getDistance()) { // 如果有这样的点对,更新pointResult
pointResult.setDistance(dis);
pointResult.setP1(area.get(i));
pointResult.setP2(area.get(j));
}
}
}
return pointResult;
}
public static void main(String[] args) throws IOException {
// 读取data.txt文件,每一行包含顶点的信息,按空格分割
String path = "C:\\Projects\\IDEAProjects\\algorithms\\src\\main\\java\\ch33\\data.txt";
List<String> readAllLines = Files.readAllLines(Paths.get(path));
Point[] points = new Point[readAllLines.size()];
for (int i = 0; i < points.length; i++) {
String[] line = readAllLines.get(i).split("\\s+");
points[i] = new Point();
points[i].setNumber(Integer.parseInt(line[0]));
points[i].setX(Double.parseDouble(line[1]));
points[i].setY(Double.parseDouble(line[2]));
//System.out.println(points[i]);
}
// 计算算法耗时
long start = System.currentTimeMillis();
//// 暴力解法
//PointResult pointResult = violentSolution(points, 0, points.length);
// 分治法
Point.compareX(points);
PointResult pointResult = divideAndConquer(points, 0, points.length);
long end = System.currentTimeMillis();
System.out.println(pointResult);
System.out.println("算法耗时: " + (end - start) + " ms");
}
}
结果与分析
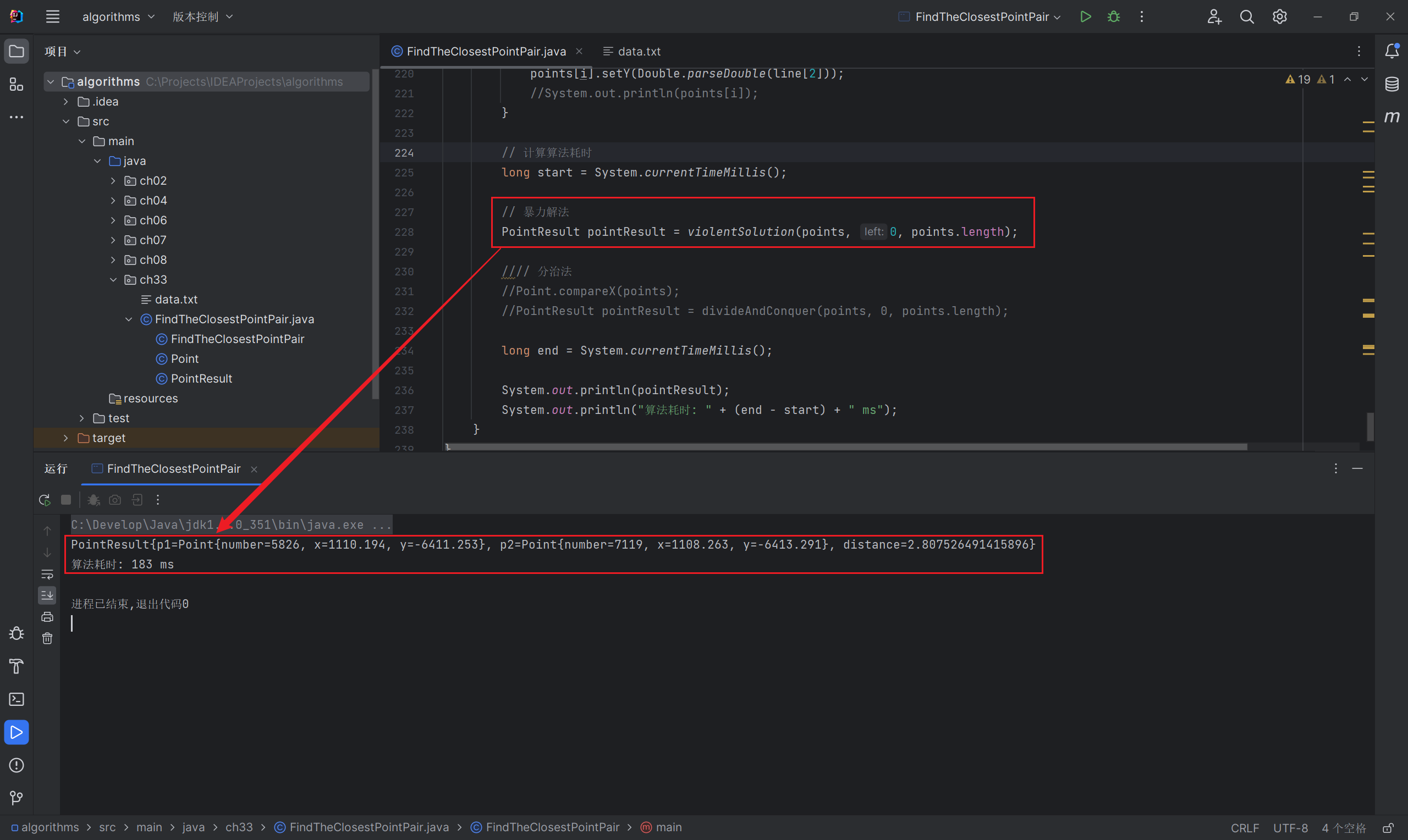
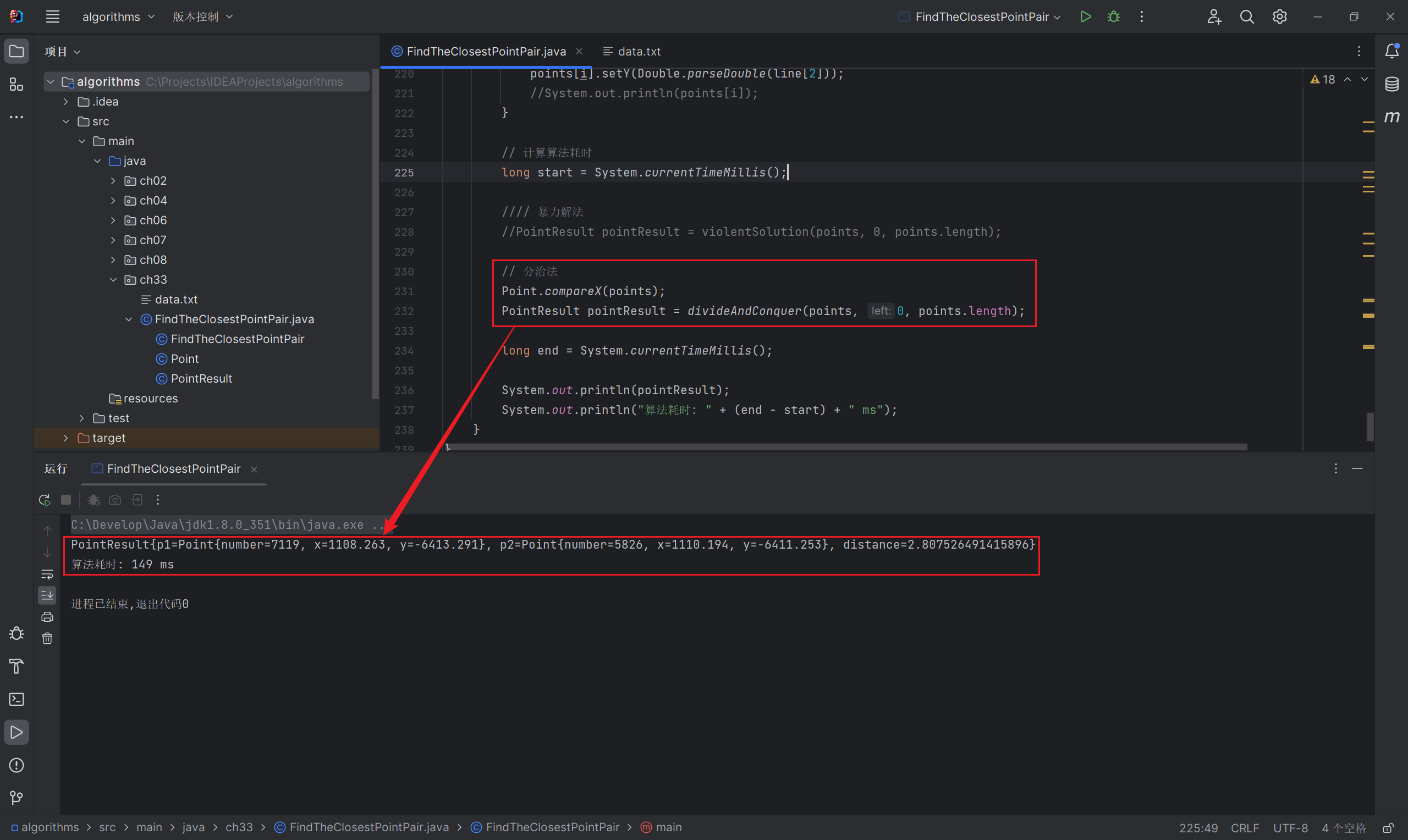
在使用朴素算法(暴力)解决最近点对问题的过程中,只需简单的查看所有 \(\begin{pmatrix} n \\ 2 \end{pmatrix}\\=\Theta(n^2)\) 个点对。而分治算法,其运行时间可以用 \(T(n)=2T(n/2)+\Omicron(n)\) 来描述。因此,该算法的运行时间仅为 \(\Omicron(n \log n)\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号