算法导论-第13章-红黑树
第12章介绍了一棵高度为\(h\)的二叉搜索树,它可以支持任何一种基本动态集合操作,如SEARCH、PREDECESSOR、SUCCESSOR、MINIMUM、MAXIMUM、INSERT和DELETE等,其时间复杂度均为\(\Omicron(h)\)。因此,如果搜素树的高度较低时,这些操作会执行的较快。然而,如果树的高度较高时,这些操作可能不比在链表上执行得快。红黑树(red-black tree)是“平衡”搜索树的一种,可以保证在最坏情况下基本动态集合操作得时间复杂度为\(\Omicron(\log n)\)。
13.1 红黑树的性质
红黑树(Red-Black Tree,RBT)是一棵二叉搜索树,它在每个结点上增加了一个存储位来表示结点的颜色,颜色可以是RED或BLACK。通过对从根到叶的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长2倍,因此是近似平衡的。
红黑树RBT与平衡二叉树AVL比较:AVL树比红黑树更加平衡,但AVL树在插入和删除的时候也会存在大量的旋转操作。所以当你的应用涉及到频繁的插入和删除操作,切记放弃AVL树,选择性能更好的红黑树;当然,如果你的应用中涉及的插入和删除操作并不频繁,而是查找操作相对更频繁,那么就优先选择AVL树进行实现。
树中的每个结点包含5个属性:color、key、left、right和p。如果一个结点没有子结点或父结点,则该结点相应指针属性的值为NIL。我们可以把这些NIL视为指向二叉搜索树的叶结点(外部结点)的指针,而把带关键字的结点视为树的内部结点。
一棵红黑树(如下图a)是满足下面红黑性质的二叉搜索树:
- 每个结点都是红色或黑色
- 根结点是黑色的
- 每个叶结点(NIL)是黑色的
- 如果一个结点是红色,则它的两个子结点都是黑色
- 对每个结点,从该结点到其所有后代结点的简单路径上,均包含相同数目的黑色结点
为了便于处理红黑树代码中的边界条件,使用一个哨兵来代表NIL。对于一棵红黑树 \(T\),哨兵 \(T.nil\) 是color属性为BLACK,而其他属性可以为任意值的结点(如下图b)。
我们通常将注意力放在红黑树的内部结点,因为它们存储了关键字。因此,后续所画的红黑树都忽略了叶结点(如下图c)。
从某个结点 \(x\) 出发(不含该结点)到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的黑高,记为 \(bh(x)\)。红黑树的黑高为根结点的黑高。
引理:一棵有 \(n\) 个内部结点的红黑树的高度最大为 \(2\log{(n+1)}\)。
证明:以 \(x\) 为根结点的子树至少有 \(2^{bh(x)}−1\) 个内部结点。设 \(ℎ\) 为树高,根据性质4, \(bh(x)≥ℎ/2\) ,于是有 \(n≥2^{ℎ/2}−1\) ,变形可得 \(ℎ≤2\log(n+1)\) ,得证。
13.2 旋转
当二叉搜索树的TREE-INSERT和TREE-DELETE操作运行在有 \(n\) 个关键字的红黑树上,运行时间为 \(\Omicron(\log n)\) 。为了维护红黑性质,需要修改树中某些结点的颜色和指针。
指针结构的修改通过旋转(ratation)完成。下图给出了两种旋转:
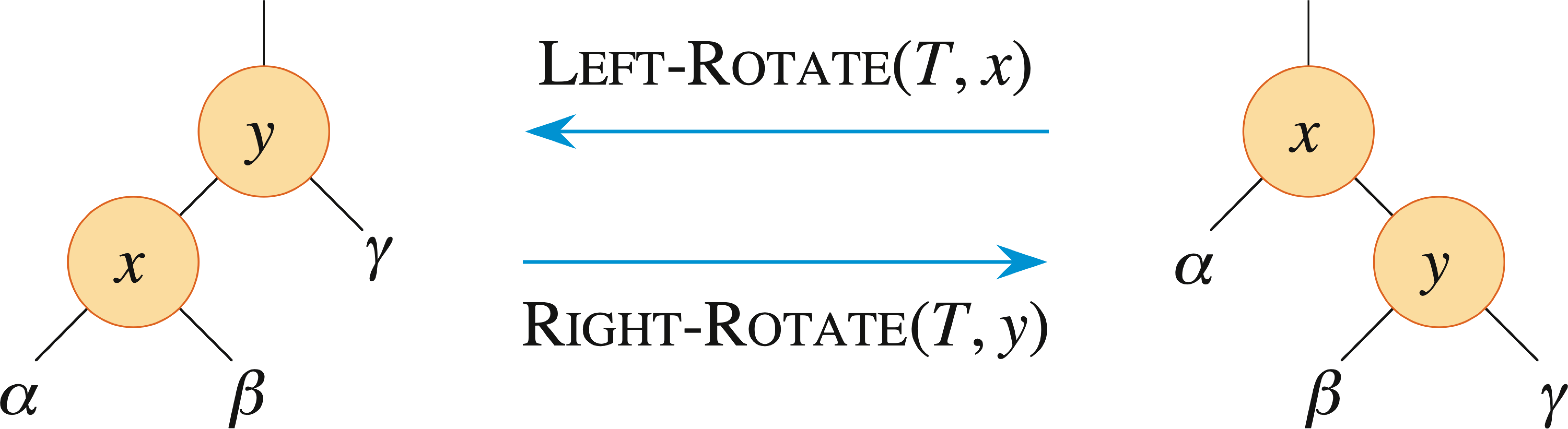
LEFT-ROTATE(T, x)操作通过改变常数数目的指针,可以将右边两个结点的结构转变为左边的结构。左边的结构可以使用RIGHT-ROTATE(T, y)转变为右边的结构。
在LEFT-ROTATE(T, x)的伪代码中,假设 \(x.right \ne T\) 且根结点的父结点为 \(T.nil\)。

左旋操作:主要修改三对指针,如下图所示。右旋同理。
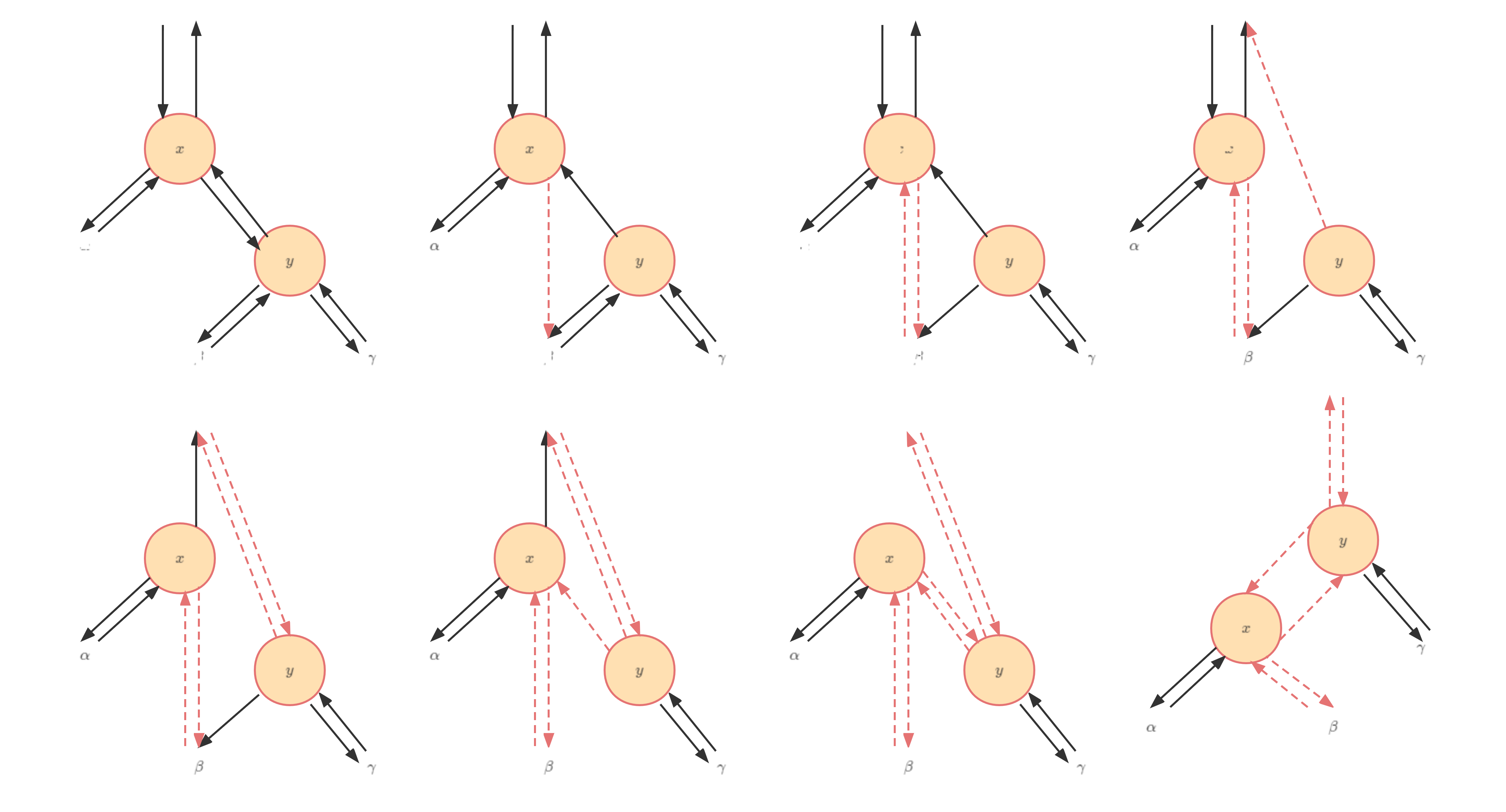
下图给出了LEFT-ROTATE操作修改二叉搜索树的例子。LEFT-ROTATE和RIGHT-ROTATE都在 \(\Omicron(1)\) 时间内完成。在旋转操作中,只有指针改变,其他所有属性都保持不变。
13.3 插入
插入操作可以在 \(\Omicron(\log n)\) 时间内完成。红黑树的插入操作通过两步来完成:
- 插入结点:首先将其按照二叉搜索树的规则插入到合适的位置上;新结点被插入时,将其颜色设置为红色。
- 调整结点颜色和结构(维持红黑树的性质):插入结点后,可能会破坏红黑树的性质,需要调整结点的颜色和结构来维护红黑树的性质,有6种情况,见代码。
RB-INSERT的核心思想与二叉搜索树的相同:首先,从根结点向下遍历,根据关键字大小比较是该插入在左子树还是右子树,同时设置 \(y\) 保存待插入结点的父结点;然后,判断待插入结点是 \(y\) 的左子树还是右子树(注意判断是否为空树);最后,给待插入结点的其他属性赋值(颜色为红色)。

RB-INSERT-FIXUP的核心思想:分情况讨论,见代码......🤣




编码实现红黑树的插入算法,使得插入后依旧保持红黑性质。
输入:文件名 insert.txt,第一行为待插入数据的个数,第二行为待插入的数据(int 类型, 空格分割)
输出:将插入完成后的红黑树进行 “先序遍历(NLR)” , “中序遍历(LNR)”和“层次遍历(Level-Order Traverse)” 并将相应的遍历序列输出到文件中。
import java.io.BufferedWriter;
import java.io.File;
import java.io.FileWriter;
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.Paths;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
/**
* 红黑树颜色枚举类
*/
enum Color {
RED,
BLACK
}
/**
* 红黑树结点类
*/
class Node {
int key; // 关键字
Color color; // 结点颜色
Node left; // 左孩子
Node right; // 右孩子
Node p; // 父结点
/**
* 构造器
*
* @param key 关键字
*/
public Node(int key) {
this.key = key;
this.color = Color.RED;
this.left = null;
this.right = null;
this.p = null;
}
/**
* 全参构造器
*
* @param key 关键字
* @param color 结点颜色
* @param left 左孩子
* @param right 右孩子
* @param p 父结点
*/
public Node(int key, Color color, Node left, Node right, Node p) {
this.key = key;
this.color = color;
this.left = left;
this.right = right;
this.p = p;
}
}
/**
* 红黑树类
*/
public class RBTree {
private Node root;
private Node nil; // 哨兵
/**
* 构造器
*/
public RBTree() {
nil = new Node(-1, Color.BLACK, null, null, null);
root = nil;
}
/**
* 1、先按照二叉搜索树的规则插入结点
*
* @param key 结点的关键字,根据关键字构造出插入的结点
*/
public void insert(int key) {
Node node = new Node(key);
Node y = nil;
Node x = root;
while (x != nil) {
y = x;
if (node.key < x.key) {
x = x.left;
} else {
x = x.right;
}
}
node.p = y;
if (y == nil) {
root = node;
} else if (node.key < y.key) {
y.left = node;
} else {
y.right = node;
}
node.left = nil;
node.right = nil;
node.color = Color.RED;
insertFix(node);
}
/**
* 2、调整结点颜色和结构(维持红黑树的性质)
*
* @param z 待插入的结点
*/
public void insertFix(Node z) {
Node y;
while (z.p.color == Color.RED) {
if (z.p == z.p.p.left) { // z的父节点是一个左孩子?
y = z.p.p.right; // y是z的叔结点
if (y.color == Color.RED) { // z的父结点和叔结点都是红色?
z.p.color = Color.BLACK; // case 1
y.color = Color.BLACK; // case 1
z.p.p.color = Color.RED; // case 1
z = z.p.p; // case 1
System.out.println("case 1: z的父结点是左孩子,z的父结点和叔结点都是红色");
} else {
if (z == z.p.right) { // z的叔结点y是黑色且z是一个右孩子
z = z.p; // case 2
leftRotate(z); // case 2
System.out.println("case 2: z的父结点是左孩子,z的父结点是红色,z的叔结点y是黑色,z是一个右孩子");
}
// z的叔结点y是黑色且z是一个左孩子
z.p.color = Color.BLACK; // case 3
z.p.p.color = Color.RED; // case 3
rightRotate(z.p.p); // case 3
System.out.println("case 3: z的父结点是左孩子,z的父结点是红色,z的叔结点y是黑色,z是一个左孩子");
}
} else { // z的父节点是一个右孩子?
y = z.p.p.left; // y是z的叔结点
if (y.color == Color.RED) { // z的父结点和叔结点都是红色?
z.p.color = Color.BLACK; // case 4
y.color = Color.BLACK; // case 4
z.p.p.color = Color.RED; // case 4
z = z.p.p; // case 4
System.out.println("case 4: z的父结点是右孩子,z的父结点和叔结点都是红色");
} else {
if (z == z.p.left) { // z的叔结点y是黑色且z是一个左孩子
z = z.p; // case 5
rightRotate(z); // case 5
System.out.println("case 5: z的父结点是右孩子,z的父结点是红色,z的叔结点y是黑色,z是一个左孩子");
}
// z的叔结点y是黑色且z是一个左孩子
z.p.color = Color.BLACK; // case 6
z.p.p.color = Color.RED; // case 6
leftRotate(z.p.p); // case 6
System.out.println("case 6: z的父结点是右孩子,z的父结点是红色,z的叔结点y是黑色,z是一个右孩子");
}
}
}
root.color = Color.BLACK;
}
/**
* 左旋
*
* @param x 左旋
*/
public void leftRotate(Node x) {
Node y = x.right;
x.right = y.left;
if (y.left != nil) {
y.left.p = x;
}
y.p = x.p;
if (x.p == nil) {
root = y;
} else if (x == x.p.left) {
x.p.left = y;
} else {
x.p.right = y;
}
y.left = x;
x.p = y;
}
/**
* 右旋
*
* @param x 右旋
*/
public void rightRotate(Node x) {
Node y = x.left;
x.left = y.right;
if (y.right != nil) {
y.right.p = x;
}
y.p = x.p;
if (x.p == nil) {
root = y;
} else if (x == x.p.right) {
x.p.right = y;
} else {
x.p.left = y;
}
y.right = x;
x.p = y;
}
/**
* 先序遍历
*
* @param node 树的根结点
* @param preList 输出集合
*/
public void preOrder(Node node, List<Node> preList) {
if (node == nil) return;
preList.add(node);
preOrder(node.left, preList);
preOrder(node.right, preList);
}
/**
* 中序遍历
*
* @param node 树的根结点
* @param inList 输出集合
*/
public void inOrder(Node node, List<Node> inList) {
if (node == nil) return;
inOrder(node.left, inList);
inList.add(node);
inOrder(node.right, inList);
}
/**
* 层序遍历
*
* @param root 树的根结点
* @return
*/
public List<Node> levelOrder(Node root) {
List<Node> list = new ArrayList<>();
ArrayDeque<Node> queue = new ArrayDeque<>();
if (root != null) queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
Node node = queue.poll();
if (node != nil) list.add(node);
if (node.left != null) queue.offer(node.left);
if (node.right != null) queue.offer(node.right);
}
}
return list;
}
public static void output(String pathResult, StringBuilder stringBuilder) throws IOException {
File file = new File(pathResult);
if (!file.exists()) {
file.createNewFile();
}
FileWriter fileWriter = new FileWriter(file);
BufferedWriter bufferedWriter = new BufferedWriter(fileWriter);
bufferedWriter.write(stringBuilder.toString());
bufferedWriter.close();
}
public static void main(String[] args) throws IOException {
// 读取insert.txt文件中的数据(第一行为数组长度, 第二行为数组(int类型)的内容)
String path = "C:\\Projects\\IDEAProjects\\algorithms\\src\\main\\java\\ch13\\insert.txt";
List<String> readAllLines = Files.readAllLines(Paths.get(path));
int count = Integer.parseInt(readAllLines.get(0));
String[] split = readAllLines.get(1).split("\\s+");
int[] array = new int[count];
for (int i = 0; i < count; i++) {
array[i] = Integer.parseInt(split[i]);
}
// 插入所有结点
RBTree rbTree = new RBTree();
for (int i = 0; i < count; i++) {
System.out.println("======" + i + "======");
rbTree.insert(array[i]);
}
// 先序遍历
ArrayList<Node> preList = new ArrayList<>();
StringBuilder preStringBuilder = new StringBuilder();
rbTree.preOrder(rbTree.root, preList); // 9 4 1 0 2 3 6 5 7 8 14 12 11 10 13 18 16 15 17 19
for (Node node : preList) {
preStringBuilder.append("key = ").append(node.key).append(", color = ").append(node.color).append("\n");
output("C:\\Projects\\IDEAProjects\\algorithms\\src\\main\\java\\ch13\\NLR.txt", preStringBuilder);
//System.out.println("key = " + node.key + ", color = " + node.color);
}
//System.out.println("=================================================");
// 中序遍历
ArrayList<Node> inList = new ArrayList<>();
StringBuilder inStringBuilder = new StringBuilder();
rbTree.inOrder(rbTree.root, inList);
for (Node node : inList) {
inStringBuilder.append("key = ").append(node.key).append(", color = ").append(node.color).append("\n");
output("C:\\Projects\\IDEAProjects\\algorithms\\src\\main\\java\\ch13\\LNR.txt", inStringBuilder);
//System.out.println("key = " + node.key + ", color = " + node.color);
}
//System.out.println("=================================================");
// 层序遍历
List<Node> levelList = rbTree.levelOrder(rbTree.root);
StringBuilder levelStringBuilder = new StringBuilder();
for (Node node : levelList) {
levelStringBuilder.append("key = ").append(node.key).append(", color = ").append(node.color).append("\n");
output("C:\\Projects\\IDEAProjects\\algorithms\\src\\main\\java\\ch13\\LOT.txt", levelStringBuilder);
//System.out.println("key = " + node.key + ", color = " + node.color);
}
}
}
13.4 删除






 浙公网安备 33010602011771号
浙公网安备 33010602011771号