算法导论-第15章-动态规划
动态规划(dynamic programming)的思想是分治思想和解决冗余。
- 与分治法相似的是
- 将原问题分解为若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
- 与分治法不同的是
- 经分解的子问题往往不是相互独立的。若用分治法来解,有些共同部分(子问题或子子问题)被重复计算了很多次。
- 而动态规划算法对每个子子问题只求解一次,将其解保存在一个表格中,从而无需每次求解一个子子问题时都需重新计算。
动态规划方法通常用来求解最优化问题(optimization problem)。这类问题可以有很多可行的解,每个解都有一个值,我们希望寻找具有最优值(最小值或最大值)的解。我们称这样的解为问题的一个最优解(an optimal solution),而不是最优解(the optimal solution),因为可能有多个解都是最优值。
我们通常按如下4步骤来设计一个动态规划算法:
- 刻画一个最优解的结构特征。
- 递归地定义最优解的值(写出动态规划方程)。
- 计算最优解的值,通常采用自底向上的方法。
- 利用计算出的信息构造一个最优解。
步骤1~3是动态规划求解问题的基础。如果我们仅仅需要最优解的一个值,而不是最优解本身,可以忽略步骤4。如果要构造最优解,则必须执行步骤4,步骤3中维护的一些额外信息是构造最优解的基础。
下面将讨论如何用动态规划求解最优解问题。15.1节将讨论如何将长钢条切割成短钢条,使其总价值最高。15.2节将讨论如何使用最少次数的标量乘法计算矩阵链乘。15.3节将讨论适合用动态规划求解的问题应该具备的两个关键特征。15.4节将讨论如何使用动态规划求解两个序列的最长公共子序列。15.5节用动态规划方法解决在已知关键字分布的前提下,如何构造最优二叉搜索树。
15.1 钢条切割
钢条切割问题:给定一段长度为 \(n\) 英寸的钢条和一个价格表 \(p_i(i=1, 2, 3, \cdots, n)\)。求切割钢条的方案,使得销售收益 \(r_n\) 最大。注意,如果长度为 \(n\) 英寸的钢条的价格 \(p_n\) 足够大,最优解可能就是完全不需要切割。
假设Serling公司出售一段长度为 \(i\) 英寸的钢条的价格为 \(p_i\)。钢条的长度均为整英寸,价格表如下:
| 长度 \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 价格 \(p_i\) | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
考虑 \(n=4\) 的情况。下图给出了4英寸钢条所有可能的切割方案,包括根本不切割的方案。最优解为方案c。
长度为 \(n\) 的钢条有 \(2^{n-1}\) 种不同的切割方案,因为在距离钢条左端 \(i(i=1,2,\cdots,n-1)\)英寸处,都有切割或不切割两种选择。
如果一个最优解将钢条切割为 \(k(1 \le k \le n)\) 段,那么最优切割方案
最大收益为
一般地,对于\(r_n(n \ge1)\),可以用更短的钢条的最优切割收益来描述它:
其中 \(p_n\) 表示不切割,其他参数对应切割为长度为 \(i\) 和 \(n-i\) 的两段,接着求这两段短钢条的最优收益 \(r_i\) 和 \(r_{n-i}\)。由于无法预知哪种划分方案会获得最大收益,需要遍历所有可能的 \(i\),选取其中收益最大者。
15.4 最长公共子序列
[轻松掌握动态规划]5.最长公共子序列 LCS_哔哩哔哩_bilibili
子序列(subsequence):给定一个序列 \(X=<x_1, x_2, \cdots, x_m>\),另一个序列 \(Z=<z_1, z_2, \cdots, z_k>\),存在一个严格递增的 \(X\) 的下标序列 \(<i_1, i_2, \cdots, i_k>\),对所有 \(j=1,2,\cdots,k\),满足 \(x_{i_j}=z_j\)。例如,\(Z=<B, C, D, B>\)是 \(X=<A, B, C, B, D, A, B>\)的子序列,对应的下标序列为 \(<2, 3, 5, 7>\)。
公共子序列(common subsequence):给定两个序列 \(X\) 和 \(Y\),如果 \(Z\) 既是 \(X\) 的子序列,也是 \(Y\) 的子序列,我们称它是 \(X\) 和 \(Y\) 的公共子序列。例如,\(X=<A, B, C, B, D, A, B>\),\(Y=<B, D, C, A, B, A>\),那么序列 \(<B, C, A>\) 就是 \(X\) 和 \(Y\) 的公共子序列,但不是最长的公共子序列(LCS),因为它的长度为3;而 \(<B, C, B, A>\) 也是 \(X\) 和 \(Y\) 的公共子序列,其长度为4。\(<B, C, B, A>\) 是 \(X\) 和 \(Y\) 的最长公共子序列,\(<B, D, A, B>\) 也是最长公共子序列,因为 \(X\) 和 \(Y\) 不存在长度大于等于5的公共子序列。
最长公共子序列问题(longest-common-subsequence problem):给定两个序列 \(X=<x_1, x_2, \cdots, x_m>\) 和 \(Y=<y_1, y_2, \cdots, y_n>\),求 \(X\) 和 \(Y\) 的最长公共子序列。
步骤1:刻画最长公共子序列的特征
定理:LCS的最优子结构
令 \(X=<x_1, x_2, \cdots, x_m>\) 和 \(Y=<y_1, y_2, \cdots, y_n>\) 为两个序列, \(Z=<z_1, z_2, \cdots, z_k>\) 为 \(X\) 和 \(Y\) 的任意LCS。
- 如果 \(x_m=y_n\),则 \(z_k=x_m=y_n\) 且 \(Z_{k-1}\) 是 \(X_{m-1}\) 和 \(Y_{n-1}\) 的一个 LCS。
- 如果 \(x_m \ne y_n\) 且 \(z_k \ne x_m\),那么 \(Z\) 是 \(X_{m-1}\) 和 \(Y\) 的一个 LCS。
- 如果 \(x_m \ne y_n\) 且 \(z_k \ne y_n\),那么 \(Z\) 是 \(X\) 和 \(Y_{n-1}\) 的一个 LCS。
步骤2:一个递归解
根据LCS的最优子结构定理可知,在求 \(X=<x_1, x_2, \cdots, x_m>\) 和 \(Y=<y_1, y_2, \cdots, y_n>\) 的一个LCS时,我们需要求解一个或两个子问题。如果 \(x_m=y_n\),我们应该求解 \(X_{m-1}\) 和 \(Y_{n-1}\) 的一个LCS,将 \(x_m=y_n\) 追加到这个LCS的末尾,就得到 \(X\) 和 \(Y\) 的一个LCS。如果 \(x_m \ne y_n\),我们必须求解两个子问题:求 \(X_{m-1}\) 和 \(Y\) 的一个 LCS 与 \(X\) 和 \(Y_{n-1}\) 的一个 LCS。两个LCS中较长者即为 \(X\) 和 \(Y\) 的一个LCS。
根据LCS的最优子结构性质,可得如下公式:
步骤3:计算LCS的长度
LCS问题有 \(\Theta(mn)\) 个不同的子问题,可以采用自底向上动态规划进行计算。
LCS-LENGTH过程接受两个序列 \(X=<x_1, x_2, \cdots, x_m>\) 和 \(Y=<y_1, y_2, \cdots, y_n>\) 作为输入。将 \(c[i,j]\) 的值保存在表 \(c[0..m, 0..n]\) 中,并按照行主次序(row-major order)计算表项(即首先从左到右计算 c 的第一行,然后计算第二行,以此类推)。过程中还维护了一个表 \(b[1..m, 1..n]\),帮助构造最优解。
LCS-LENGTH(X, Y, m, n)
let b[1 : m, 1 : n] and c[0 : m, 0 : n] be new tables
for i = 1 to m
c[i, 0] = 0
for j = 0 to n
c[0, j] = 0
for i = 1 to m // compute table entries in row-major order
for j = 1 to n
if x_i == y_j
c[i, j] = c[i - 1, j - 1] + 1
b[i, j] = "↖"
else if c[i - 1, j] ≥ c[i, j - 1]
c[i, j] = c[i - 1, j]
b[i, j] = "↑"
else c[i, j] = c[i, j - 1]
b[i, j] = "←"
return c and b
下图显示了LCS-LENGTH对输入序列 \(X=<A, B, C, B, D, A, B>\) 和 \(Y=<B, D, C, A, B, A>\) 计算的结果。运行时间为 \(\Theta(mn)\),因为每个表项的计算时间为 \(\Theta(1)\)。
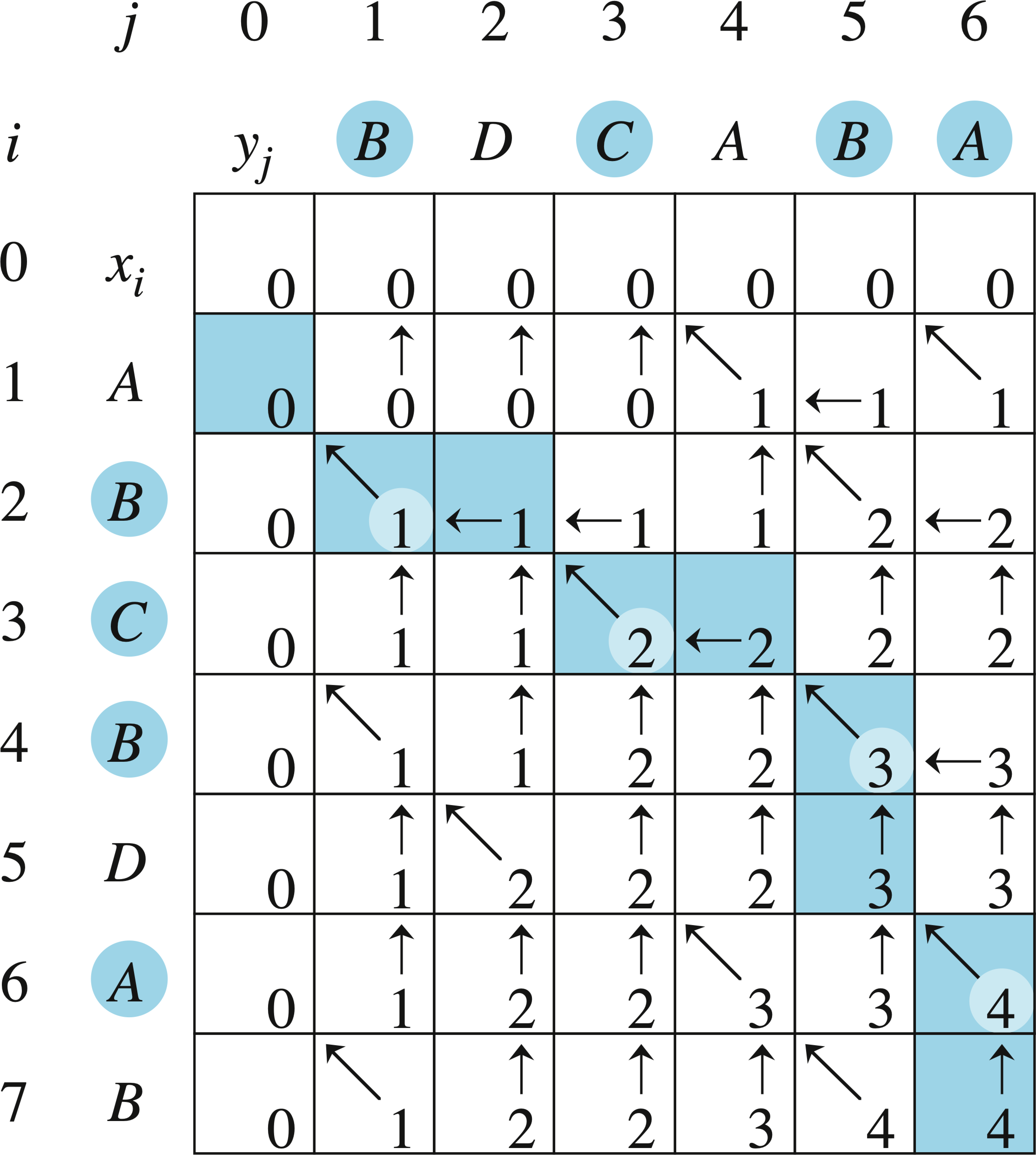
步骤4:构造LCS
要构造LCS,只需从 \(b[m, n]\) 开始,按箭头追踪下去即可。当在表项中遇到”↖“时,意味着 \(x_i=y_j\) 是LCS的一个元素。按照这种方法,就可以依次构造出LCS的所有元素。
PRINT-LCS(b, X, i, j)
if i == 0 or j == 0
return // the LCS has length 0
if b[i, j] == "↖"
PRINT-LCS(b, X, i - 1, j - 1)
print x_i // same as y_i
else if b[i, j] == "↑"
PRINT-LCS(b, X, i - 1, j)
else PRINT-LCS(b, X, i, j - 1)
PRINT-LCS(b, X, m, n)
也可以不依赖表 b。每个 \(c[i, j]\) 项只依赖于表 c 中的其他三项:\(c[i-1, j]、c[i, j-1]、c[i-1, j-1]\)。这种方法节省了 \(\Theta(mn)\) 的空间。此时的空间复杂度是 \(\Theta(mn)\)。
对空间复杂度进行优化
使用滚动数组对空间复杂度进行优化。




LCS的代码实现
编程实现最长公共子序列(LCS)算法,并理解其核心思想。
- 时间复杂度\(\Omicron(mn)\),空间复杂度 \(\Omicron(mn)\),求出LCS及其长度。
- 时间复杂度 \(\Omicron(mn)\),空间复杂度 \(\Omicron(2 * min(m, n))\),求出LCS的长度。
- 时间复杂度 \(\Omicron(mn)\),空间复杂度 \(\Omicron(min(m, n))\),求出LCS的长度。
输入:由控制台输入两个字符串text1,text2。
输出:控制台打印LCS的长度及相应的序列,如不存在公共子序列则返回0.
package ch15;
import java.util.Scanner;
public class LCS {
/**
* 最长公共子序列,空间复杂度O(mn)
* @param seq1 序列1
* @param seq2 序列2
* @return LCS及其长度
*/
public static String longestCommonSubsequence(String seq1, String seq2) {
int m = seq1.length();
int n = seq2.length();
// 创建一个二维数组来保存子问题的解
int[][] dp = new int[m + 1][n + 1];
// 动态规划求解最长公共子序列
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// 从二维数组的右下角开始回溯,构造最长公共子序列
StringBuilder lcs = new StringBuilder();
int i = m, j = n;
while (i > 0 && j > 0) {
if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
lcs.insert(0, seq1.charAt(i - 1));
i--;
j--;
} else if (dp[i - 1][j] > dp[i][j - 1]) {
i--;
} else {
j--;
}
}
return lcs.toString();
}
/**
* 最长公共子序列,空间复杂度2 * O(min(m, n))
* @param seq1 序列1
* @param seq2 序列2
* @return LCS长度
*/
public static int longestCommonSubsequencesPro(String seq1, String seq2) {
int m = seq1.length();
int n = seq2.length();
// 确保 n 是较小的值,以减小空间复杂度
if (m < n) {
String temp = seq1;
seq1 = seq2;
seq2 = temp;
int tempLength = m;
m = n;
n = tempLength;
}
// 创建两行滚动数组来保存子问题的解
int[][] dp = new int[2][n + 1];
// 动态规划求解最长公共子序列的长度
for (int i = 1; i <= m; i++) {
int currRow = i % 2;
int prevRow = (i - 1) % 2;
for (int j = 1; j <= n; j++) {
if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
dp[currRow][j] = dp[prevRow][j - 1] + 1;
} else {
dp[currRow][j] = Math.max(dp[prevRow][j], dp[currRow][j - 1]);
}
}
}
return dp[m % 2][n];
}
/**
* 最长公共子序列,空间复杂度O(min(m, n))
* @param seq1 序列1
* @param seq2 序列2
* @return LCS长度
*/
public static int longestCommonSubsequenceLengthUltra(String seq1, String seq2) {
int m = seq1.length();
int n = seq2.length();
// 确保 n 是较小的值,以减小空间复杂度
if (m < n) {
String temp = seq1;
seq1 = seq2;
seq2 = temp;
int tempLength = m;
m = n;
n = tempLength;
}
// 创建一维数组来保存子问题的解
int[] dp = new int[n + 1];
// 动态规划求解最长公共子序列的长度
for (int i = 1; i <= m; i++) {
int prev = 0;
for (int j = 1; j <= n; j++) {
int current = dp[j];
if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
dp[j] = prev + 1;
} else {
dp[j] = Math.max(dp[j], dp[j - 1]);
}
prev = current;
}
}
return dp[n];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String seq1 = scanner.next();
String seq2 = scanner.next();
// 最长公共子序列,空间复杂度O(mn)
String lcs = longestCommonSubsequence(seq1, seq2);
if (!lcs.equals("")) {
System.out.println("LCS: " + lcs + ", 长度为: " + lcs.length());
}else {
System.out.println("0");
}
// // 最长公共子序列,空间复杂度2 * O(min(m, n))
//int res = longestCommonSubsequencesPro(seq1, seq2);
//System.out.println(res);
//// 最长公共子序列,空间复杂度O(min(m, n))
//int res = longestCommonSubsequenceLengthUltra(seq1, seq2);
//System.out.println(res);
}
}
理解最优子结构
最优子结构是指一个问题具有递归结构,并且原问题的最优解可以通过一系列子问题的最优解来构建得到。换句话说,如果一个问题的最优解可以通过其子问题的最优解来推导得出,那么这个问题就具有最优子结构。
最优子结构是动态规划算法中的一个关键概念。在使用动态规划解决问题时,我们将问题划分为若干个子问题,并通过递归地解决子问题来获得原问题的最优解。通过最优子结构的特性,我们可以在求解子问题时将其最优解进行存储,以便后续的计算和使用。
通过将问题划分为子问题,并利用最优子结构的特性,动态规划算法能够避免重复计算,提高效率,并且能够在多项式时间内求解复杂的问题。因此,最优子结构是动态规划算法的一个重要性质,对于设计和分析动态规划算法非常关键。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号