算法导论-第4章-分治法

回忆

在2.3.1中，归并排序使用了分治法。在分治法中，当递归地求解一个问题，在每层递归中执行如下三步骤：

• 分解（Divide）：将问题划分为子问题，子问题的形式与原问题一样，只是规模更小。
• 解决（Conquer）：递归地求解出子问题。如果子问题的规模足够小，则停止递归，直接求解。
• 合并（Combine）：将子问题的解组合成原问题的解。

递归情况（recursive case）：子问题足够大，需要递归求解。

基本情况（base case）：子问题足够小，可以直接求解，不再需要递归。

前言

本章中介绍三个算法和三种求解递归式的方法。

• 第一个算法求解最大子数组问题，其输入是一个数值数组，算法需要确定具有最大和的连续子数组。第二和第三个算法是求解\(n \times n\)矩阵乘法问题的分治算法，其中一个运行时间为\(\Theta(n^3)\)，另一个算法（Strassen算法）的运行时间为\(\Theta(n^{2.81})\)。
• 三种求解递归式的方法，即得出算法“\(\Theta\)”或“\(\Omicron\)”的方法：
  • 代入法：猜测一个界，然后用数学归纳法证明这个界是正确的。
  • 递归树法：将递归式转换为递归树，其结点表示不同层次的递归调用产生的代价，然后用边界和(bounding summations)技术（附录A.2）求解递归式。
  • 主方法：可求解形如\(T(n)=aT(n/b)+f(n),a\ge1,b\gt1\)，生成\(a\)个问题，每个问题的规模是原问题的\(\frac{1}{b}\)，分解和合并步骤代价为\(f(n)\)。

4.1 最大子数组问题

问题引入：假如你投资了某挥发性化学公司，其股价和它生产的化学制品一样都是不稳定的🤣。你被准许在某一时刻买进股票，并在之后某个日期卖出，要求买进卖出都是当天交易结束后进行，作为补偿，你可以了解股票将来的价格。你的目标是收益最大化。下图给出了17天内的股价。

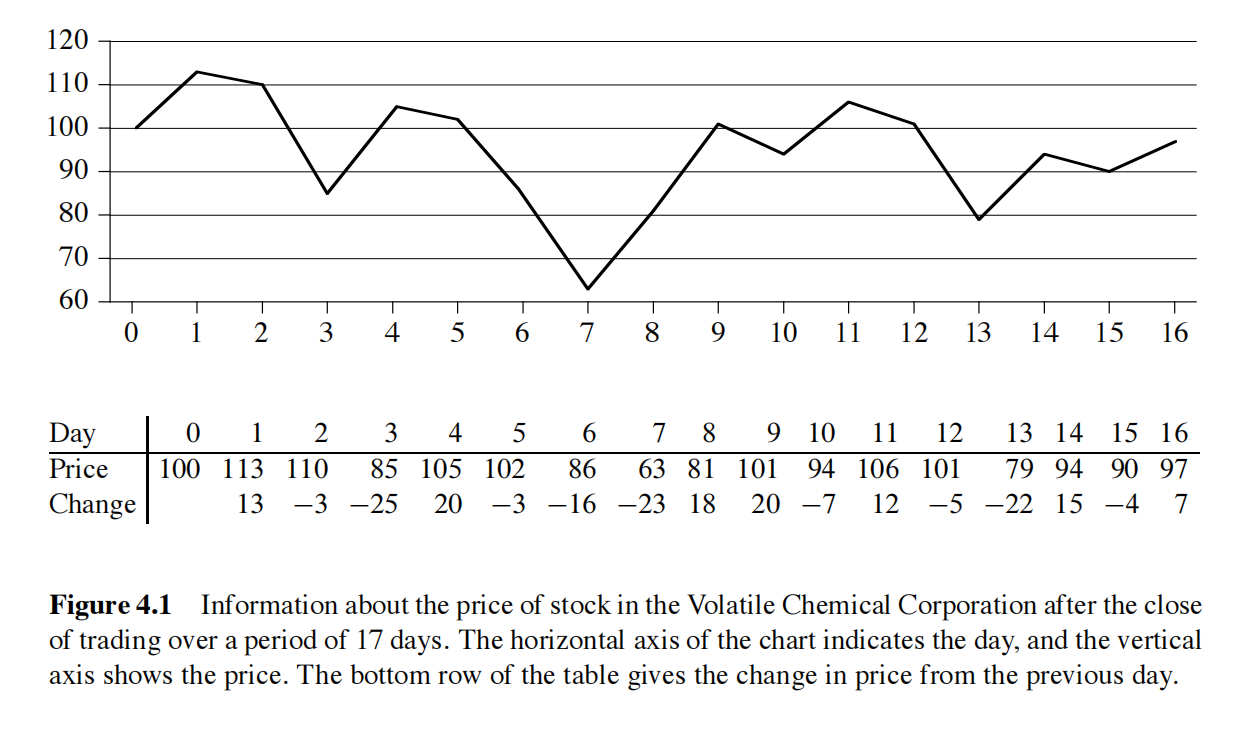
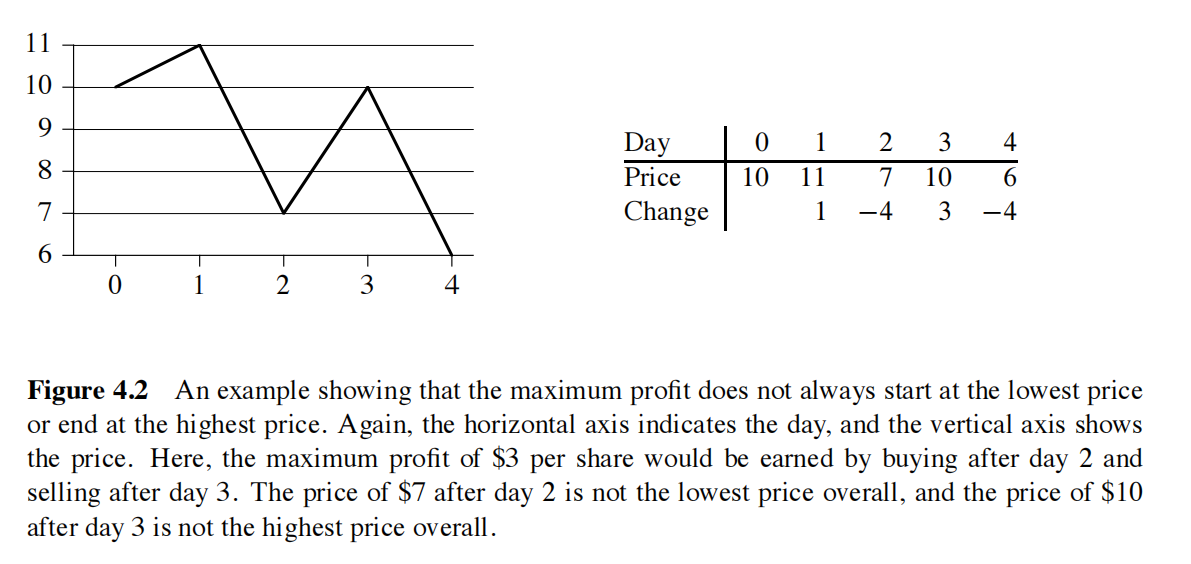
下图证明最大利润有时既不是以最低价格买进，也不是以最高价格卖出。

暴力求解法

计算出\(\begin{pmatrix} n \\ 2 \end{pmatrix}\\\)中日期组合的收益，即所有收益情况。这种方法的运行时间为\(\Omega(n^2)\)。有更好的方法吗？

问题变换

我们的目的是寻找一段时间，使得在这段时间中，从第一天到最后一天的股价净变值最大。因此，我们不再从每日的股价去看待数据，而是考察每日的价格变化，第\(i\)天的价格变化定义为第\(i\)天和第\(i-1\)天的价格差，如下图。

显而易见，只有当数组中包含负数时，最大子数组问题才有意义。如果所有元素都是非负的，最大子数组的和即为整个数组的和。

使用分治法求解

使用分治法意味着我们要将子数组划分为两个规模尽量相等的子数组，也就是说找到中间位置\(mid\)，然后考虑求解两个子数组\(A[low, mid]\)和\(A[mid+1, high]\)。如下图所示，\(A[low, high]\)的任何连续子数组\(A[i..j]\)所处的位置必然是以下三种情况之一：

• 完全位于子数组\(A[low, mid]\)中，因此\(low \le i \le j \le mid\)。
• 完全位于子数组\(A[mid+1, high]\)中，因此\(mid+1 \le i \le j \le high\)。
• 跨越了中点，因此\(low \le i \le mid \le j \le high\)。

因此，\(A[low, high]\)的一个最大子数组所处的位置必然是上述三种情况之一。我们可以递归地求解\(A[low, mid]\)和\(A[mid+1, high]\)的最大子数组，剩下的工作就是寻找跨越中点的最大子数组，然后在三种情况中选取和最大者。

我们可以在线性时间内求出跨越中点的最大子数组。此问题并非原问题规模更小的实例，因为加入了限制--------子数组必须跨越中点。任何跨越中点的子数组都由两个子数组\(A[i..mid]\)和\(A[mid+1..j]\)组成，其中\(low \le i \le mid\)且\(mid \lt j \le high\)。因此只需找出\(A[i..mid]\)和\(A[mid+1..j]\)的最大子数组，然后合并即可。

FIND-MAX-CROSSING-SUBARRAY算法的思想是，从中点分别向左右遍历，分别遍历到左右边界，得到最大子数组的左右边界。

初始调用FIND-MAXIMUM-SUBARRAY(A, 1, A.length)即可求出A[1..n]的最大子数组。

/**
 * 封装一个包含最大子数组信息的类，主要包括以下三个属性：
 * 1、最大子数组的左边界
 * 2、最大子数组的右边界
 * 3、最大子数组中的元素和
 */
class SubarrayResult {
    private int maxLeft; // 左边界
    private int maxRight; // 右边界
    private int sum; // 元素和

    public SubarrayResult() { // 无参构造器
    }

    public SubarrayResult(int maxLeft, int maxRight, int sum) { // 有参构造器
        this.maxLeft = maxLeft;
        this.maxRight = maxRight;
        this.sum = sum;
    }

    /**
     * getter和setter方法
     */
    public int getMaxLeft() {
        return maxLeft;
    }

    public void setMaxLeft(int maxLeft) {
        this.maxLeft = maxLeft;
    }

    public int getMaxRight() {
        return maxRight;
    }

    public void setMaxRight(int maxRight) {
        this.maxRight = maxRight;
    }

    public int getSum() {
        return sum;
    }

    public void setSum(int sum) {
        this.sum = sum;
    }

    @Override
    public String toString() {
        return "SubarrayResult(下标从1开始){" +
                "maxLeft=" + maxLeft +
                ", maxRight=" + maxRight +
                ", sum=" + sum +
                '}';
    }
}

public class FindMaximumSubarray {

    /**
     * 寻找跨越中点的最大子数组
     * @param A
     * @param low
     * @param mid
     * @param high
     * @return SubarrayResult
     */
    public static SubarrayResult findMaxCrossingSubarray(int[] A, int low, int mid, int high) {
        SubarrayResult subarrayResult = new SubarrayResult();

        int leftSum = Integer.MIN_VALUE; // 记录中点左侧的最大子数组和
        int sum = 0; // 记录在遍历过程中的元素和
        for (int i = mid; i >= low; i--) {
            sum += A[i - 1];
            if (sum > leftSum) {
                leftSum = sum;
                subarrayResult.setMaxLeft(i); // 设置跨越中点的最大子数字的左边界（随着遍历不断向左移动）
            }
        }

        int rightSum = Integer.MIN_VALUE; // 记录中点右侧的最大子数组和
        sum = 0;
        for (int j = mid + 1; j <= high; j++) {
            sum += A[j - 1];
            if (sum > rightSum) {
                rightSum = sum;
                subarrayResult.setMaxRight(j); // 设置跨越中点的最大子数字的右边界（随着遍历不断向右移动）
            }
        }
        subarrayResult.setSum(leftSum + rightSum);
        return subarrayResult;
    }

    /**
     * 寻找最大子数组
     * @param A
     * @param low
     * @param high
     * @return
     */
    public static SubarrayResult findMaximumSubarray(int[] A, int low, int high) {
        if (high == low) { // 数组中只有一个元素
            return new SubarrayResult(low, high, A[low - 1]);
        } else {
            int mid = (low + high) / 2; // 以中点划分为左子数组和右子数组
            SubarrayResult subarrayResultLeft = findMaximumSubarray(A, low, mid);
            SubarrayResult subarrayResultRight = findMaximumSubarray(A, mid + 1, high);
            SubarrayResult subarrayResultCrossing = findMaxCrossingSubarray(A, low, mid, high);
            // 检测最大子数组是在“左子数组”还是在“右子数组”还是跨越了中点
            if (subarrayResultLeft.getSum() >= subarrayResultRight.getSum() && subarrayResultLeft.getSum() >= subarrayResultCrossing.getSum()) {
                return subarrayResultLeft;
            } else if (subarrayResultRight.getSum() >= subarrayResultLeft.getSum() && subarrayResultRight.getSum() >= subarrayResultCrossing.getSum()) {
                return subarrayResultRight;
            } else {
                return subarrayResultCrossing;
            }
        }
    }

    public static void main(String[] args) {
        int[] A = {13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7};
        //int A[] = {-500, 10, 5, 5, 2, -3, -29, -10, -50, 22, -23, 10, 150, 1, 9, -900, -26, 3, 99, 7};
        SubarrayResult maximumSubarray = findMaximumSubarray(A, 1, A.length);
        System.out.println(maximumSubarray);
    }
}

// 输出：SubarrayResult(下标从1开始){maxLeft=8, maxRight=11, sum=43}

相似问题：53. 最大子数组和 - 力扣（LeetCode）

4.2 矩阵乘法的Strassen算法

设\(n \times n\)阶矩阵，\(A\)和\(B\)，计算\(C=A \times B\)，

\[c_{ij}=\sum_{k=1}^na_{ik}b_{kj} \]

需要计算\(n^2\)个元素，每个元素是\(n\)个值的和，这\(n\)个值都是通过乘法得到，故要做\(n^3\)次乘法运算。

普通矩阵算法

Strassen矩阵乘法

施特拉森算法在1969年由沃尔克·施特拉森所提出，是第一个时间复杂度低于\(\Omicron(n^3)\)的矩阵乘法算法。由于算法简单理解，且为第一个被提出来的特性，常被算法教材拿来当作主定理（英语：Master theorem)计算时间复杂度的例子。

计算\(C=A \cdot B\)，假设三个矩阵均为\(n \times n\)矩阵，其中\(n\)为2的幂次，这样可以保证子矩阵规模\(n/2\)为整数。

Strassen提出的算法如下：

1. 第一步：将\(n \times n\)的矩阵分解成 4 个\(n/2 \times n/2\)的子矩阵：

   \[A=\begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix},B=\begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix},C=\begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix} \]
   \[\begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix}=\begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \cdot\begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix} \]
   \[C_{11}=A_{11} \cdot B_{11}+A_{12}\cdot B_{21} \]
   \[C_{12}=A_{11} \cdot B_{12}+A_{12}\cdot B_{22} \]
   \[C_{21}=A_{21} \cdot B_{11}+A_{22}\cdot B_{21} \]
   \[C_{22}=A_{21} \cdot B_{12}+A_{22}\cdot B_{22} \]

   按照下标计算方法，此步骤花费\(\Theta(1)\)。

2. 创建10个\(n/2 \times n/2\)的矩阵\(S_1,S_2, \cdots S_{10}\)，每个矩阵保存步骤一中创建的两个子矩阵的和或差。花费时间为\(\Theta(n^2)\)。

   \[S_1=B_{12}-B_{22} \\ S_2=A_{11}+A_{12} \\ S_3=A_{21}+A_{22} \\ S_4=B_{21}-B_{11} \\ S_5=A_{11}+A_{22} \\ S_6=B_{11}+B_{22} \\ S_7=A_{12}-A_{22} \\ S_8=B_{21}+B_{22} \\ S_9=A_{11}-A_{21} \\ S_10=B_{11}+B_{12} \\ \]

3. 根据步骤一中创建的子矩阵和步骤二中创建的10个矩阵，递归地计算7个矩阵积\(P_1,P_2, \cdots P_7\)。每个矩阵\(p_i\)都是\(n/2 \times n/2\)的。

   \[P_1=A_{11} \cdot S_1=A_{11} \cdot B_{12}-A_{11} \cdot B_{22} \\ P_2=S_2 \cdot B_{22}=A_{11} \cdot B_{22}+A_{12} \cdot B_{22} \\ P_3=S_3 \cdot B_{11}=A_{21} \cdot B_{11}+A_{22} \cdot B_{11} \\ P_4=A_{22} \cdot S_4=A_{22} \cdot A_{21}-A_{22} \cdot B_{11} \\ P_5=S_5 \cdot S_6=A_{11} \cdot B_{11}+A_{11} \cdot B_{22}+A_{22} \cdot B_{11}+A_{22} \cdot B_{22} \\ P_6=S_7 \cdot S_8=A_{12} \cdot B_{21}+A_{12} \cdot B_{22}-A_{22} \cdot B_{21}-A_{22} \cdot B_{22} \\ P_7=S_9 \cdot S_{10}=A_{11} \cdot B_{11}+A_{11} \cdot B_{12}-A_{21} \cdot B_{11}-A_{21} \cdot B_{12} \]

4. 通过\(P_i\)矩阵的不同组合进行加减运算，计算出 \(C_{11}, C_{12}, C_{21}, C_{22}\)。花费时间\(\Theta(n^2)\)。

   \[C_{11}=C_{11}+A_{11} \cdot B_{11}+A_{12} \cdot B_{21}=C_{11}+P_5+P_4-P_2+P_6 \\ C_{12}=C_{12}+A_{11} \cdot B_{12}+A_{12} \cdot B_{22}=C_{12}+P_1+P_2 \\ C_{21}=C_{21}+A_{21} \cdot B_{11}+A_{22} \cdot B_{21}=C_{12}+P_3+P_4 \\ C_{22}=C_{22}+A_{21} \cdot B_{12}+A_{22} \cdot B_{22}=C_{22}+P_5+P_1-P_3-P_7 \]

Strassen算法用了 7 次矩阵乘法（计算\(P_i\)） 和18 次矩阵加减法（计算\(S_i\)和\(C_{ij}\)）。

当\(n \gt 1\)时，步骤一、二、四共花费\(\Theta(n^2)\)，步骤三要进行7次\(n/2 \times n/2\)矩阵的乘法运算。因此得到描述Strassen算法运行时间\(T(n)\)的递归式：

\[T(n) =\begin{cases} \Theta(1) & n=1 \\ 7T(n/2)+\Theta(n^2) & n \gt 1 \end{cases} \]

使用递归树或主方法得到解为\(T(n)=\Theta(n^{\log 7})\approx \Theta(n^{2.81})\)。

4.3 代入法求解递归式

代入法求解递归式分两步：

1. 猜测解的形式。（猜测依靠“经验”，偶尔需要创造力）
2. 用数学归纳法求出解中的常熟，并证明解是正确的。

例题：求解\(T(n)=2T(\lfloor n/2 \rfloor)+n\)的上界。

证明：猜测其解\(T(n)=\Omicron(n\log n)\)，代入法要求证明\(\exist \ c \gt 0, \ n_0 \gt 0,\ \forall n \ge n_0, \ 0 \le T(n) \le cn\log n\)，又因为\(T(\lfloor n/2 \rfloor) \le c\lfloor n/2 \rfloor \log(\lfloor n/2 \rfloor)\)，代入到递归式中，得到

\[T(n) \le 2(c\lfloor n/2 \rfloor \log(\lfloor n/2 \rfloor))+n \le cn\log(n/2)+n \\=cn\log n-cn+n \\ \le cn\log n,其中c \ge 1 \]

4.4 递归树法求解递归式

在递归树中，每个结点表示一个单一子问题的代价，子问题对应某次递归函数的调用。我们将树中每层中的代价求和，得到每层代价，然后将所有层的代价求和，得到所有层次递归调用的总代价。

递归式最适合用来生成好的猜测，然后即可用代入法来验证猜测是否正确。

例如，\(T(n)=3T(\lfloor n/4 \rfloor)+\Theta(n^2)\)，

\[T(n)=c n^2+\frac{3}{16} c n^2+\left(\frac{3}{16}\right)^2 c n^2+\cdots+\left(\frac{3}{16}\right)^{\log _4 n} c n^2+\Theta\left(n^{\log _4 3}\right) \\ =\sum_{i=0}^{\log _4 n}\left(\frac{3}{16}\right)^i c n^2+\Theta\left(n^{\log _4 3}\right) \\ <\frac{16}{13} c n^2+\Theta\left(n^{\log _4 3}\right) \\ =O\left(n^2\right) \]

可以用代入法验证下递归树法的结果：

猜测\(T(n) \le dn^2\)，则\(T(n)=3T(n/4)+\Theta(n^2) \le 3d(n/4)^2+cn^2= \frac{3}{16}dn^2+cn^2 \le dn^2，其中n \ge \frac{16}{13}c\)。得证。

4.5 主方法求解递推式

假设有递推式\(T(n)=aT(\frac{n}{b})+f(n)\)，其中\(a \ge 1, b\gt 1\)，\(n\)为问题规模，\(a\)为递归的子问题数量，\(\frac{n}{b}\)为每个子问题的规模（假设每个子问题的规模基本一样），\(f(n)\)为递归以外进行的计算工作。那么\(T(n)\)有如下渐近界：

1. 若存在常数\(\epsilon \gt 0\)，有\(f(n)=\Omicron(n^{\log_ba-\epsilon})\)，则\(T(n)=\Theta(n^{\log_ba})\)。
2. 若\(f(n)=\Omicron(n^{\log_ba})\)，则\(T(n)=\Theta(n^{\log_ba}\log n)\)。
3. 若存在常数\(\epsilon \gt 0\)，有\(f(n)=\Omega(n^{\log_ba+\epsilon})\)，且同时存在常数\(c \lt 1\)以及足够大的\(n\)满足\(af(\frac{n}{b}) \le cf(n)\)，则\(T(n)=\Theta(f(n))\)。

例如，\(T(n)=9T(n/3)+n\)，对于这个递归式，有\(a=9,b=3,f(n)=n\)，因此\(n^{\log_ba}=n^{\log_39}=\Theta(n^2)\)。由于\(f(n)=\Omicron(n^{\log_39-\epsilon})\)，其中\(\epsilon=1\)，满足情况一，从而得到解\(T(n)=\Theta(n^2)\)。

例如，\(T(n)=T(2n/3)+1\)，对于这个递归式，有\(a=1,b=3/2,f(n)=1\)，因此\(n^{\log_ba}=n^{\log_{3/2}1}=n^0=1\)。由于\(f(n)=\Theta(n^{\log_ba})=\Theta(1)\)，满足情况二，从而得到解\(T(n)=\Theta(\log n)\)。

例如，\(T(n)=3T(n/4)+n\log n\)，对于这个递归式，有\(a=3,b=4,f(n)=n\log n\)，因此\(n^{\log_ba}=n^{\log_43}=\Theta(n^{0.793})\)。由于\(f(n)=\Omega(n^{\log_43+\epsilon})\)，其中\(\epsilon\approx0.2\)，当\(n\)足够大时，对于\(c \gt 3/4\)，\(af(n/b)=3(n/4)\log(n/4) \le(3/4)n\log{n}=cf(n)\)。因此满足情况三，从而得到解\(T(n)=\Theta(n\log{n})\)。

参考链接

• 主定理 - 维基百科，自由的百科全书 (wikipedia.org)

• 矩阵乘法Strassen算法 - 知乎 (zhihu.com)