组合数学_第4章_Polya定理
第4章 Polya定理
4.1 群的概念
4.1.1 群的定义
给定一个集合\(G=\{a,b,c,\cdots\}\)和集合\(G\)上的二元运算“\(\cdot\)”,并满足下列4个条件:
-
封闭性:若\(a,b \in G\),则存在\(c \in G\),使得,
\[a \cdot b=c \] -
结合律:对于任意的\(a,b,c \in G\),恒有
\[(a \cdot b) \cdot c = a \cdot (b \cdot c) \] -
存在单位元素:\(G\)中存在一个元素\(e\),使得对于\(G\)的任意元素\(a\),恒有
\[a \cdot e = e \cdot a = a \] -
存在逆元素:对于\(G\)的任意元素\(a\),恒有一个\(b \in G\),使得
\[a \cdot b = b \cdot a = e \]元素\(b\)称为元素\(a\)的逆元素,记作\(a^{-1}\),即
\[b= a^{-1} \]
则称集合\(G\)在运算\(\cdot\)之下是一个群,有时也称\(G\)是一个群,\(G\)中元素\(a\)对\(b\)的运算\(a \cdot b\),可以简记为\(ab\)。
例题:\(G=\{1,-1\}\)在乘法运算下是一个群。
解:(1)封闭性:(1)(-1)=-1,(1)(1)=1,(-1)(1)=-1,(-1)(-1)=1
(2)结合性:显然
(3)单位元素:\(e=1\)
(4)逆元素:由于(1)(1)=1,(-1)(-1)=1,故\((-1)^{-1}=-1,(1)^{-1}=1\)
群的元素个数是有限的,称为有限群。有限群\(G\)的元素个数叫做群的阶,记为\(|G|\)。当群的元素为无限时,称为无限群。
若群\(G\)的任意二元素\(a,b\)恒满足\(ab=ba\)时,称\(G\)为交换群或Abel群。
4.1.2 群的性质
- 群的单位元是唯一的。
- \(ab=ac \Rightarrow b=c,ba=ca \Rightarrow b=c\)
- \(G\)中每一个元素的逆元素是唯一的。
- \((abc \cdots lmn)^{-1}=n^{-1}m^{-1}l^{-1} \cdots c^{-1}b^{-1}a^{-1}\)
- …
设\(G\)是群,\(H\)是\(G\)的子集,若\(H\)在\(G\)的原来定义的运算下也成群,则称\(H\)是\(G\)的子群。
4.2 置换群
置换群是十分重要的群,特别是所有的有限群都可以用它来表示。
不失一般性,假定\(n\)个元素为\(1,2,...,n\)。若元素\(1\)被\(1\)到\(n\)中某一整数\(a_1\)所取代,\(2\)被其中的\(a_2\)元素所取代,…,\(n\)被\(a_n\)所取代,且
用
来表示。
置换群的定义为:设
先做\(p_1\)的置换,再作\(p_2\)的置换:
简单来说就是先经过了\(p_1\)的映射再经过了\(p_2\)的映射。
循环节数:
1置换为3,同时3又能置换为1,这就是一个循环。4置换为4本身,这也算一个循环。左右两个表示是等价的,从后面的表示可以清楚的看到每个循环,以及循环节的个数。
4.3 Polya定理
设\(\overline{G}\)是\(n\)个对象的一个置换群,用\(m\)种颜色涂染这\(n\)个对象,则不同染色的方案数为
其中,\(\overline{G}=\{\overline{a_1},\overline{a_2},\cdots,\overline{a_g}\}\),\(c(\overline{a_k})\)为置换\(\overline{a_k}\)的循环节数。
\(n\)个对象可用\(1,2,...,n\)编号,故\(\overline{G}\)可当作\((1,2,\cdots,n)\)的一个置换群。
例题:用2种颜色去染排成一个环的6个棋子,如果通过旋转得到则只算一种,一共有多少种染色方案?
解:典型的满足polya公式的条件,\(m=2\),\(n=6\)。因为是旋转得到的置换,所以存在6个置换(自己置换到自己也算)。
每个置换的循环节已经标出了。所以根据polya定理公式可以算出,染色方案数为\(\frac{1}{6}(2^1+2^2+2^3+2^2+2^1+2^6)=14\)。
例题:一个3×3的方格,用10种颜色给每个格子染色,旋转0度、90度、180度、270度后相同的算成相同,问总共有多少种方案?

解:
- 旋转0度:(1)(2)(3)(4)(5)(6)(7)(8)(9)
- 旋转90度:(3179)(6248)(5)
- 旋转180度:(19)(28)(37)(46)(5)
- 旋转270度:(7931)(4862)(5)
所以根据Polya定理,总方案数就是\(\frac{1}{4}(10^9+10^3+10^5+10^3)\)。
例题:正六面体的6个面分别用红蓝两种颜色着色,问有多少种方案?
解:使正六面体重合的刚体运动群,有如下几种情况:
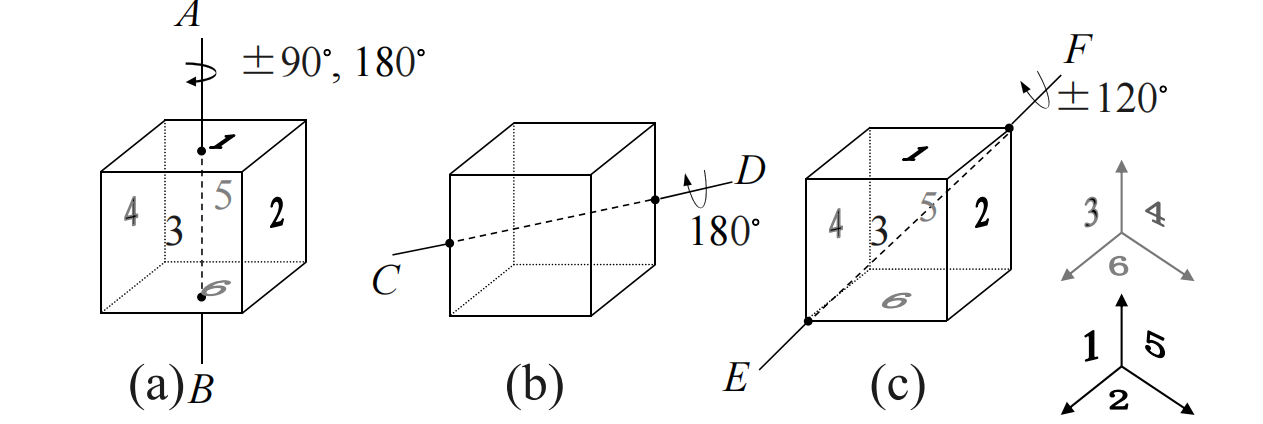
- 不动置换(1)(2)(3)(4)(5)(6),格式为\((1)^6\),只有1种。
- 绕过面1-面6中心的AB轴旋转90度,对应有(1)(2345)(6),旋转-90度,对应有(1)(5432)(6),格式为\((1)^2(4)^1\),正六面体有3个对面,故同类的置换有6个。
- 绕AB轴旋转180度,对应有(1)(24)(35)(6),格式为\((1)^2(2)^2\),同类置换有3个。
- 绕CD轴(棱中-棱中)旋转180度的置换为(16)(25)(34),格式为\((2)^3\),正六面体中对角线位置的平行的棱有6对,故同类的置换有6个。
- 绕正六面体的对角线EF(顶点-顶点)旋转120度,对应有(346)(152),旋转-120度,对应有(643)(251),格式为\((3)^2\),正六面体的对角线有4条,故同类的置换有8个。
根据polya定理,不同的颜色方案为
一种简单的推广:用\(m\)种颜色对正六面体的6个面着色可得不同的方案数\(M\),根据polya定理,
例题:用2种颜色给正6面体的8个顶点着色,有多少种方案?
解:
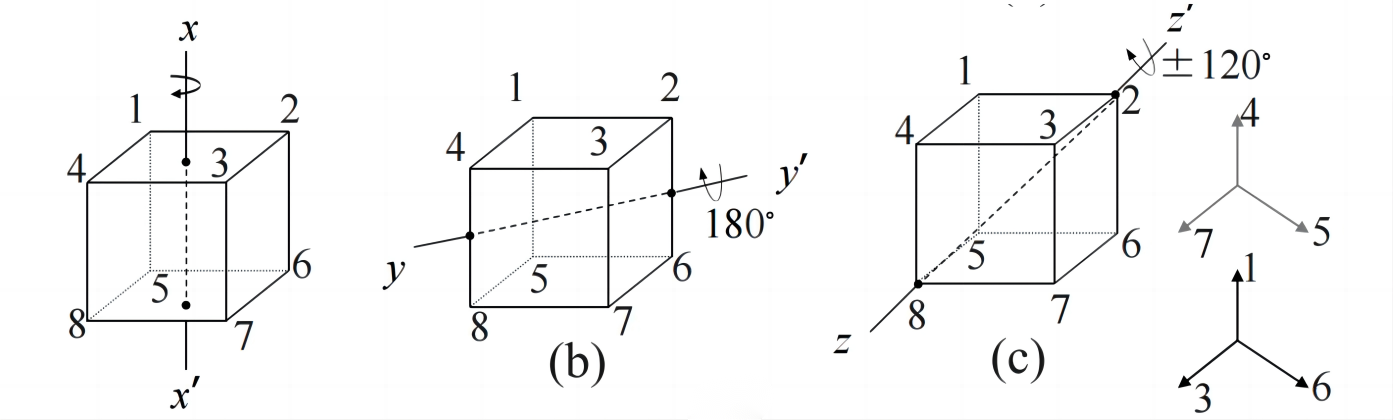
- 不动置换(1)(2)(3)(4)(5)(6)(7)(8),格式为\((1)^8\),只有1种。
- 绕x轴,旋转90度的置换为(1234)(5678),旋转-90度的置换为(4321)(8765),格式为\((4)^2\),正六面体对面有3对,故同类置换有6个。
- 绕x轴,旋转180度的置换为(13)(24)(57)(68),格式为\((2)^4\),正六面体对面有3对,故同类置换有3个。
- 绕y轴,旋转180度的置换为(17)(35)(28)(46),格式为\((2)^4\),正六面体有12条棱,6对棱,故同类置换有6个。
- 绕z轴,旋转120度的置换为(136)(2)(457)(8),旋转-120度的置换为(631)(754),格式为\((3)^2\),正六面体有4条对角线,故同类置换为8个。
根据polya定理,不同的着色方案为,
例题:一个正6面体的6个面用g,r, b, y四种颜色涂染,求其中两个面用色g,两个面用色y, 其余一面用b, 一面用r的方案数。
解:再次看这个图
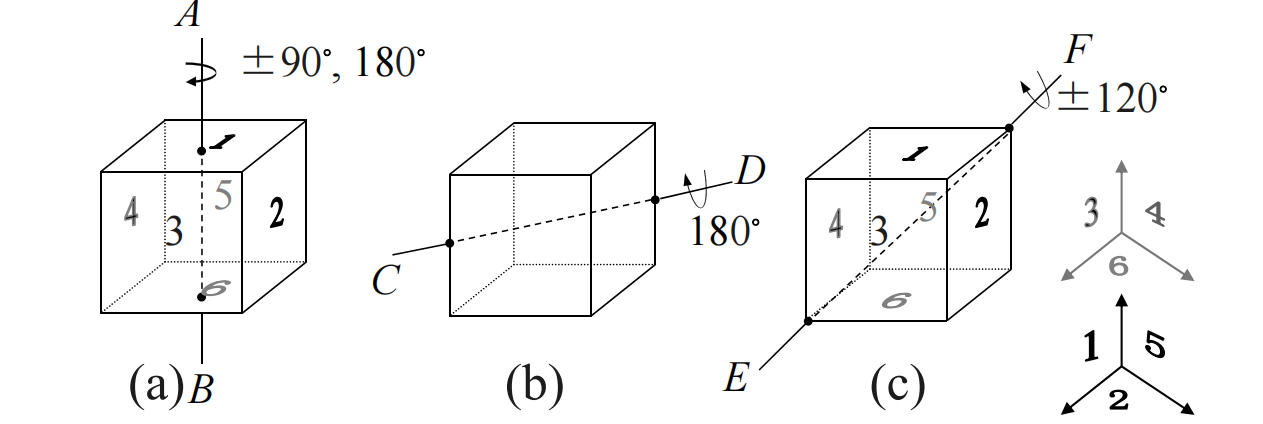
| 分类讨论 | 旋转方式 | 置换群 | 格式 | 同类置换个数 |
|---|---|---|---|---|
| 1 | 不动置换 | (1)(2)(3)(4)(5)(6) | \((1)^6\) | 1 |
| 2 | 绕AB旋转90度和-90度 | (1)(2345)(6)和(1)(5432)(6) | \((1)^2(4)\) | 2×3=6 |
| 3 | 绕AB旋转180度 | (1)(24)(35)(6) | \((1)^2(2)^2\) | 3 |
| 4 | 绕CD旋转180度 | (16)(34)(25) | \((2)^3\) | 6 |
| 5 | 绕EF旋转120度和-120度 | (125)(346)和(521)(643) | \((3)^2\) | 2×4=8 |
由母函数形式的polya定理可得
所求方案数即\(g^2rby^2\)的系数,故方案数为
例题:一个正八面体,用红蓝两色对6个顶点进行着色;用黄绿两种颜色对八个面进行染色,试求其中4个顶点为红色,两个顶点为蓝色,黄和绿的面各四面的方案数。
解:
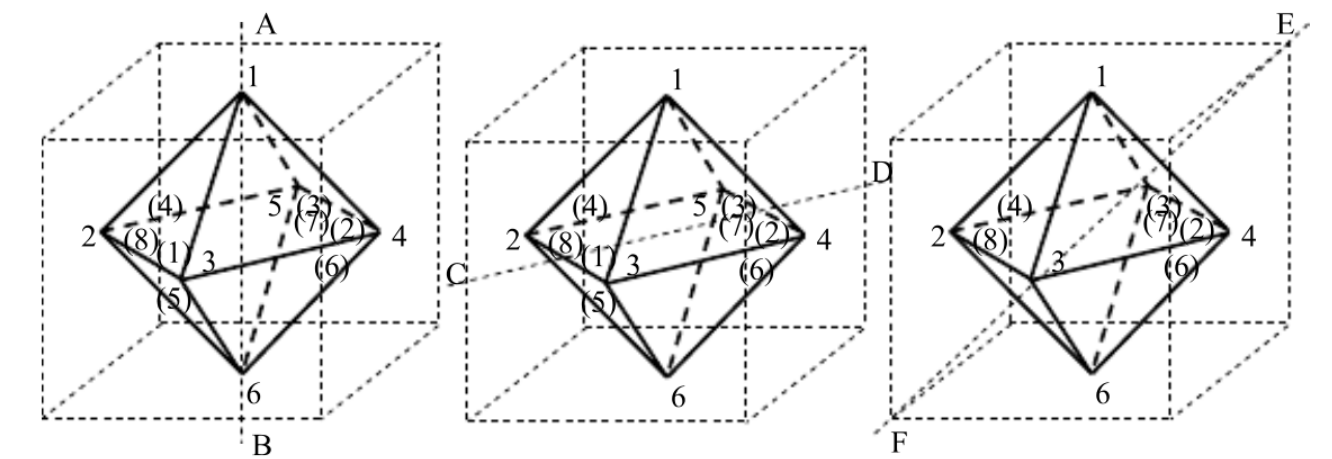
| 分类讨论 | 旋转方式 | 格式 | 同类置换个数 |
|---|---|---|---|
| 1 | 不动置换 | \((1)^6\)-\((1)^8\) | 1 |
| 2 | 绕AB旋转90度和-90度 | \((1)^2(4)\)-\((4)^2\) | 2×3=6 |
| 3 | 绕AB旋转180度 | \((1)^2(2)^2\)-\((2)^4\) | 3 |
| 4 | 绕CD旋转180度 | \((2)^3\)-\((2)^4\) | 6 |
| 5 | 绕EF旋转120度和-120度 | \((3)^2\)-\((1)^2(3)^2\) | 2×4=8 |
根据母函数形式的polya定理,染色方案枚举:
其中\(r^4b^2y^4g^4\)的系数即为所求方案数:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号