组合数学_第2章_递推关系与母函数

第2章 递推关系与母函数

2.1 递推关系

递推关系的引入：

1. 汉诺塔 - 维基百科，自由的百科全书 (wikipedia.org)
2. 斐波那契数 - 维基百科，自由的百科全书 (wikipedia.org)

2.2 母函数

定义：对于序列\(\{a_n\}=a_0,a_1,a_2,...\)，构造一函数\(G(x)=a_0+a_1x+a_2x^2+...\)，称函数\(G(x)\)是序列\(a_0,a_1,a_2,...\)的母函数。例如，\((1+x)^n\)是序列\(C_{n}^{0},C_{n}^{1},C_{n}^{2},...,C_{n}^{n}\)的母函数，序列长度可能是有限的也可能是无限的。

若已知序列\(\{a_n\}\)，则根据定义可知对应的母函数\(G(x)\)；反之，如求得\(G(x)\)，则该序列也随之确定。

根据递推关系求母函数的一种形式算法

所谓形式算法说的是假定这些幂级数在作四则运算时，像有限项的代数式一样。

例题：已知递推关系\(h(n)=2h(n-1)+1，h(1)=1\)，求母函数

解：根据定义设，

\[H(x)=h(0)+h(1)x+h(2)x^2+h(3)x^3+... \]

\(h(0)=0\)，观察递推关系式，两边同时乘以\(-2x\)得，

\[-2xH(x)=-2h(0)x-2h(1)x^2-2h(2)x^3-... \]

两式相加得，

\[(1-2x)H(x)=h(1)x+[h(2)-2h(1)]x^2+[h(3)-2h(2)]x^3+... \]

根据递推公式得其中\(h(1)=1,h(2)-2h(1)=1,h(3)-2h(2)=1,...\)，代入得，

\[(1-2x)H(x)=x+x^2+x^3+...=\frac{x}{1-x} \]

综上得，

\[H(x)=\frac{x}{(1-x)(1-2x)} \]

2.3 Fibonacci序列

例题：\(F(n)=F(n-1)+F(n-2),F(1)=F(2)=1\)

解：根据定义设，

\[G(x)=F(0)+F(1)x+F(2)x^2+F(3)x^3+... \]

\(F(0)=F(2)-F(1)=0\)，观察递推关系式，两边分别乘以\(x\)和\(x^2\)得，

\[xG(x)=F(0)x+F(1)x^2+F(2)x^3+F(3)x^4... \]

\[x^2G(x)=F(0)x^2+F(1)x3+F(2)x^4+F(3)x^5... \]

得，

\[G(x)-xG(x)-x^2G(x)=F(0)+F(1)x-F(0)x+[F(2)-F(1)-F(0)]x^2+[F(3)-F(2)-F(1)]x^3+... \]

根据递推关系得其中\(F(2)-F(1)-F(0)=0,F(3)-F(2)-F(1)=0\)，化简后得，

\[(1-x-x^2)G(x)=x \]

即\(G(x)=\frac{x}{1-x-x^2}\)

2.4 若干等式（了解）

\[F(1)+F(2)+...+F(n)=F(n+2)-1 \]

\[F(1)+F(3)+F(5)+...+F(2n-1)=F(2n) \]

\[F(1)^2+F(2)^2+...+F(n)^2=F(n)F(n+1) \]

2.5 母函数的性质（了解）

1. 若\(b_k=\begin{cases} 0& k\lt l\\a_{k-l}& k \ge l \end{cases}\)，则\(B(x)=x^lA(x)\)
2. 若\(b_k=a_{k+l}\)，则\(B(x)=[A(x)-\sum_{k=0}^{l-1} a_kx^k]/x^l\)
3. 若\(b_k=\sum_{i=0}^k a_i\)，则\(B(x)=\frac{A(x)}{1-x}\)
4. …

2.6 线性常系数齐次递推关系

要求：能够可以根据递推关系，写出特征方程；进而根据特征根直接写出\(a_n\)(中间的步骤直接跳过)

1. 根互不相同的情况

   例题：\(a_{n}-a_{n-1}-12a_{n-2}=0,a_{0}=3,a_{1}=26\)

   解：特征方程\(x^2-x-12=0\)，得\(x_1=4,x_2=-3\)，根据母函数与特征多项式得关系可得，

   \[G(x)=\frac{A}{1-4x}+\frac{B}{1+3x}=A[1+4x+(4x)^2+...]+B[1+(-3x)+(3x)^2+(-3x)^3+...]=(A+B)+[A4+B(-3)]x+[A(4)^2+B(-3)^2]x^2+... \]

   根据母函数定义可知，\(a_n=A(4)^n+B(-3)^n\)，代入\(a_0\)和\(a_1\)得，

   \[\begin{cases} A+B=3& \\4A-3B=26 \end{cases} \]

   计算得，\(A=5,B=-2\)，即\(a_n=5\cdot4^n-2\cdot(-3)^n\)

2. 复根情况

   例题：\(a_n-a_{n-1}+a_{n-2}=0,a_1=1,a_2=0\)

   解：可得\(a_0=1\)，特征方程\(x^2-x+1=0\)，根\(\alpha=\frac{1}{2}\pm\frac{\sqrt{-3}}{2}=\frac{1\pm\sqrt{3}i}{2}\)

   根据\(\alpha\)直接可得，\(a_n=A(\frac{1+\sqrt{3}i}{2})^n+B(\frac{1-\sqrt{3}i}{2})^n\)，接着代入\(a_0\)和\(a_1\)得，\(A=\frac{1}{2}(1-\frac{i}{\sqrt{3}}),B=\frac{1}{2}(1+\frac{i}{\sqrt{3}})\)，即

   \[a_n =\frac{1}{2}(1-\frac{i}{\sqrt{3}})(\frac{1+\sqrt{3}i}{2})^n +\frac{1}{2}(1+\frac{i}{\sqrt{3}})(\frac{1-\sqrt{3}i}{2})^n \]

   根据[欧拉公式](欧拉公式 - 维基百科，自由的百科全书 (wikipedia.org))可知\(\frac{1+\sqrt{3}i}{2}=e^{i\frac{\pi}{3}},\frac{1-\sqrt{3}i}{2}=e^{-i\frac{\pi}{3}}\)，

   \[a_n =\frac{1}{2}(1-\frac{i}{\sqrt{3}})e^{i\frac{n\pi}{3}} +\frac{1}{2}(1+\frac{i}{\sqrt{3}})e^{-i\frac{n\pi}{3}} =\frac{1}{2}(1-\frac{i}{\sqrt{3}})(\cos{\frac{n\pi}{3}}+i\sin{\frac{n\pi}{3}}) +\frac{1}{2}(1+\frac{i}{\sqrt{3}})(\cos{\frac{n\pi}{3}}-i\sin{\frac{n\pi}{3}}) \]

   整理后得，

   \[a_n=\cos{\frac{n\pi}{3}}+\frac{1}{\sqrt{3}}\sin{\frac{n\pi}{3}} \]

3. 二重根情况

   例题：\(a_n-4a_{n-1}+4a_{n-2}=0,a_0=1,a_1=4\)

   解：特征方程\(x^2-4x+4=(x-2)^2=0\)，得\(x_1=x_2=2\)，直接写出\(a_n=(An+B)\cdot2^n\)，剩下代入即可。

2.7 线性常系数非齐次递推关系

要求：能够根据递推关系直接写出\(a_n\)

例题：\(a_n-a_{n-1}-6a_{n-2}=5\cdot4^n\)

解：特征方程\(x^2-x-6=0\)，得\(x_1=3,x_2=-2\)，齐次通解\(a_n=A\cdot3^n+B\cdot(-2)^n\)，又因为得到的两个不同的特征根与非齐次项\(5\cdot4^n\)中的4没有重根，因此直接写出\(a_n=A\cdot3^n+B\cdot(-2)^n+C\cdot4^n\)

---

例题：\(a_n-a_{n-1}-6a_{n-2}=3^n\)

解：特征方程\(x^2-x-6=0\)，得\(x_1=3,x_2=-2\)，齐次通解\(a_n=A\cdot3^n+B\cdot(-2)^n\)，又因为得到的两个不同的特征根与非齐次项\(3^n\)有一个重根3。多一个重根，将前面的多项式最高项提高一次，非齐次特解\(a_n^*=(k_1\cdot n+k_2)\cdot3^n\)，代入递推关系得，

\[(k_1\cdot n+k_2)\cdot3^n-[k_1(n-1)+k_2]\cdot3^{n-1}-6[k_1(n-2)+k_2]\cdot3^{n-2}=3^n \]

整理后待定系数法得，\(k_1=\frac{3}{5},k_2\)未知，即非齐次特解\(a_n^*=(\frac{3}{5}\cdot n+k_2)\cdot3^n\)

非齐次通解\(a_n=(\frac{3}{5}\cdot n+A+k_2)\cdot3^n+B\cdot(-2)^n\)，

令新的\(A=A+k_2\)得，\(a_n=(\frac{3}{5}\cdot n+A)\cdot3^n+B\cdot(-2)^n\)，\(A、B\)是待定常数，由初始条件来确定。

---

例题：\(a_n-3a_{n-1}+2a_{n-2}=6n^2,a_0=6,a_1=7\)

解：特征方程\(x^2-3x+2=0\)，得\(x_1=2,x_2=1\)，齐次通解\(a_n=A\cdot2^n+B\cdot1^n\)，又因为得到得两个不同的特征根与非齐次项\(6n^2\)有一个重根1。多一个重根，将前面的多项式最高项提高一次，非齐次特解\(a_n^*=(k_1\cdot n^3+k_2\cdot n^2+k_3\cdot n+k_4)\cdot1^n\)，代入原非齐次递推关系可得，

\[(k_1\cdot n^3+k_2\cdot n^2+k_3\cdot n+k_4)-3[(k_1\cdot (n-1)^3+k_2\cdot (n-1)^2+k_3\cdot (n-1)+k_4)]+2[(k_1\cdot (n-2)^3+k_2\cdot (n-2)^2+k_3\cdot (n-2)+k_4)]=6n^2 \]

整理得，

\[(k_2+9k_1-3k_2-12k_1+2k_2)n^2 +(k_3-9k_1+6k_2-3k_3+24k_1-8k_2+2k_3)n +(k_4+3k_1-3k_2+3k_3-3k_4-16k_1+8k_2-4k_3+2k_4) =6n^2 \]

化简得，

\[(-3k_1)n^2+(15k_1-2k_2)n+(5k_2-k_3-13k_1)=6n^2 \]

解得，\(k_1=-2,k_2=-15,k_3=-49\)，非齐次特解\(a_n^*=(-2\cdot n^3-15\cdot n^2-49\cdot n+k_4)\)

非齐次通解即为\(a_n=A\cdot2^n+B-2\cdot n^3-15\cdot n^2-49\cdot n+k_4\)，令新得\(B=B+k_4\)得，\(a_n=A\cdot2^n-2\cdot n^3-15\cdot n^2-49\cdot n+B\)，系数\(A、B\)是待定常数，由初始条件决定，代入\(a_0=6,a_1=7\)得，

\[\begin{cases} A+B=6& \\2A+B-66=7 \end{cases} \]

解得，\(A=67,B=-61\)。综上得\(a_n=67\cdot2^n-2\cdot n^3-15\cdot n^2-49\cdot n-61\)

---

定理（用来求线性常系数非齐次递推关系的主要依据）：若非齐次递推关系为\(a_n+c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}=r^nb(n)\)，其中\(b(n)\)是\(n\)的\(p\)次多项式，\(r\)是特征方程\(C(x)=x^k+c_1x^{k-1}+..+c_{k-1}x+c_k=0\)的\(m\)重根，则有特解的形式为\(r^n[k_0n^m+k_1n^{m+1}+...+k_pn^{m+p}]\)，其中\(k_0,k_1,...,k_p\)是待定常数，由非齐次递推关系所确定。若\(r\)不是\(C(x)=0\)的根，则令\(m=0\)。

2.8 递推排列

例题：\(n\)个台阶，一次跨一阶或两阶，多少方案？

解：设\(n\)级台阶每次上一或两个台阶，不同的方案数为\(a_n\)。最后一步跨了一阶，那么有\(a_{n-1}\)种方案；最后一步跨了两阶，那么有\(a_{n-2}\)种方案。\(a_n=a_{n-1}+a_{n-2},a_1=1,a_2=2,a_0=a_2-a_1=1\)

---

例题：由A、B、C、D取\(n\)个做可重复的排列，要求AB至少出现一次，有多少种方案？

解：设所求的方案数为\(a_n\)。有两种情况

（1）直到最后两位才出现AB，也就是说前面\(n-2\)位一次AB也没有出现，即\(4^{n-2}-a_{n-2}\)

（2）前面\(n-1\)位已出现AB，有\(4a_{n-1}\)。注意这里不能写成前面\(n-2\)位已出现AB，这样不能覆盖AB在\(n-1\)和\(n-2\)位的情况

故\(a_n=4a_{n-1}+4^{n-2}-a_{n-2}\)，即\(a_n-4a_{n-1}+a_{n-2}=4^{n-2}\)，\(a_1=0,a_2=1,a_3=8\)。

---

例题：10个数字（0~9）和4个四则运算（+、-、*、/）组成的14个元素，由其中的\(n\)个元素的排列构成一算术表达式的个数。

解：设所求个数为\(a_n\)。因为所求的\(n\)个元素的排列是算术表达式，因此从左到右的最后一个元素一定是数字，而第\(n-1\)位是数字或者运算符。若第\(n-1\)位是数字，则前\(n-1\)位也构成算术表达式，因此有\(10a_{n-1}\)个；若第\(n-1\)位是运算符，则前\(n-2\)位必然构成算术表达式，\(10\cdot4\cdot a_{n-2}=40a_{n-2}\)个。故\(a_n=10a_{n-1}+40a_{n-2}\)，\(a_1=10,a_2=120\)，其中\(a_2\)指的是由从0~99的100个数，以及\(\pm0,\pm1,\pm2,...,\pm9\)构成的算术表达式的个数。

\[\begin{aligned} a_n = &\frac{1}{4 \sqrt{65}}\left[(15+\sqrt{65})(5+\sqrt{65})^n-(15-\sqrt{65})(5\sqrt{65})^n\right]\end{aligned} \]

解递推关系过程略…

---

例题：\(n\)条直线将平面分为多少个域？假定无三线共点，且两两相交

解：设满足条件的\(n\)条直线将平面分成\(D_n\)个域，则第\(n\)条直线被其余\(n-1\)条直线分割成\(n\)段，这\(n\)段正好是新增加的\(n\)个域的边界，因此有\(D_n=D_{n-1}+n,D_1=2\)，

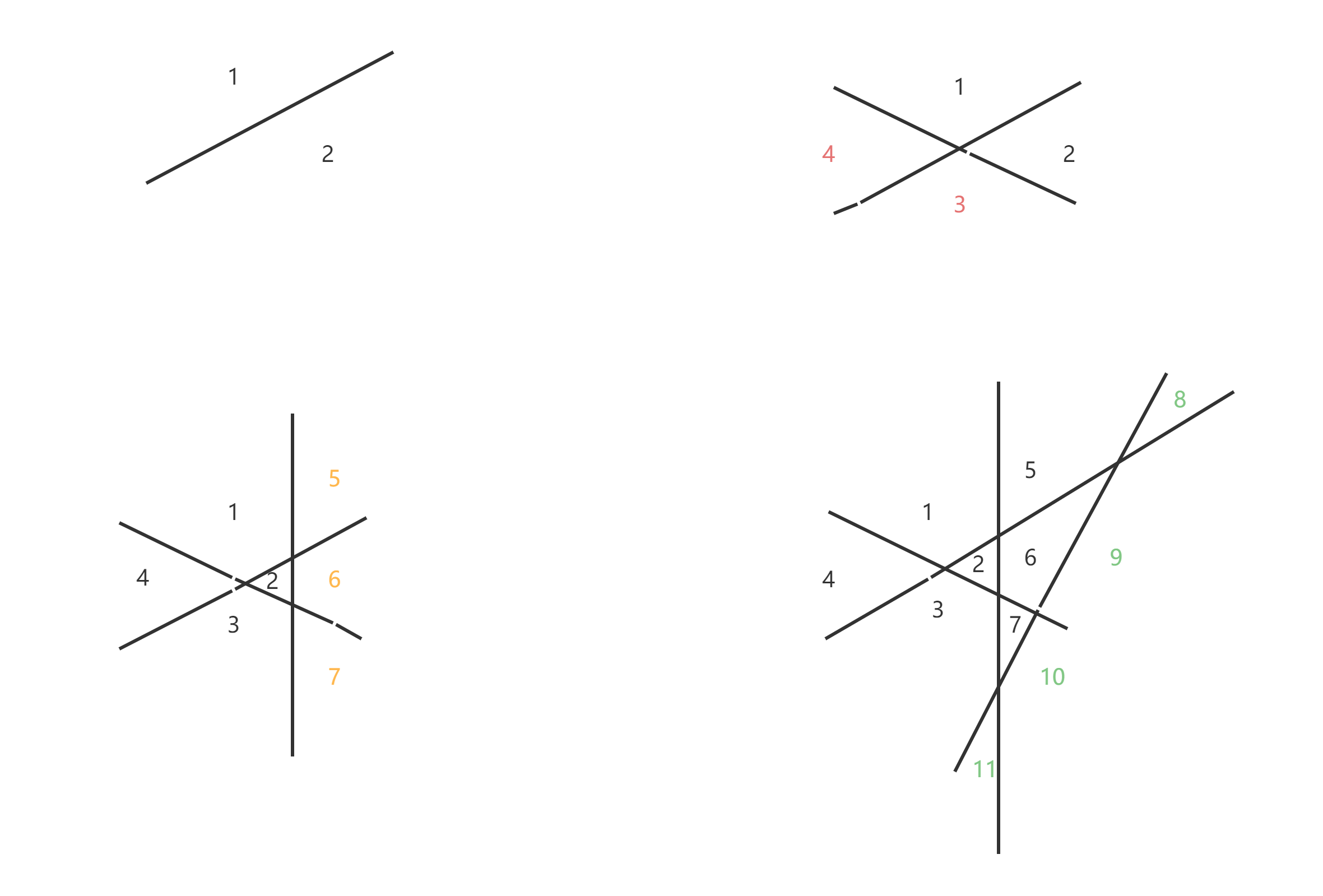
又\(D_1=D_0+1\)，则\(D_0=1\)，利用递推关系可得\(D_n-D_{n-1}=n\)，特征方程\(x-1=0\)，可得\(D_n=(An^2+Bn+C)\cdot1^n\)，又因为\(D_0=1,D_1=2,D_2=4\)，代入得\(A=B=\frac{1}{2}，C=1\)。综上，\(D_n=\frac{1}{2}n(n+1)+1\)。

---

例题：设\(n\)条封闭的曲线，两两相交于两点，任意三条封闭曲线不相交于一点。求这样的\(n\)条曲线把平面分割成几个部分？

解：设满足条件的\(n\)条封闭曲线所分割成的域的数目为\(a_n\)，其中\(n-1\)条封闭曲线所分割成的域的数目为\(a_{n-1}\)。第\(n\)条封闭曲线和这些曲线相交于\(2(n-1)\)个点，这\(2(n-1)\)个点把第\(n\)条封闭曲线截成\(2(n-1)\)条弧，每条弧把\(2(n-1)\)个域中的每个域一分为二。故新增加的域的数为\(2(n-1)\)，则\(a_n=a_{n-1}+2(n-1),a_1=2\)，利用递推关系得\(a_0=2\)。

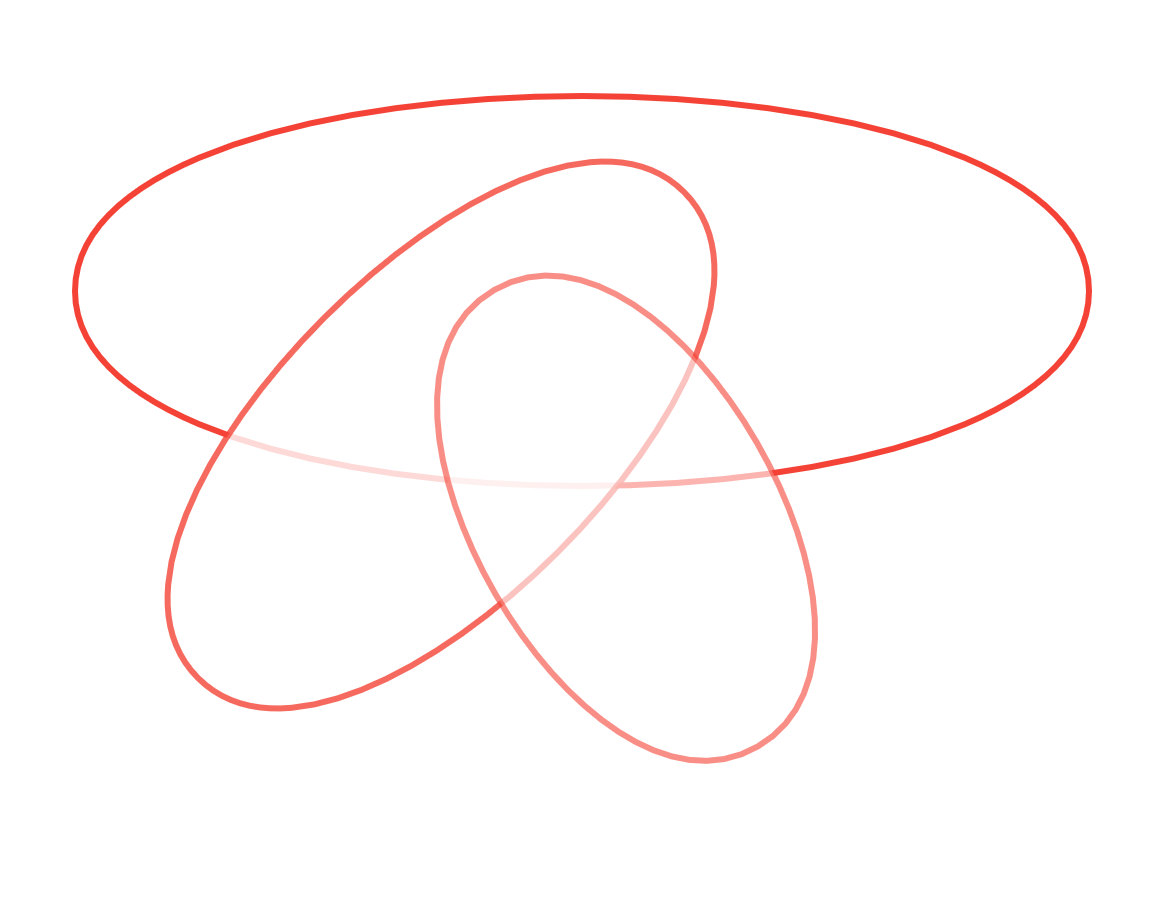
解递推关系过程略…

---

例题：平面上有一点P，它是\(n\)个域\(D_1,D_2,...,D_n\)的共同交界点，如下图。用\(k\)种颜色对这\(n\)个域进行涂色，要求相邻的部分不同色，试问有多少种涂色方案？

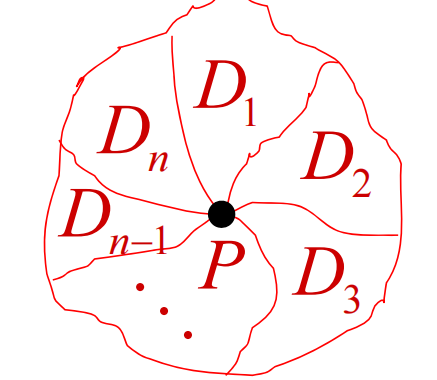
解：令\(a_n\)表示这\(n\)个域的着色方案数。有两种情况：（1）\(D_1\)和\(D_{n-1}\)同色。那么\(D_n\)有\(k-1\)种颜色可用，而且从\(D_1\)到\(D_{n-2}\)的着色方案和\(n-2\)个域的着色方案一一对应。（拿掉\(D_n\)和\(D_{n-1}\)）（2）\(D_1\)和\(D_{n-1}\)不同色。那么\(D_n\)有\(k-2\)种颜色可用，而且从\(D_1\)到\(D_{n-1}\)的着色方案和\(n-1\)个域的着色方案一一对应（拿掉\(D_n\)）。综上，\(a_n=(k-2)a_{n-1}+(k-1)a_{n-2}\)。解递推关系过程略…

---

例题：求下列\(n \times n\)阶行列式的值，

\[d_n=\begin{vmatrix} 1 & 1 & 0 & 0 & ... & 0 & 0 \\ 1 & 1 & 1 & 0 & ... & 0 & 0 \\ 0 & 1 & 1 & 1 & ... & 0 & 0 \\ . & . & . & . & \\ . & . & . & . & \\ . & . & . & . & \\ 0 & 0 & 0 & 0 & ... & 1 & 1 \\ \end{vmatrix} \]

解：行列式按照第一行展开，\(d_n=d_{n-1}-d_{n-2},d_1=1,d_2=0\)，根据递推关系得\(d_0=d_1-d_2=1\)，特征方程为\(x^2-x+1=0\)，\(x=\frac{1\pm\sqrt{3}i}{2}=e^{\pm{\frac{\pi}{3}i}}\)，设\(d_n=k_1\cos{\frac{n\pi}{3}}+k_2\sin{\frac{n\pi}{3}}\)，根据初始条件\(d_0=1,d_1=1\)代入得，\(k_1=1,k_2=\frac{1}{\sqrt{3}}\)，因此\(d_n=\cos{\frac{n\pi}{3}}+\frac{1}{\sqrt{3}}\sin{\frac{n\pi}{3}},n\ge1\)

---

例题：求\(n\)位二进制数最后三位出现010图像得数得个数。

解：对于\(n\)位二进制数\(b_1b_2...b_n\)从左向右扫描，一旦出现010图像，便从这图像后面一位从头开始扫描，例如对11位二进制数00101001010从左到右扫描得结果应该是2-4、7-9位出现010图像，即\(0\overline{010}10\overline{010}10\)，而不是4-6、9-11位出现的010图像，即不是\(001\overline{010}01\overline{010}\)。为了区别于前者起见，我们说后者是“010”，但不是“010图像”。

由于\(n\)位中除了最后三位是010已确定，其余\(n-3\)位可取0或1，故最后3位是010的二进制数的个数是\(2^{n-3}\)。其中包含两种情况：（1）最后3位出现010图像。（2）在\(n-4\)到\(n-2\)位出现010图像。故有

\[a_n+a_{n-2}=2^{n-3},n\ge5 \]

其中\(a_3=1,a_4=2\)（\(a_4=2\)是因为这里的\(n\)是大于等于5的，因此倒数第四位可以是0或1），利用递推得\(a_2=0,a_1=0,a_0=\frac{1}{2}\)，这个题目要求\(n\)位的二进制数，还要去掉首位为0的情况。即\(a_n-a_{n-1}\)。又因为\(a_{n-1}+a_{n-3}=2^{n-4}\)，相减得，

\[a_{n}-2a_{n-1}+a_{n-2}-2a_{n-3}=0 \]

特征方程为\(x^3-2x^2+x-2=0\)，即\((x-2)(x^2+1)=0\)，得\(x_1=2,x_{2,3}=e^{\pm\frac{\pi}{2}i}\)。

根据特征根设，

\[a_n=A \cos \left(n \cdot \frac{\pi}{2}\right)+B \sin \left(n \cdot \frac{\pi}{2}\right)+C \cdot 2^n \]

最后解得，

\[a_n=\frac{2}{5} \cos \left(n \cdot \frac{\pi}{2}\right)-\frac{1}{5} \sin \left(n \cdot \frac{\pi}{2}\right)+\frac{1}{10} \cdot 2^n, n \geq 3 \]

2.9 整数的拆分

定义：整数拆分是指把正整数\(n\)分解成若干正整数的和，不考虑其求和的顺序，一般记为\(n=n_1+n_2+...+n_k,n_1\ge n_2\ge n_3\ge ...\ge n_k\)。例如\(n=2\)，只有一种拆分2=1+1。\(n=3\)，则有1+1+1，2+1两种。\(n=4\)，则有1+1+1+1，2+1+1，2+2，3+1四种。注意与盒子有区别的整数拆分不一样。

正整数\(n\)拆分成若干整数的和，办法不一，不同拆分法的总数叫做拆分数，用\(p(n)\)表示，则\(p(2)=1,p(3)=2,p(4)=4\)。

正整数\(n\)拆分成若干整数的和相当于把\(n\)个无区别的球放到\(n\)个无标志的盒子里，盒子允许空着，也允许放多余一个球。

例题：\((x+y+z)^4\)有多少项？

解：每一项类似于\(x^?y^?z^?,?+?+?=4\)。问题相当于4个无标志的球放到3个有标志的\(x,y,z\)的盒子里，允许空盒的计数。即为\(C(6,4)\)。

---

启发：\(x_1+x_2+...+x_n=m\)放在指数上分解，可以形成不同元素的幂的乘积。

对于上面的例题，我们可以使用不同的幂元来组成这些项，也就是\((1+x+x^2+x^3+x^4)(1+y+y^2+y^3+y^4)(1+z+z^2+z^3+z^4)\)，则该式中一定包含了所有的\(x^?y^?z^?,?+?+?=4\)（包含所有符合的，当然也包含不符合的，不符合的不用管）。

其组合意义是：三个括号分别是不同的幂元表示三个不同的盒子，括号里的幂表示盒子里可能会有几个球，其中1表示盒子里没有球。这里一共四个球，所以最高次幂是4就可以了。

按照这样推广，把每个括号里都扩充到无穷项，就可以覆盖所有的范围，即任意个无区别的球，分到3个有区别的盒子里。

\[(1+x+x^2+x^3+x^4+...)(1+y+y^2+y^3+y^4+...)(1+z+z^2+z^3+z^4+...) \]

若是不关心具体的分球方案（就是每个盒子里到底分了多少个球），只想得到\(n\)个球分到三个不同盒子里有多少种方案，则可以简化为：

\[(1+x+x^2+x^3+x^4+...)^3 \]

继续推广到\(m\)​个不同的盒子

\[(1+x+x^2+x^3+x^4+...)^m \]

则分解后\(x^n\)项前的系数就是\(n\)个球分到\(m\)个不同盒子的方案数。

---

例题：求用1角、2角、3角的邮票贴出不同数值的方案数。

解：因邮票允许重复，故母函数为

\[G(x)=(1+x+x^2+...)(1+x^2+x^4+...)(1+x^3+x^6+...)=\frac{1}{1-x}\cdot\frac{1}{1-x^2}\cdot\frac{1}{1-x^3}=\frac{1}{1-x-x^2+x^4+x^5-x^6} \]

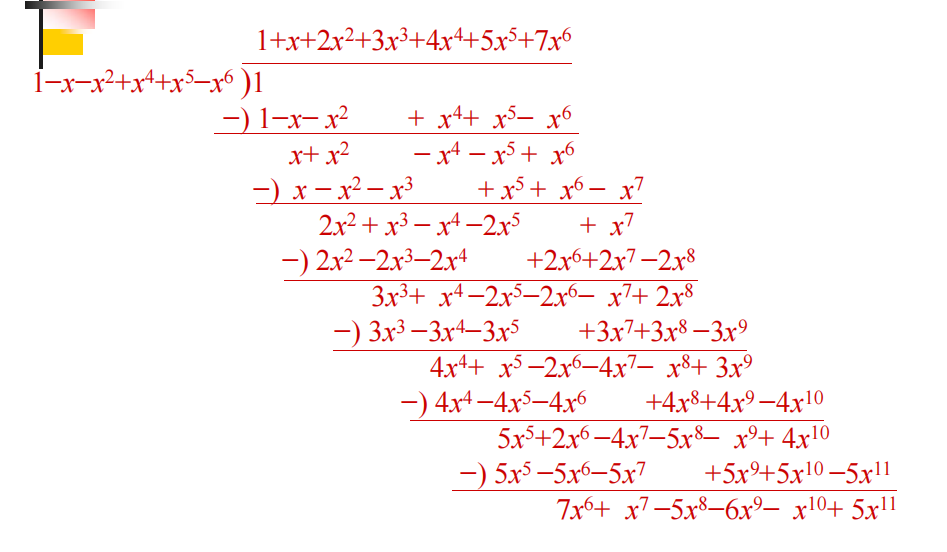
通过长除法得，

\[G(x)=1+x+2x^2+3x^3+4x^4+5x^5+7x^6+... \]

以其中\(7x^6\)项为例，其系数为7，说明贴出6角的方案有7个：111111、11112、1113、1122、123、222、33

---

例题：整数\(n\)拆分成1，2，3，…，m的和，并允许重复，求其母函数。若其中\(m\)至少出现一次，其母函数如何？

解：

\[G_1(x)=(1+x+x^2+\cdots)(1+x^2+x^4+\cdots)......(1+x^m+x^{2m}+\cdots)=\frac{1}{(1-x)(1-x^2)\cdots(1-x^m)} \]

若拆分中\(m\)至少出现一次，其母函数为

\[G_2(x)=(1+x+x^2+\cdots)(1+x^2+x^4+\cdots)......(x^m+x^{2m}+\cdots)=\frac{x^m}{(1-x)(1-x^2)\cdots(1-x^m)} \]

2.10 Ferrers图像

Ferrers图像是研究拆分的一种工具。

定义：一个从上而下的\(n\)层格子，\(m_i\)为第\(i\)层的格子数，当\(m_i\ge m_{i+1},(i=1,2,...,n-1)\)，即上层的格子数不少于下层的格子数时，称之为Ferrers图像。

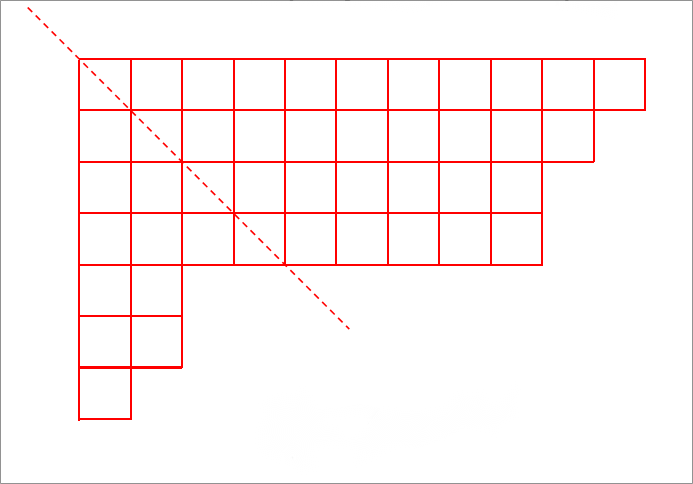
Ferrers图像具有如下性质：

1. 每层至少有一个格子
2. 第一行与第一列互换，第二行与第二列互换，…，即绕虚线轴旋转所得的图仍是Ferrers图像。这两个Ferrers图像称为一对共轭的Ferrers图像。

因整数\(n\)拆分成\(k\)个数的和的拆分可用一\(k\)行的图像表示。所得的Ferrers图像的共轭图像最上面一行有\(k\)个格子。例如：

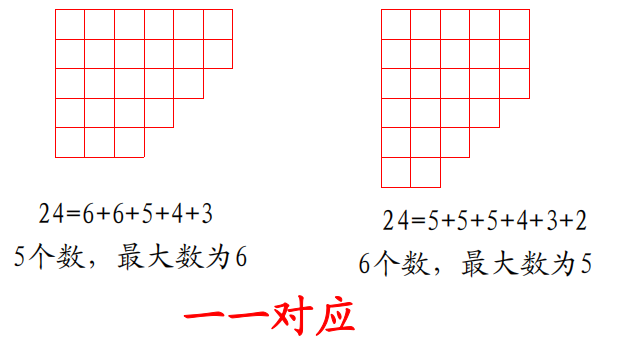
通过Ferrers图像得到关系整数拆分的结论：

1. 整数\(n\)拆分成\(m\)个数的和的拆分数，和将\(n\)拆分成最大数为\(m\)的拆分数相等，反之亦然。
   • 整数\(n\)拆分成\(m\)个数，也就是\(n\)个相同球放到\(m\)个相同的盒子里，不能有空盒。
   • 拆分成最大数为\(m\)，也就是\(n\)的拆分结果里必然有\(m\)且为当前拆分出来的最大数。也就是\(n\)拆成\(1\)到\(m\)的和，允许重复，\(m\)至少一次。即上面例题的第二问。
2. 整数\(n\)拆分成最多不超过\(m\)个数的和的拆分数，和\(n\)拆分成最大数不超过\(m\)的拆分数相等。
   • 整数\(n\)拆分成最多\(m\)个数，也就是\(n\)个相同球放到\(m\)个相同的盒子里，但允许有空盒。
   • 拆分成最大数不超过\(m\)，也就是\(n\)的拆分结果里最大数是\(m\)，但不一定要有。也就是\(n\)拆成\(1\)到\(m\)的和，允许重复，即上面例题的第一问。
3. 整数\(n\)拆分成互不相同的若干奇数的和的拆分数，和\(n\)拆分成有自共轭的Ferrers图像的拆分数相等。

2.11 指数型母函数

定义：对于序列\(a_0,a_1,a_2,...\)，函数\(G_e(x)=a_0+a_1\frac{x}{1!}+a_2\frac{x^2}{2!}+a_3\frac{x^3}{3!}+...+a_k\frac{x^k}{k!}+...\)称为是序列\(a_0,a_1,a_2,...\)的指数型母函数。

指数型母函数是母函数的一种，主要解决允许重复的排列问题。

例题：由a、b、c、d四个字符取5个作允许重复的排列，要求数a出现的次数不超过2次，但不能不出现；b出现次数不超过1次；c出现的次数可达3次，也可以不出现；d出现次数为偶数。求满足上述条件的排列数。

解：

\[G_e(x) = (\frac{x}{1 !}+\frac{x^2}{2 !})(1+x)(1+\frac{x}{1 !}+\frac{x^2}{2 !}+\frac{x^3}{3 !})(1+\frac{x^2}{2 !}+\frac{x^4}{4 !}) \\ =(x+\frac{3}{2} x^2+\frac{1}{2} x^3) (1+x+x^2+\frac{2}{3} x^3+\frac{7}{24} x^4+\frac{1}{8} x^5+\frac{x^6}{48}+\frac{x^7}{144}) \\ =x+\frac{5}{2} x^2+3 x^3+\frac{8}{3} x^4+\frac{43}{24} x^5+\frac{43}{48} x^6+\frac{17}{48} x^7+\frac{1}{288} x^8+\frac{1}{48} x^9+\frac{1}{288} x^{10} \\ =\frac{x}{1 !}+5 \frac{x^2}{2 !}+18 \frac{x^3}{3 !}+64 \frac{x^4}{4 !}+215 \frac{x^5}{5 !}+645 \frac{x^6}{6 !} +1785 \frac{x^7}{7 !}+140 \frac{x^8}{8 !}+7650 \frac{x^9}{9 !}+12600 \frac{x^{10}}{10 !} \]

由此可见，满足条件的排列数共215个。

---

例题：求1，3，5，7，9这5个数字组成的\(n\)位数的个数，要求其中3、7出现的次数为偶数，其他1，5，9出现次数不加限制。

解：设满足条件的\(n\)位的个数为\(a_n\)，则序列\(a_1,a_2,...,a_n,...\)对应的指数型母函数为

\[G_e(x) = (1+\frac{x^2}{2 !}+\frac{x^4}{4 !}+\cdots)^2 (1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\cdots)^3 \]

由于\(e^{-x}=1-x+\frac{x^2}{2 !}-\frac{x^3}{3 !}+\cdots\)，可得

\[\frac{1}{2}(e^x+e^{-x})=1+\frac{x^2}{2 !}+\frac{x^4}{4 !}+\cdots \]

\[G_e(x) =\frac{1}{4}(e^x+e^{-x})^2 e^{3 x} \\ =\frac{1}{4}(e^{2 x}+2+e^{-2 x}) e^{3 x} \\ =\frac{1}{4}(e^{5 x}+2 e^{3 x}+e^x) \\ =\frac{1}{4}(\sum_{n=0}^{\infty} \frac{5^n}{n !} x^n+2 \sum_{n=0}^{\infty} \frac{3^n x^n}{n!}+\sum_{n=0}^{\infty} \frac{x^n}{n !}) \\ =\frac{1}{4} \sum_{n=0}^{\infty}(5^n+2 \cdot 3^n+1) \frac{x^n}{n !} \\ \therefore \quad a_n=\frac{1}{4}(5^n+2 \cdot 3^n+1) \]

2.12 Stirling数

定理：\((x_1+x_2+...+x_n)^m\)展开式的项数等于\(C_{n+m-1}^m\)，而且这些系数之和等于\(n^m\)。

定义：\(n\)个有区别的球放到\(m\)个相同的盒子中，要求没有空盒，其不同的方案数用\(S(n,m)\)b=表示，称为第二类Stirling数。

\(S(n,m)\)也就是将\(n\)个不同的数拆分成\(m\)个非空部分的方案数，也即\(n\)个元素的集合划分成\(m\)个非空子集的方案数。例如，红、黄、蓝、白四种颜色的球，放到两个无区别的盒子里，不允许有空盒，即\(S(4,2)=7\)。

第二类Stirling数\(S(n,k)\)有下列性质：

1. \(S(n,0)=S(0,n)=0,\forall n \epsilon N\)；
2. \(S(n,k)>0,若n \ge k \ge 1\)；
3. \(S(n,k)=0,若k > n \ge 1\)；
4. \(S(n,1)=1,n \ge 1\)；
5. \(S(n,n)=1,n \ge 1\)；
6. \(S(n,2)=2^{n-1}-1\)；
   • 设有\(n\)个不相同的球\(b_1,b_2,b_3,...,b_n\)，从中取出球\(b_1\)，其余的\(n-1\)个球，每个都有与\(b_1\)同盒或不与\(b_1\)同盒两种选择，但必须排除一种选择，即全都与\(b_1\)同盒，这时另一盒将是空盒。故有\(2^{n-1}-1\)种方案。
7. \(S(n,3)=\frac{1}{3!}(3^n-3\times2^n+3)\)；
8. \(S(n, n-1)=(\begin{array}{l}n \\ 2\end{array})\)；
   • \(n\)个球放到\(n-1\)个盒子里，不允许有空盒，故必有一盒有两球，从\(n\)个有区别的球种取2个共有\(C(n,2)\)种方案。
9. \(S(n, n-2)=(\begin{array}{l}n \\ 3\end{array})+3(\begin{array}{l}n \\ 4\end{array})\)；
   • \(n\)个球放到\(n-2\)个盒子里，不允许有空盒，一种情况是一个盒子里有3个球，其他盒子都是一个球，即从\(n\)个有区别的球中取3个有\(C(n,3)\)种方案；另一种情况是有两个盒子里有各有两个球，其他盒子都是一个球，即从\(n\)个有区别的球种取4个，这四个有区别的球可以组成3组，即12和34、13和24、14和23，此时有\(3C(n,4)\)。因此共有\((\begin{array}{l}n \\ 3\end{array})+3(\begin{array}{l}n \\ 4\end{array})\)种方案。

第二类Stirling数满足下面的递推关系：\(S(n,m)=mS(n-1,m)+S(n-1,m-1),n>1,m\ge1\)；

2.13 Catalan数

Catalan数\(h_n\)满足以下递推关系

1. \(h_{n+1}=h_2 h_n+h_3 h_{n-1}+\cdots+h_{n-1} h_3+h_n h_2\),
2. \((n-3) h_n=\frac{n}{2}\left(h_3 h_{n-1}+h_4 h_{n-2}+\cdots\right.\) \(\left.+h_{n-2} h_4+h_{n-1} h_3\right)\).

Catalan数的一般项公式为：

\[C_n=\frac{1}{n+1}(\begin{array} {l} 2n \\ n\end{array})= \frac{(2n)!}{(n+1)!n!} \]

2.14 总结

1. \(n\)个球有区别，\(m\)​个盒子有区别，有空盒。（n个不同元素的集合划分为m个子集，考虑子集的顺序，准许划分出空集）

   \[m^n \]
   \[G_e(x)=(1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\cdots)^m=(e^x)^m \]

2. \(n\)个球有区别，\(m\)个盒子有区别，无空盒。（n个不同元素的集合划分为m个子集，考虑子集的顺序，不准划分出空集）

   \[m!S(n,m) \]
   \[G_e(x)=(x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\cdots)^m=(e^x-1)^m \]

3. \(n\)个球有区别，\(m\)个盒子没区别，有空盒。（n个不同元素的集合划分为m个子集，不考虑子集的顺序，准许划分出空集）

   \[S(n,1)+S(n,2)+\cdots+S(n,m),n\ge m \\ S(n,1)+S(n,2)+\cdots+S(n,n),n\le m \]

4. \(n\)个球有区别，\(m\)个盒子没区别，无空盒。（n个不同元素的集合划分为m个子集，不考虑子集的顺序，不准划分出空集）

   \[S(n,m) \]

5. \(n\)个球无区别，\(m\)​个盒子有区别，有空盒。（正整数n拆分成m个正整数，考虑拆分的顺序，准许拆分出0）(有序的整数拆分)

   \[C(n+m-1,n) \]
   \[G(x)=\frac{1}{(1-x)^m} \]

6. \(n\)个球无区别，\(m\)个盒子有区别，无空盒。（正整数n拆分成m个正整数，考虑拆分的顺序，不准拆分出0）(有序的整数拆分)

   \[C(m+(n-m)-1,n-m)=C(n-1,m-1) \]
   \[G(x)=\frac{x^m}{(1-x)^m} \]

7. \(n\)个球无区别，\(m\)个盒子无区别，有空盒。（正整数n拆分成m个正整数，不考虑拆分的顺序，准许拆分出0）(无序的整数拆分)

   \[G(x)=\frac{1}{(1-x)(1-x^2)\cdots(1-x^m)} \]

8. \(n\)个球无区别，\(m\)个盒子无区别，无空盒。（正整数n拆分成m个正整数，不考虑拆分的顺序，不准拆分出0）(无序的整数拆分)

   \[G(x)=\frac{x^m}{(1-x)(1-x^2)\cdots(1-x^m)} \]

参考公式

1. 二项式定理

\[(a+b)^n=C_{n}^{0}a^{n-0}b^{0}+C_{n}^{1}a^{n-1}b^{1}+C_{n}^{2}a^{n-2}b^{2}+...+C_{n}^{n}a^{n-n}b^{n}，通项T_{k+1}=C_{n}^{k}a^{n-k}b^{k} \]

特别地，当\(a=1,b=x\)时，

\[(1+x)^n=C_{n}^{0}x^{0}+C_{n}^{1}x^{1}+C_{n}^{2}x^{2}+...+C_{n}^{n}x^{n} \]

再特别地，当\(x=1\)时，

\[(1+1)^n=C_{n}+C_{n}^{1}+C_{n}^{2}+...+C_{n}^{n}=2^n \]

2. 常用幂级数展开式

   \[\frac{1}{1-x}=1+x+x^2+x^3+...=\sum_{n=0}^\infty x^n \]
   \[e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...=\sum_{n=0}^\infty \frac{x^n}{n!} \]
   \[\sin{x}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...=\sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!} \]

   其他可通过加减、求导、积分等运算得到！

3. 欧拉公式

   \[e^{ix}=\cos{x}+i\sin{x} \]