哈夫曼树
这一篇要总结的是树中的最后一种,即哈夫曼树,我想从以下几点对其进行总结:
1,什么是哈夫曼树?
2,如何构建哈夫曼树?
3,哈夫曼编码?
4,算法实现?
一,什么是哈夫曼树
什么是哈夫曼树呢?
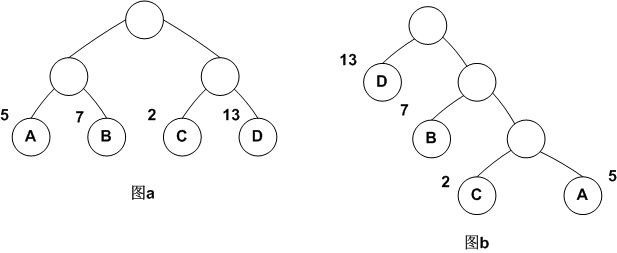
哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。下面用一幅图来说明。
它们的带权路径长度分别为:
图a: WPL=5*2+7*2+2*2+13*2=54
图b: WPL=5*3+2*3+7*2+13*1=48
可见,图b的带权路径长度较小,我们可以证明图b就是哈夫曼树(也称为最优二叉树)。
二,如何构建哈夫曼树
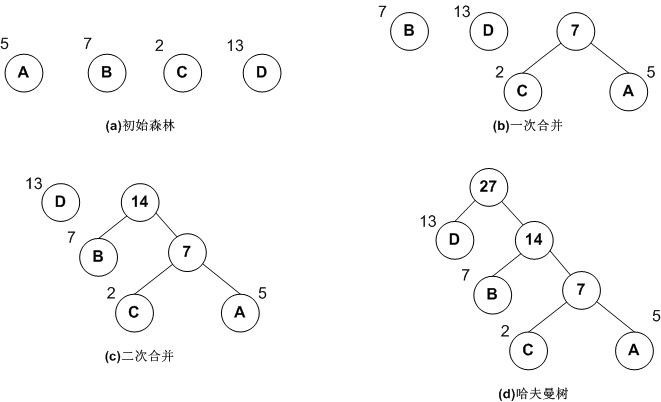
一般可以按下面步骤构建:
1,将所有左,右子树都为空的作为根节点。
2,在森林中选出两棵根节点的权值最小的树作为一棵新树的左,右子树,且置新树的附加根节点的权值为其左,右子树上根节点的权值之和。注意,左子树的权值应小于右子树的权值。
3,从森林中删除这两棵树,同时把新树加入到森林中。
4,重复2,3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
下面是构建哈夫曼树的图解过程:
三,哈夫曼编码
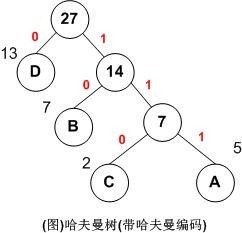
利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径,对路径上的各分支约定指向左子树的分支表示”0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码,即是哈夫曼编码。
就拿上图例子来说:
A,B,C,D对应的哈夫曼编码分别为:111,10,110,0
用图说明如下:
记住,设计电文总长最短的二进制前缀编码,就是以n个字符出现的频率作为权构造一棵哈夫曼树,由哈夫曼树求得的编码就是哈夫曼编码。
四,算法实现
1、节点类
public class Note<T> implements Comparable<Note<T>> { private T data; //数据 private int weight; //权值 private Note<T> left; //左孩子 private Note<T> right; //右孩子 public Note(T data,int weight){ this.data=data; this.weight=weight; } @Override public String toString(){ return "data="+this.data+",weitht="+this.weight; } public T getData() { return data; } public void setData(T data) { this.data = data; } public int getWeight() { return weight; } public void setWeight(int weight) { this.weight = weight; } public Note<T> getLeft() { return left; } public void setLeft(Note<T> left) { this.left = left; } public Note<T> getRight() { return right; } public void setRight(Note<T> right) { this.right = right; } @Override public int compareTo(Note<T> o) { if(o.weight>this.weight){ return 1; }else if(o.weight<this.weight){ return -1; } return 0; } }
2、哈夫曼数操作类
package test1; import java.util.ArrayList; import java.util.Collection; import java.util.Collections; import java.util.LinkedList; import java.util.List; import java.util.Queue; import java.util.Stack; public class HuffmanTree<T> { /** * 创建哈夫曼树 * @param notes * @return */ public static <T> Note<T> createTree(List<Note<T>> notes){ while(notes.size()>1){ Collections.sort(notes); Note<T> left=notes.get(notes.size()-1); Note<T> right=notes.get(notes.size()-2); Note<T> parent=new Note<T>(null,left.getWeight()+right.getWeight()); parent.setLeft(left); parent.setRight(right); notes.remove(left); notes.remove(right); notes.add(parent); } return notes.get(0); } //前序遍历 非递归方式 public static <T> List<Note<T>> breath(Note<T> root){ List<Note<T>> list=new ArrayList<Note<T>>(); Queue<Note<T>> queue=new LinkedList<>(); queue.add(root); while(!queue.isEmpty()){ Note<T> pNode=queue.poll(); list.add(pNode); if(pNode.getLeft()!=null){ queue.add(pNode.getLeft()); } if(pNode.getRight()!=null){ queue.add(pNode.getRight()); } } return list; } /** * 中序遍历 * @param root */ public static <T> void midOrder(Note<T> root) { if (root != null) { midOrder(root.getLeft()); System.out.println(root); midOrder(root.getRight()); } } /** * 前序遍历 * @param root */ public static <T> void preOrder(Note<T> root){ if (root != null) { System.out.println(root); preOrder(root.getLeft()); preOrder(root.getRight()); } } /** * 后序遍历 * @param root */ public static<T> void posOrder(Note<T> root){ if (root != null) { posOrder(root.getLeft()); posOrder(root.getRight()); System.out.println(root); } } /** * 层级遍历 * @param root */ public static<T> void levelOrder(Note<T> root){ if(root==null){ return; } int depth=depth(root); for(int i=1;i<=depth;i++){ levelOrder(root,i); } } private static<T> void levelOrder(Note<T> root,int level){ if(root==null||level<1){ return; } if(level==1){ System.out.println(root); return; } levelOrder(root.getLeft(),level-1); levelOrder(root.getRight(),level-1); } public static<T> int depth(Note<T> root){ if(root==null){ return 0; } int l=depth(root.getLeft()); int r=depth(root.getRight()); return l>r?l+1:r+1; } }
3、测试类
package test1; import java.util.ArrayList; import java.util.List; public class HuffmanTreeTest { public static void main(String[] args ){ List<Note<String>> list=new ArrayList<Note<String>>(); list.add(new Note<String>("b",5)); list.add(new Note<String>("a",7)); list.add(new Note<String>("d",2)); list.add(new Note<String>("c",4)); Note<String> root=HuffmanTree.createTree(list); //System.out.println(HuffmanTree.breath(root)); HuffmanTree.midOrder(root); System.out.println("============================"); HuffmanTree.preOrder(root); System.out.println("============================"); HuffmanTree.posOrder(root); System.out.println("============================"); HuffmanTree.levelOrder(root); } }
4、测试结果