我的模板(持续更新ing)[早就不更新了]
头文件
短的:

1 #include<bits/stdc++.h> 2 #define cl(a,b) memset(a,b,sizeof(a)) 3 #define debug(a) cerr<<#a<<"=="<<a<<endl 4 using namespace std; 5 typedef long long ll; 6 typedef pair<int,int> pii; 7 8 const int maxn=1e5+10; 9 10 int main() 11 { 12 13 return 0; 14 }/* 15 16 17 18 */
长的:

1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cmath> 5 #include<cstring> 6 #include<string> 7 #include<ctime> 8 #include<map> 9 #include<set> 10 #include<vector> 11 #include<queue> 12 #include<cstdlib> 13 #include<cassert> 14 #include<sstream> 15 #include<stack> 16 #include<list> 17 #include<bitset> 18 #define cl(a,b) memset(a,b,sizeof(a)) 19 #define debug(x) cerr<<#x<<"=="<<(x)<<endl 20 using namespace std; 21 typedef long long ll; 22 typedef long double ldb; 23 typedef pair<int,int> pii; 24 25 const int inf=0x3f3f3f3f; 26 const int maxn=1e9+10; 27 const int mod=1e7+7; 28 const double eps=1e-8; 29 const double pi=acos(-1); 30 31 int dx[8]= {0,0,1,-1,1,-1,1,-1}; 32 int dy[8]= {1,-1,0,0,-1,1,1,-1}; 33 34 ll gcd(ll a,ll b){return a?gcd(b%a,a):b;} 35 ll powmod(ll a,ll x,ll mod){ll t=1;while(x){if(x&1)t=t*a%mod;a=a*a%mod;x>>=1;}return t;} 36 //---------------------------------------ヽ(^。^)丿 37 int main() 38 { 39 40 return 0; 41 } 42 /* 43 44 45 46 */
超神读入挂

1 #define JUDGE 2 3 #ifdef DEBUG 4 inline bool read(int &ret) 5 { 6 if(scanf("%d",&ret)==EOF) return false; 7 return true; 8 } 9 #endif DEBUG 10 11 #ifdef JUDGE 12 namespace fastIO { 13 #define BUF_SIZE 100000 14 //fread -> read 15 bool IOerror = 0; 16 inline char nc() { 17 static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE; 18 if(p1 == pend) { 19 p1 = buf; 20 pend = buf + fread(buf, 1, BUF_SIZE, stdin); 21 if(pend == p1) { 22 IOerror = 1; 23 return -1; 24 } 25 } 26 return *p1++; 27 } 28 inline bool blank(char ch) { 29 return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t'; 30 } 31 inline bool read(int &x) { 32 char ch; 33 while(blank(ch = nc())); 34 if(IOerror) 35 return false; 36 for(x = ch - '0'; (ch = nc()) >= '0' && ch <= '9'; x = x * 10 + ch - '0'); 37 return true; 38 } 39 #undef BUF_SIZE 40 }; 41 using namespace fastIO; 42 #endif JUDGE
矩阵快速幂

1 struct matrix 2 { 3 ll a[maxn][maxn]; 4 int row,col; 5 matrix():row(maxn),col(maxn){cl(a,0);} 6 matrix(int x,int y):row(x),col(y){cl(a,0);} 7 void show() 8 { 9 for(int i=0; i<row; i++) 10 { 11 for(int j=0; j<col; j++) 12 { 13 printf("%d%c",a[i][j],j==col-1?'\n':' '); 14 } 15 } 16 } 17 inline ll* operator [] (int x) 18 { 19 return a[x]; 20 } 21 inline matrix operator * (matrix x) 22 { 23 matrix tmp(row,col); 24 for (int i=0; i<row; i++) 25 for (int j=0; j<col; j++) 26 for (int k=0; k<row; k++) 27 tmp[i][j]=(tmp[i][j]+a[i][k]*x[k][j])%mod; 28 return tmp; 29 } 30 inline void operator *= (matrix x) 31 { 32 *this = *this * x; 33 } 34 matrix operator ^ (ll x) 35 { 36 matrix result(row,col),now=*this; 37 for(int i=0; i<row; i++) 38 { 39 result[i][i]=1; 40 } 41 while(x) 42 { 43 if(x%2) result*=now; 44 now*=now; 45 x/=2; 46 } 47 return result; 48 } 49 };
降维线段树(区间更新+单点更新)

1 #define ls getid(l,l+r>>1) 2 #define rs getid((l+r>>1)+1,r) 3 #define lson l,m,ls 4 #define rson m+1,r,rs 5 6 typedef long long ll; 7 8 const int maxn = 1e5+10; 9 10 inline int getid(int x,int y) 11 { 12 return x+y|y!=x; 13 } 14 15 ll rm[maxn<<1],col[maxn<<1]; 16 17 void pushup(int l,int r,int rt) 18 { 19 rm[rt]=rm[ls]+rm[rs]; 20 } 21 22 void pushdown(int l,int r,int rt,int k) 23 { 24 if (col[rt]) 25 { 26 col[ls] += col[rt]; 27 col[rs] += col[rt]; 28 rm[ls] += col[rt]*(k-(k>>1)); 29 rm[rs] += col[rt]*(k>>1); 30 col[rt] = 0; 31 } 32 } 33 34 void build(int l,int r,int rt) 35 { 36 if(l == r) 37 { 38 scanf("%I64d",&rm[rt]); 39 return ; 40 } 41 int m=l+r>>1; 42 build(lson); 43 build(rson); 44 pushup(l,r,rt); 45 } 46 47 void update(int L,int R,int c,int l,int r,int rt) 48 {//区间更新 49 if(L<=l && r<=R) 50 { 51 col[rt]+=c; 52 rm[rt]+=c*(r-l+1); 53 return ; 54 } 55 pushdown(l,r,rt,r-l+1); 56 int m=l+r>>1; 57 if( L <= m ) update(L,R,c,lson); 58 if (R > m) update(L,R,c,rson); 59 pushup(l,r,rt); 60 } 61 62 void update(int p,int c,int l,int r,int rt) 63 {//单点更新 64 if(l==r) 65 { 66 rm[rt]+=c; 67 return ; 68 } 69 int m=l+r>>1; 70 if( p <= m ) update(p,c,lson); 71 else update(p,c,rson); 72 pushup(l,r,rt); 73 } 74 75 ll query(int L,int R,int l,int r,int rt) 76 { 77 if( L<=l && r<=R ) 78 { 79 return rm[rt]; 80 } 81 pushdown(l,r,rt, r-l+1); 82 int m=l+r>>1; 83 ll ret = 0; 84 if( L<=m ) ret += query(L,R,lson); 85 if( m<R ) ret += query(L,R,rson); 86 return ret; 87 } 88 89 int main() 90 { 91 int n,m; 92 scanf("%d%d",&n,&m); 93 char str[2]; 94 build(1,n,1); 95 while(m--) 96 { 97 int l,r,x; 98 scanf("%s",str); 99 if(str[0]=='Q') 100 { 101 scanf("%d%d",&l,&r); 102 printf("%I64d\n",query(l,r,1,n,1)); 103 } 104 else 105 { 106 scanf("%d %d %d", &l, &r, &x); 107 update(l, r, x, 1, n, 1); 108 } 109 } 110 return 0; 111 }
字典树求异或值

1 typedef long long ll; 2 3 const int maxn=1e5+10; 4 5 struct t 6 { 7 ll tree[32*maxn][3];//字典树的树部分 8 ll val[32*maxn];//字典树的终止节点 9 ll cnt;//字典树的大小 10 void init() //初始化字典树 11 { 12 cl(tree,0); 13 cl(val,0); 14 cnt=1; 15 } 16 void add(ll a) 17 { 18 int x=0,now; 19 for(int i=32; i>=0; i--) 20 { 21 now=((a>>i)&1); //当前位数 22 if(tree[x][now]==0) //没有的这个节点的话 加入这个节点 23 { 24 cl(tree[cnt],0); 25 val[cnt]=0; 26 tree[x][now]=cnt++; 27 } 28 x=tree[x][now]; 29 } 30 val[x]=a; //结尾标记 31 } 32 ll Search(ll a) //查找字典树中和a异或起来最大的值 33 { 34 int x=0,now; 35 for(int i=32; i>=0; i--) 36 { 37 now=!((a>>i)&1); 38 if(tree[x][now]) //如果和当前位相反的这个节点存在 39 { 40 x=tree[x][now]; //那么继续找这个节点下的子树 41 } 42 else 43 { 44 x=tree[x][!now]; //不存在就找自己这个节点下的子树 45 } 46 } 47 return val[x]; //结尾标记就是这个数字 48 } 49 } Trie;
马拉车算法求最长回文串

1 string longestPalindrome(string ss) 2 { 3 string s="#"; 4 for(auto i:ss) 5 { 6 s+=i; 7 s+="#"; 8 } 9 int c=0,r=0; 10 vector<int>p(s.size(),0); 11 for(int i=0;i<s.size();i++) 12 { 13 if(r>i) p[i]=min(r-i,p[2*c-i]); 14 while((i-1-p[i])>=0 15 &&(i+1+p[i])<s.size() 16 &&s[i+1+p[i]]==s[i-1-p[i]]) 17 p[i]++; 18 if(i+p[i]>r) 19 { 20 r=i+p[i]; 21 c=i; 22 } 23 } 24 int ans=0,mid=0; 25 for(int i=0;i<s.size();i++) 26 { 27 if(p[i]>ans) 28 { 29 ans=p[i]; 30 mid=i; 31 } 32 } 33 return ss.substr((mid-ans)/2,ans); 34 }
lucas定理

1 ll fac[maxn]; 2 3 ll quick_pow(ll a,ll n) 4 { 5 ll ans=1; 6 while(n) 7 { 8 if(n%2) ans=1ll*ans*a%mod; 9 a=1ll*a*a%mod; 10 n>>=1; 11 } 12 return ans; 13 } 14 15 ll inv(ll a) 16 { 17 return quick_pow(a,mod-2); 18 } 19 20 void init() 21 { 22 fac[0]=1; 23 for(int i=1;i<maxn;i++) 24 { 25 fac[i]=1ll*fac[i-1]*i%mod; 26 } 27 } 28 29 ll C(ll a,ll b) 30 { 31 ll ans=1; 32 if(a<b || b<0) return 0; 33 while(a&&b) 34 { 35 ll aa=a%mod,bb=b%mod; 36 if(aa<bb) return 0;; 37 ans = 1ll*ans*fac[aa]%mod * inv(1ll*fac[bb]*fac[aa-bb]%mod)%mod; 38 a/=mod,b/=mod; 39 } 40 return ans; 41 }
O(n)预处理Cm n

1 const int maxn=1e6+10; 2 const int mod=1e9+7; 3 ll fac[maxn],f[maxn],inv[maxn]; 4 5 void init() 6 { 7 fac[0]=fac[1]=f[0]=f[1]=inv[0]=inv[1]=1; 8 for(int i=2;i<maxn;i++) 9 { 10 fac[i]=fac[i-1]*i%mod; // n! 11 ll t=mod/i,k=mod%i; 12 f[i]=(mod-t)*f[k]%mod; // n的逆元 13 inv[i]=inv[i-1]*f[i]%mod; // n!的逆元 14 } 15 } 16 17 ll C(ll n,ll m) 18 { 19 if(n<m) return 0; 20 return fac[n]*inv[m]%mod*inv[n-m]%mod; 21 }
自适应simpson积分

1 double simpson(double a,double b) 2 { 3 double c=a+(b-a)/2; 4 return (f(a)+4*f(c)+f(b))*(b-a)/6; 5 } 6 7 double asr(double a,double b,double eps,double A) 8 { 9 double c=a+(b-a)/2; 10 double L=simpson(a,c); 11 double R=simpson(c,b); 12 if(fabs(L+R-A)<=15*eps) return L+R+(L+R-A)/15.0; 13 return asr(a,c,eps/2,L)+asr(c,b,eps/2,R); 14 } 15 16 double asr(double a,double b,double eps) 17 { 18 return asr(a,b,eps,simpson(a,b)); 19 }
日期公式

1 int zeller(int y,int m,int d) 2 {//计算星期几 3 if(m<=2) y--,m+=12; 4 int c=y/100;y%=100; 5 int w=((c>>2)-(c<<1)+y+(y>>2)+(13*(m+1)/5)+d-1)%7; 6 if(w<0) w+=7; return (w); 7 } 8 9 int getid(int y,int m,int d) 10 {//计算每个日期的id 可以计算两个日期之间的天数 11 if(m<3) {y--;m+=12;} 12 return 365*y+y/4-y/100+y/400+(153*m+2)/5+d; 13 }
费用流(uva11248)

1 // UVa11248 Frequency Hopping:使用Dinic算法 2 // Rujia Liu 3 #include<cstdio> 4 #include<cstring> 5 #include<queue> 6 #include<vector> 7 #include<algorithm> 8 using namespace std; 9 10 const int maxn = 100 + 10; 11 const int INF = 1000000000; 12 13 struct Edge 14 { 15 int from, to, cap, flow; 16 bool operator < (const Edge& b) 17 { 18 return from < b.from || (from == b.from && to < b.to); 19 } 20 }; 21 22 struct Dinic 23 { 24 int n, m, s, t; //点的编号从0开始 25 vector<Edge> edges; // 边数的两倍 26 vector<int> G[maxn]; // 邻接表,G[i][j]表示结点i的第j条边在e数组中的序号 27 bool vis[maxn]; // BFS使用 28 int d[maxn]; // 从起点到i的距离 29 int cur[maxn]; // 当前弧指针 30 31 void ClearAll(int n) 32 { 33 for(int i = 0; i < n; i++) G[i].clear(); 34 edges.clear(); 35 } 36 37 void ClearFlow() 38 { 39 for(int i = 0; i < edges.size(); i++) edges[i].flow = 0; 40 } 41 42 void AddEdge(int from, int to, int cap) 43 { 44 edges.push_back((Edge){from, to, cap, 0}); 45 edges.push_back((Edge){to, from, 0, 0}); 46 m = edges.size(); 47 G[from].push_back(m-2); 48 G[to].push_back(m-1); 49 } 50 51 bool BFS() 52 { 53 memset(vis, 0, sizeof(vis)); 54 queue<int> Q; 55 Q.push(s); 56 vis[s] = 1; 57 d[s] = 0; 58 while(!Q.empty()) 59 { 60 int x = Q.front(); 61 Q.pop(); 62 for(int i = 0; i < G[x].size(); i++) 63 { 64 Edge& e = edges[G[x][i]]; 65 if(!vis[e.to] && e.cap > e.flow) 66 { 67 vis[e.to] = 1; 68 d[e.to] = d[x] + 1; 69 Q.push(e.to); 70 } 71 } 72 } 73 return vis[t]; 74 } 75 76 int DFS(int x, int a) 77 { 78 if(x == t || a == 0) return a; 79 int flow = 0, f; 80 for(int& i = cur[x]; i < G[x].size(); i++) 81 { 82 Edge& e = edges[G[x][i]]; 83 if(d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap-e.flow))) > 0) 84 { 85 e.flow += f; 86 edges[G[x][i]^1].flow -= f; 87 flow += f; 88 a -= f; 89 if(a == 0) break; 90 } 91 } 92 return flow; 93 } 94 95 int Maxflow(int s, int t) 96 { 97 this->s = s; 98 this->t = t; 99 int flow = 0; 100 while(BFS()) 101 { 102 memset(cur, 0, sizeof(cur)); 103 flow += DFS(s, INF); 104 } 105 return flow; 106 } 107 108 vector<int> Mincut() // call this after maxflow 109 { 110 vector<int> ans; 111 for(int i = 0; i < edges.size(); i++) 112 { 113 Edge& e = edges[i]; 114 if(vis[e.from] && !vis[e.to] && e.cap > 0) ans.push_back(i); 115 } 116 return ans; 117 } 118 119 void Reduce() 120 { 121 for(int i = 0; i < edges.size(); i++) edges[i].cap -= edges[i].flow; 122 } 123 }; 124 125 Dinic g; 126 127 int main() 128 { 129 int n, e, c, kase = 0; 130 while(scanf("%d%d%d", &n, &e, &c) == 3 && n) 131 { 132 g.ClearAll(n); 133 while(e--) 134 { 135 int b1, b2, fp; 136 scanf("%d%d%d", &b1, &b2, &fp); 137 g.AddEdge(b1-1, b2-1, fp); 138 } 139 int flow = g.Maxflow(0, n-1); 140 printf("Case %d: ", ++kase); 141 if(flow >= c) printf("possible\n"); 142 else 143 { 144 vector<int> cut = g.Mincut(); 145 g.Reduce(); 146 vector<Edge> ans; 147 for(int i = 0; i < cut.size(); i++) 148 { 149 Edge& e = g.edges[cut[i]]; 150 e.cap = c; 151 g.ClearFlow(); 152 if(flow + g.Maxflow(0, n-1) >= c) ans.push_back(e); 153 e.cap = 0; 154 } 155 if(ans.empty()) printf("not possible\n"); 156 else 157 { 158 sort(ans.begin(), ans.end()); 159 printf("possible option:(%d,%d)", ans[0].from+1, ans[0].to+1); 160 for(int i = 1; i < ans.size(); i++) 161 printf(",(%d,%d)", ans[i].from+1, ans[i].to+1); 162 printf("\n"); 163 } 164 } 165 } 166 return 0; 167 }
数论小模板

1 void div_fac(int m) 2 { 3 Len = 0; 4 for(int i=2; i*i<=m; i++) if(m%i==0) 5 { 6 p[Len] = i; 7 xc[Len] = 1; 8 while(m%i==0) xc[Len] *= i , m /= i; 9 Len++; 10 } 11 if(m>1) p[Len] = xc[Len++] = m; 12 } 13 14 int getcount(int x,int p) 15 { 16 int ret = 0; 17 while(x) 18 { 19 x /= p; 20 ret += x; 21 } 22 return ret; 23 } 24 25 int pow_mod(int a,int n,int mod) 26 {//快速幂 27 a%=mod; 28 int r = 1; 29 while(n) 30 { 31 if(n&1) r=(ll)r*a%mod; 32 a=(ll)a*a%mod; 33 n>>=1; 34 } 35 return r; 36 } 37 38 int gcd(int a,int b,int &x,int &y) 39 {//最大公因数 40 if(b==0) 41 { 42 x=1; 43 y=0; 44 return a; 45 } 46 int d = gcd(b,a%b,y,x); 47 y-=a/b*x; 48 return d; 49 } 50 51 int inv(int a,int mod) 52 {//求逆元 53 int x,y; 54 while( gcd(a,mod,x,y) != 1 ); 55 return (x+mod)%mod; 56 } 57 58 int crt(int a[],int m[],int n) 59 {//中国剩余定理 60 int M = 1; 61 for(int i=0; i<n; i++) M*=m[i]; 62 int ret = 0; 63 for(int i=0; i<n; i++) 64 { 65 int x,y,tm=M/m[i]; 66 gcd(tm,m[i],x,y); 67 ret=(ret+(ll)tm*x%M*a[i])%M; 68 } 69 return (ret+M)%M; 70 }
点hash

1 const int maxn=500+10; 2 const int prime = 100007; 3 4 pii pt[maxn]; 5 6 struct point_hash 7 { 8 int _hash[prime+5]; 9 int _next[prime+5]; 10 void clr() 11 {//清空hash表 12 cl(_next,0),cl(_hash,0); 13 } 14 void insert(pii pt,int index) 15 {//向hash表中插入标号是index的点pt 16 int x=pt.first,y=pt.second; 17 int h = (x*x+y*y) % prime; 18 int u = _hash[h]; 19 while(u) 20 { 21 u=_next[u]; 22 } 23 _next[index]=_hash[h]; 24 _hash[h]=index; 25 } 26 bool ok(pii p) 27 {//查询hash表中点p是否存在 28 int x=p.first,y=p.second; 29 int h = (x*x+y*y) % prime; 30 int u = _hash[h]; 31 while(u) 32 { 33 if(pt[u].first==x && pt[u].second==y)return true; 34 u=_next[u]; 35 } 36 return false; 37 } 38 }pthash;
威尔逊定理
p为素数时 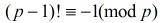
从ACdream那里扒下来的


1 #include <iostream> 2 #include <string.h> 3 #include <stdio.h> 4 #include <math.h> 5 6 using namespace std; 7 typedef long long LL; 8 9 int Work(LL n) 10 { 11 while(n % 4 == 0) n >>= 2; 12 if(n % 8 == 7) return 4; 13 LL i = 8, t = 9; 14 while(t <= n) 15 { 16 while(n % t == 0) n /= t; 17 i += 8; 18 t += i; 19 } 20 if(n == 1) return 1; 21 if(n % 2 == 0) n >>= 1; 22 if(n % 4 == 3) return 3; 23 LL k = 3; 24 while(k * k <= n) 25 { 26 if(n % k == 0) return 3; 27 k += 4; 28 } 29 return 2; 30 } 31 32 int main() 33 { 34 LL n; 35 while(cin>>n) 36 cout<<Work(n)<<endl; 37 return 0; 38 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号