计算机视觉基础4——对极几何(Epipolar Geometry)

　　先思考一个问题：用两个相机在不同的位置拍摄同一物体，如果两张照片中的景物有重叠的部分，我们有理由相信，这两张照片之间存在一定的对应关系，本节的任务就是如何描述它们之间的对应关系，描述工具是对极几何 ，它是研究立体视觉的重要数学方法。

　　要寻找两幅图像之间的对应关系，最直接的方法就是逐点匹配，如果加以一定的约束条件对极约束(epipolar constraint)，搜索的范围可以大大减小。

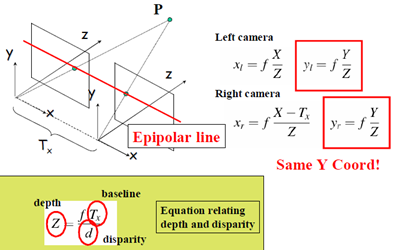
　　先回顾简单的立体成像系统

对极约束的图示

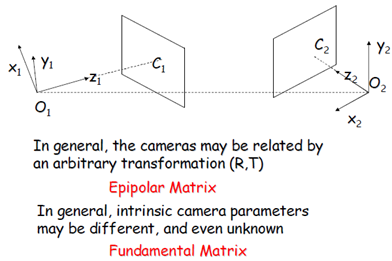
更一般的立体成像关系：两个相机的坐标无任何约束关系，相机的内部参数可能不同，甚至是未知的。要刻画这种情况下的两幅图像之间的对应关系，需要引入两个重要的概念——对极矩阵(Epipolar Matrix)和基本矩阵(Fundamental Matrix)。

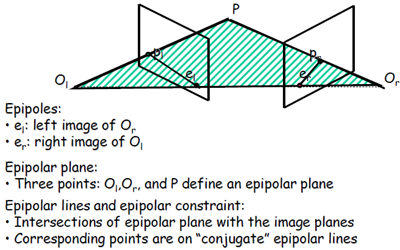
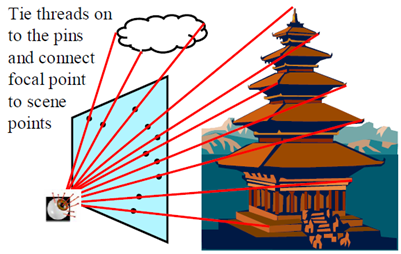
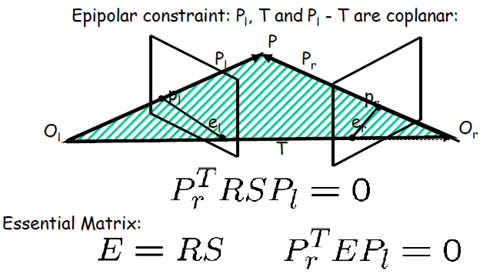
对极几何中的重要概念（参考下图）：

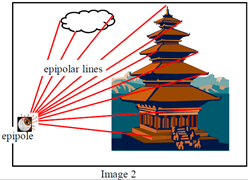
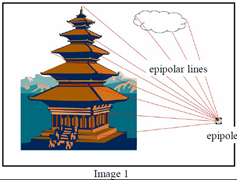
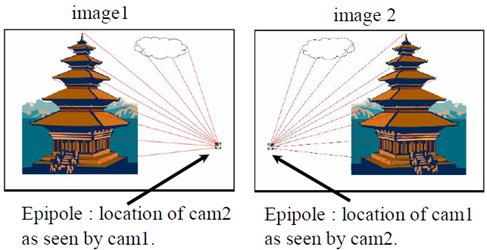
极点：极点$e_l$:右相机坐标原点在左像平面上的像；极点$e_r$:左相机坐标原点在右像平面上的像

极平面：由两个相机坐标原点$O_l$、$O_r$和物点P组成的平面

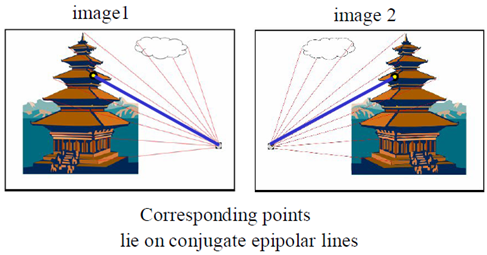
级线：极平面与两个像平面的交线，即$p_le_l$和$p_re_r$

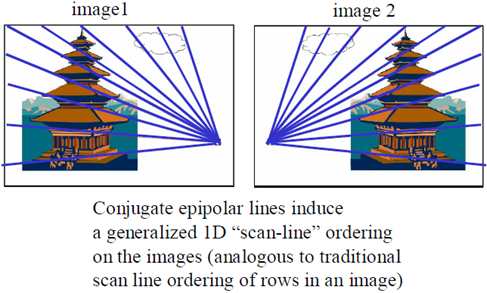
级线约束：两极线上点的对应关系

有点烦人，先转移一下话题：What would Pinhead’s eye look like close up?

如果两个人同时看这一景物，将是什么样的呢？

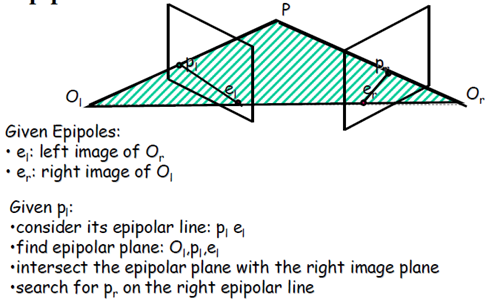
再回到对极几何图上来，通过上面几幅图示，利用对极几何的约束关系，我们可以：

1. 找到物点P在左像平面上的像点$ p_l $；

2. 画出极线$p_le_l $；

3. 找到极平面$ O_lp_le_l $与右像平面的交线，即得极线$p_re_r$；

4. 像点$p_l$的对应点一定在极一$p_re_r$上。

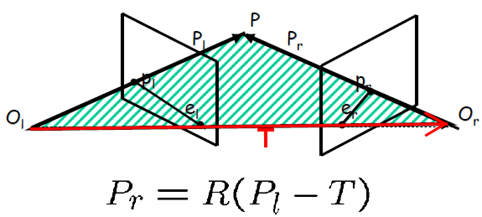
两个相机坐标系之间的关系为

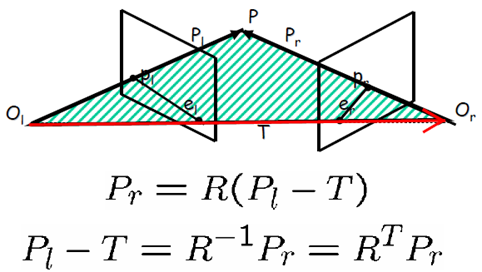
由于R是正交矩阵，因此可写为

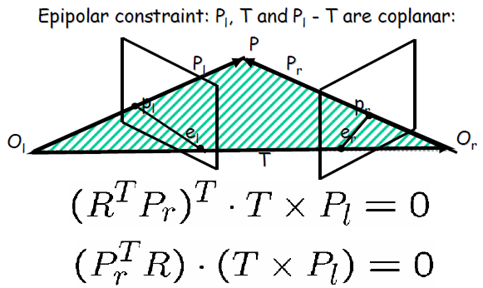
三向量共面，它们的混合积为零(混合积对应于有向体积)

将向量乘(叉乘)写成矩阵的形式

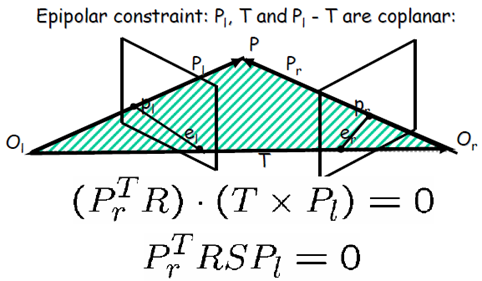
通过进一步的改写，可以得到左像点和右像点之间约束关系(非常简单、漂亮)

显然，左像点$p_l$和右像点$p_r$是通过矩阵$E=RS$来约束的，我们称矩阵$E$为本质矩阵(Essential Matrix)，它的基本性质有：

• has rank 2(秩为2)

• depends only on the EXTRINSIC Parameters (R & T)(仅依赖于外部参数R和T)

 

关于本质矩阵的性质，见下一节：立体视觉基础5——本质矩阵与基本矩阵