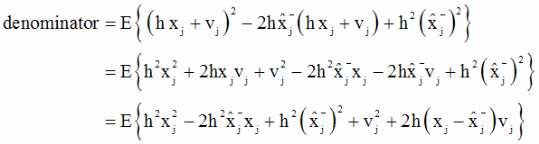标量Kalman滤波器
译:http://www.swarthmore.edu/NatSci/echeeve1/Ref/Kalman/ScalarKalman.html
该文档简单介绍输入为标量的卡尔曼滤波器的导出,分以下几节:
- 定义问题
- 寻找卡尔曼滤波器增益K
- 寻找先验方差
- 寻找后验方差
- 相关结果回顾
- 与常用符号记法的比较
- 例子
- 扩展
- 参考文献
定义问题
离散时间线性系统经常描述为如下状态方程:
式 1
其中,状态 $x_j$是标量,$a$和 $b$是常量,输入 $u_j$是一个标量;$j$是时间变量,注意,许多课本没有包括输入项(可视之为零),许多课本用变量 $k$表示时间,而我选择 $j$作为时间变量,因为在下文中 $k$用作卡尔曼滤波器增益。方程1图示如下,其中 $T$模块表示一个单位的延迟。
图 1
现在假设过程引入加性噪声:
式 2
噪声 $w$是均值为零方差为 $Q$的的白噪声,且与输入不相关。于是过程可描述如下:
图 2
对于如上述示的情形,一个典型的问题是:我们能否对信号 $x$进行滤波以便将噪声 $w$的影响减到最小?事实证明答案是肯定的。不过,利用卡尔曼滤波器,我们可以做得更多。
我们假设信号 $x$不能被直接测量,而可测量的是 $z$。
式 3
测量值 $z$依赖于 $x$的当前值,并由增益 $h$确定。另外,测量的自身噪声为 $v$。该噪声均值为零、方差为 $R$且与输入或噪声 $w$不相关。这两类噪声相互独立且与输入也独立。
图 3
卡尔曼滤波的任务现在可表述为:对于一个如上图所示的系统,我们怎么样对 $z$进行滤波来估计 $x$以使得 $w$和 $v$的影响最小?
要对状态(输出)进行估计,一种看似简单而合理的做法是复制系统结构,这种简单(根本无用)的方法可以得到 $x_j$的估计(记为 $\hat x_j$),图示如下:
图 4
这种方法有两个明显的缺点。首先,这里没有修正。如果我们无法确切知道量 $a,b$或者 $h$(或者初始值 $x_0$),估计值不会跟踪真实值 $x$。第二点,我们没有补偿加性噪声 $w$和 $v$。一种改进的措施是将两者考虑进去,如下图所示:
图 5
该图和前一个十分相似。注意到的第一个不同点是原来 $x_j$的估计现在记为 $\hat x_j^ - $;我们称之为先验估计。
式 4
我们用这个先验估计去预测输出,即输出的估计 $\hat z_j$。输出的真实值和其估计之间的差称为残差,或新息。
式 5
如果残差较小,通常意味着我们的估计较好;如果残差较大,则说明估计不好。我们可以用这一信息来改善我们对 $x_j$的估计;我们称新的估计为后验估计 $\hat x_j$。如果残差较小,则对估计的修正也较小。当残差增大时,修正也增大。相关的方程是(根据框图):
式 6
目前唯一的任务就是寻找用来改善我们估计的量 $k$,这一过程是卡尔曼滤波的核心。
注意:我们试图寻找最优的估计,目前我们只优化增益 $k$的值。我们已经假设原系统的拷贝(即增益 $a,b$ 和 $h$分布如图所示)用来进行估计。这样自然会提出一个问题:“这样得到的估计是最优的吗?”换句话说,为了估计状态,我们简单地拷贝原来的系统,或者还有更好的办法?如上所示,这样的估计被证明是最优线性估计。详见这里。
寻找卡尔曼滤波器增益K
开始之前定义估计误差。这里有两类误差,一类是先验误差 $e_j^-$,另一类是后验误差 $e_j$。每一类误差都是真实值 $x_j$与估计(先验或后验)的差值。
式 7
与每一类误差相关的均方差或方差:
式 8
其中运算符E{ }表示期望或平均值。这些定义将用于计算 $k$值。
卡尔曼滤波是通过选择适当的 $k$值来最小化后验误差 $p_j$。我们先将式7代入式8,之后再代入式6。
式9
为了求解最小化方差的 $k$值,对表达式关于 $k$求导并令其为零。要有耐心,化简之前,表达式有点复杂。
式 10
我们用最后一个式子来求解 $k$。
式 11
这个表达式依然比较复杂。简单起见,我们分别考虑分子和分母。
我们先看分子,将3式表示的 $z_j$代入其中。
测量噪声 $v$与输入及 $x$的后验估计都不相关,所以:
式 12
分子简化为:
式 13
同理,考虑分母。
我们再次利用式12的正交条件,最后一项为零,所以:
式 15
其中,上式中我们用了式13来化简第一项,而第二项是测量噪声的定义。
利用分子分母表达式,我们最终得到一个简化的式子 $k$:
式 16
然而,依然存在一个问题,因为表达式中需要一个先验方差的值,反过来,它需要知道系统变量 $x_j$。因此,我们下一步任务就是先验方差的估计。
开始之前,让我们仔细看看上式。 首先,$k$不是常量,每次迭代都会改变。正因如此,在书写时应该加个下标(即 $k_j$)。下文中我们要格外注意这点。
接下来,更重要的是我们考查当式16中的每一项改变时将发生什么。
$\bullet $如果先验误差很小,相应地,$k$也很小,所以我们的校正也很小。换句话说,我们可以忽略当前的测量值并用之前的估计作为新的估计。正如所希望的那样——如果我们最初的估计(先验估计)很好(即误差小),则仅需很小的修正。
$\bullet $如果先验误差很大(这样的话,分母中的测量噪声项 $R$将无足轻重),于是 $k=1/h$。实质上告诉我们丢弃先验估计而用当前(测量)输出值来估计状态。代入6式可以清楚地看出这一点。另外,正如所希望的那样——如果先验误差很大,我们应该丢弃先验估计,而应该用当前测量的输出值来估计状态。

$\bullet $如果测量噪声 $R$很大,$k$就会很小,所以我们丢弃当前的测量以得到新的估计。正如所希望的那样——如果测量噪声大,则测量值的可信度低,于是估计值应更多地依靠先前的估计。
寻找先验方差
根据定义直接可以得到先验方差。
由前述可知,中间项可以去掉,因为过程噪声与前一时刻状态及其先验估计都不相关。
式 17
所以
式 18
然而并未结束,因为我们还需要后验估计 $p_j$。
寻找后验方差
与先验方差类似,我们通过其定义来寻找后验方差。
式 19
由前述可知,中间项可以去掉,因为测量噪声与当前状态及其先验估计不相关。
式 20
所以
式 21
通过 $k$的定义(式16的变形)我们可以简化上式
式 22
将式22代入式21得到
式 23
相关结果回顾
任何卡尔曼滤波操作都是从系统描述开始,其中包括增益 $a,b$和 $h$,状态 $x$,系统输入 $u$,输出 $z$,时间索引 $j$。
该过程有两个阶段,预测阶段(仅依靠之前输出的测量值去计算下一状态的估计值),修正阶段(用当前估计值去改善预测的结果)。
预测阶段
我们用前一时刻状态的估计与当前的输入来得到(当前)状态的先验估计。
我们现在可以计算先验方差
注意到以上两式用到前一时刻状态的后验估计和方差。因此卡尔曼滤波的首次迭代时要求这两个值的估计(通常只是猜测)。确切的估计往往并不重要,因为随着时间的推移,会收敛到正确的值。一个不好的的初始估计只是会导致收敛的时间更长。
修正阶段
为了修正先验估计,我们需要用到卡尔曼滤波器增益 $k$。
该增益用于改善(修正)先验估计并使我们得到后验估计。
现在我们可以计算后验方差
关于卡尔曼滤波器增益 $k_j$的说明
$\bullet $如果先验误差很小,$k$相应地也很小,所以修正也很小。换句话说,我们可以忽略当前的测量而仅用过去的估计作为新的估计。正如所希望的那样——如果我们最初的估计(先验估计)很好(即误差小),则仅需很小的修正。
$\bullet $如果先验误差很大(这样的话,分母中的测量噪声项 $R$将无足轻重),于是 $k=1/h$。实质上告诉我们丢弃先验估计而用当前(测量)输出值来估计状态。代入6式可以清楚地看出这一点。另外,正如所希望的那样——如果先验误差很大,我们应该丢弃先验估计,而应该用当前测量的输出值来估计状态。
$\bullet $如果测量噪声 $R$很大,$k$就会很小,所以我们丢弃当前的测量以得到新的估计。正如所希望的那样——如果测量噪声大,则测量值的可信度低,于是估计值应更多地依靠先前的估计。
与常用符号记法的比较
本文档符号的记法参考[1]。更常用的记法如下。
| 变量 | 该文档中的记法 | 通常记法 |
| 时间变量 | j | k |
| 状态 | xj | x(k) |
| 系统增益 | a, b, h | a, b, h (注意:b通常为0) |
| 输入 | uj | u(k) (注意:通常没有输入) |
| 输出 | zj | z(k) |
| 增益 | kj | Kk |
| 先验估计 |  | |
| 后验估计 |  | |
| 先验方差 | p- | p(k|k-1) 或 p(k+1|k) |
| 后验方差 | pj | p(k|k) 或 p(k+1|k+1) |
记法
可以读作“基于时刻 $k-1$的信息对时刻 $k$时状态 $x$的估计”;换句话说,该估计仅依赖过去的输出,或先验估计。记法
可以读作“基于时刻 $k$的信息对时刻 $k$时状态的估计”;换句话说,该估计依赖过去和当前的输出,或后验估计。
例子
扩展
参考文献
[1] An Introduction to Kalman Filters, G Welch and G Bishop, http://www.cs.unc.edu/~welch/kalman/kalman_filter/kalman.html. See also their other introductory information on Kalman Filters.
[2] Handbook of Digital Signal Processing, D Elliot ed, Academic Press, 1986.
[3] Digital and Kalman filtering : an introduction to discrete-time filtering and optimum linear estimation, SM Bozic, Halsted Press, 1994.
[4] An Engineering Approach to Optimal Control and Estimation Theory, GM Siouris, John Wiley & Sons, 1996.
[5] Statistical and Adaptive Signal Processing, DG Manolakis, VK Ingle, SM Kogon, McGraw Hill, 2000.
[6] Smoothing, Filtering and Prediction - Estimating The Past, GA Einicke, a free on-line text:http://www.intechopen.com/books/smoothing-filtering-and-prediction-estimating-the-past-present-and-future