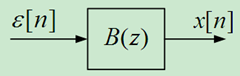滤波器设计、谱分解及信号模型
不同学科之间,在某些不同的问题中,蕴涵的本质可能是相同或相似的。而在相同的学科中,问题之间的联系将更加紧密。在此,我想将经典数字信号处理和现代数字信号处理中两个看似不相关的问题作一些对比,并试图突出它们之间的共性。
滤波器设计
滤波器基本理论及设计方法是经典数字信号处理课程的核心内容。广义上讲,任何能对某些频率(相对于其它频率来说)进行修正的系统都可称之为滤波器。最常规的分类方法是根据单位脉冲 $h[n]$的特点分为有限长单位脉冲响应FIR(Finite Impulse Response)滤波器和无限单位脉冲响应IIR(Infinite Impulse Response)滤波器,而从相位特性角度来看,又可分为线性相位和非线性相位滤波器,一般而言(存在一些特殊结构),IIR滤波器不具备线性相位,而FIR可以(而非一定)具有严格线性相位。
滤波器的设计一般包括以下三个步骤:
- 给出系统所要求特性的技术指标;
- 用因果离散时间系统逼近这些技术指标;
- 实现该系统。
步骤1主要取决于应用场合,而步骤3则取决于实现滤波器时所用的技术。在滤波器设计中,我们的注意力主要集中于步骤2。
对于步骤1,从滤波器频率特性而言,应该包括幅频特性和相频特性,而在实际中,通常只给出幅频特性的要求,如截止频率、过滤带宽度及阻带衰减等。难道相频特性不重要吗?当然不是,之所以不显式地要求,原因是在某些约束条件下,幅频特性可以唯一地决定相位特性,或者在先满足幅频特性的要求之下,可以通过级联全通系统来改变相位特性以满足相位要求。那么,某些约束条件是指什么呢?这得从幅度和相位之间的关系说起
幅度和相位之间的关系
用来描述一个线性时不变系统的参数有很多,在时域中,用单位脉冲响应 $h[n]$可以完全描述,在频率中用频率响应 $H(e^{j\omega})$,当然,也可以用系统函数 $H(z)$(别忘了结合收敛域)。而在滤波器设计过程中,一般给出频率指标要求,主要是幅频特性,但通常情况下,关于幅度特性的信息并不能给出任意有关相位特性的信息;反过来也一样。然而,对于由线性常系数差分方程描述的系统,也即具有有理系统函数的系统,其幅度和相位特性之间有某种约束关系存在。特别是,如果频率响应的幅度特性和零极点个数是已知的话,那么与其有关的相位特性仅有有限种选择。类似地,如果零极点个数和相位特性已知的话,那么除了一个幅度加权因子外,也仅有有限个幅度特性可供选取。再者,在最小相位的限制下,频率响应的幅度特性唯一地决定了相位特性;而频率响应的相位特性除去一个幅度加权因子外也决定了幅度特性。(具体证明后续给出)
滤波器设计的根本任务
尽管滤波器设计及其实现是本科数字信号处理教学的核心,但采取什么方式可以言简意赅地叙述清楚一直是个难题,本质的问题容易淹没在细枝末节中。那么,滤波器设计的最本质问题是什么呢?简单地讲,就是寻找一组满足技术指标的参数?什么参数?这取决于描述LTI(线性时不变)系统的方式,回到最初的建模阶段,通常是用线性常系数差分方程来描述离散时间LTI系统:
\[\sum\limits_{k = 0}^N {{a_k}y[n - k] = } \sum\limits_{m = 0}^M {{b_m}x[n - m]}\;\;\;\;\; (1) \]
很显然,在上述方程中,参数包括 $ N$(称为方程的阶次)、 $M$、 $ a_k$和 $b_m$,这四个(类)参数可唯一确定方程,因此,滤波器设计的最根本任务就是确定这四个(类)参数,但对于用户或客户而言(假设客户让你设计滤波器),他提技术指标时肯定不是对这四个(类)参数)而言,通常是我们“需要将50Hz的干扰去除”、“1kHz 以上的频率成分滤除”等等,这些要求似乎和差分方程的四个(类)参数风牛马不相及,而建立这两者之间的联系是我们学习的重点,教材质量的好坏、老师教学能力的高低基本上可以在此处得以体现。
先要解决第一个问题。数字滤波器幅频响应 $H(e^{j\omega})$描述的是频率和滤波器幅度之间的关系,频率变量是 $\omega$,称为数字角频率,与之对应的当然就是模拟角频率 $\Omega$,两者有什么关系呢?假设有一个模拟正弦(此处不区分正弦和余弦)信号 $\cos\Omega t$,对其进行均匀采样,采样间隔为 $T$,即在 $t = nT$的时刻取得样值,其中 $n$为整数,采样之后的信号便是离散正弦序列 $\cos \omega n$,于是有
\[ \cos \omega n = \cos \Omega nT \]
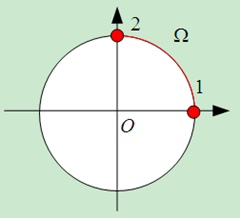
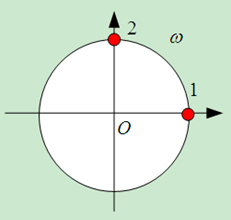
对比等式两端,易得 $\omega = \Omega T = \Omega/f_s $,其中 $f_s = 1/T$称为采样频率,这是模拟信号转化为数字信号时极其重要的一个参数。根据等式 $\omega =\Omega/f_s $得出一个重要结论:数字频率是模拟频率关于采样频率的归一化,这就像地图册一样,地球再大,我们可以画在一张A4的纸上,相比之下,一个小城镇也可以画在一张A4纸上,如何比较或者确定地球和小城镇的实际大小呢?比例尺!因此,采样频率就相当于比例尺,对模拟频率进行归一化。“归一化”,顾名思义,就是回归到1以内,最大值不超过1,就像地图册一样,再大也不能超过A4的纸,那么,用采样频率对模拟频率进行归一化所得到的数字频率 $\omega$的范围是多少呢? $-\pi \sim \pi $。如何理解?首先搞清楚 $\Omega$ 和 $\omega$的量纲,前者是弧度/每秒,后者是弧度/样点,有什么区别?对比以下两幅图,假设有一只蚂蚁,在时刻0时处于位置1,沿着圆周爬行,在时刻 $t$处在位置2,如果你睁着眼睛一直盯着,蚂蚁走过的所有轨迹你都能观察到,这就对应图1的情况,即你的观察是连续的,此时蚂蚁运动的角频率就是 $\Omega = \pi /(4t)$弧度/秒;而图2的情况相当于在时刻0时,你睁开眼睛观察一下,发现蚂蚁在位置1,立马闭上双眼(即相当于观察的时间长度为0),再过时间 $t$之后,再一次睁开眼睛观察一下,发现蚂蚁在位置2,在这种情况下如果问你:蚂蚁是如何到达位置2的呢?逆时针?顺时针?旋转了 $\pi /4$? $3\pi /4$?还是绕了若干圈?如果不加以限制,这个问题就没有唯一解。加上什么限制,这个问题的解是唯一的呢?直观地想,如果我们相邻再次睁眼的时间间隔比较短,特别地,如果已知在蚂蚁运动一圈的时间内,保证至少睁眼两次(当然假设蚂蚁的运动是匀速的,睁眼的间隔也是均匀的),这样就中会引起多解了,因为如果时刻0(第一次睁眼)处于位置1,时刻 $t$(第二次睁眼)处于位置2,不仅可以确定蚂蚁的运动方向,而且也能确定蚂蚁在相邻两次观察中旋转的角度,即 $(\pi / 4)$/样点。上述的限制条件其实就是我们熟知的Nyquist采样条件。有了这个限制条件,数字频率的取值范围就是 $-\pi \sim \pi $(逆时针对应正,顺时针对应负)。这就是在频率中分析离散时间系统时,只关心 $-\pi \sim \pi $的频率范围,由于频率响应的 $2\pi $周期性,为了分析的方便,有时候也限制在 $0 \sim 2\pi$的范围。
图1 连续时间(模拟)爬行 图2 离散时间(数字)爬行
再回到 $\omega =\Omega/f_s $,可以看出,联系模拟频率和数字频率的桥梁是采样频率 $f_s$,如果要从数字频率“返回”模拟频率,就必须要有一个对应关系,如上所言,数字频率的范围是 $0 \sim 2\pi$,而数字频率又是模拟频率对采样频率的归一化,显然有最大的数字频率对应采样频率 $f_s$(归一化嘛,就将最大的模拟频率 $f_s$归成为最大的数字频率)。这样就解决了第一个问题——模拟频率和数字频率的映射关系。因为滤波器的技术指标往往是在模拟域中给出的,而数字滤波器的设计又是在数字域中完成的,因此掌握两者的映射关系至关重要。当然,在数字滤波器设计过程中因技术需要,模拟频率和数字频率的映射关系可能会不同,另当别论。
如何从幅频响应 $|H(e^{j\omega})|$开始
一定不要忘记滤波器设计的最根本任务:确定线性常系数差分方程的那四个(类)参数。对于给定的频率技术指标——幅频响应$|H(e^{j\omega})|$,如何建立它们之间的联系呢?系统函数起着桥梁作用。为了阐明在给定系统频率响应的幅度平方特性下,系统函数的可能选择,考虑将 $|H(e^{j\omega})|^2$表示成
\[ |H(e^{j\omega})|^2= H(e^{j\omega})H^*(e^{j\omega}) = H(z)H^*(1/z^*)|_{z=e^{j\omega}} \;\;\; (2)\]
由差分方程(1)确定的系统函数具有有理形式,即
\[ H(z) = \frac{{{b_0}}}{{{a_0}}}\frac{{\prod\limits_{k = 1}^M {\left( {1 - {c_k}{z^{ - 1}}} \right)} }}{{\prod\limits_{k = 1}^N {\left( {1 - {d_k}{z^{ - 1}}} \right)} }} \;\;\; (3)\]
那么,式(2)中的 $H^*(1/z^*)$就是
\[{H^*}\left( {\frac{1}{{{z^*}}}} \right) = \frac{{{b_0}}}{{{a_0}}}\frac{{\prod\limits_{k = 1}^M {\left( {1 - c_k^*z} \right)} }}{{\prod\limits_{k = 1}^N {\left( {1 - d_k^*z} \right)} }} \;\;\; (4) \]
这里已经假设 $a_0,b_0$都是实数。因此式(2)就意味着该频率响应的幅度平方就是由下式给定的 $z$变换 $C(z)$在单位圆上的求值:
\[C(z) = H(z)H^*(1/z^*) = {\left( {\frac{{{b_0}}}{{{a_0}}}} \right)^2}\frac{{\prod\limits_{k = 1}^M {\left( {1 - {c_k}{z^{ - 1}}} \right)\left( {1 - c_k^*z} \right)} }}{{\prod\limits_{k = 1}^N {\left( {1 - {d_k}{z^{ - 1}}} \right)\left( {1 - d_k^*z} \right)} }} \;\;\; (5)\]
如果已知 $|H(e^{j\omega})|^2 $,那么以 $z$代替 $e^{j\omega} $就能构造出 $ C(z)$,有了 $C(z)$,能唯一确定系统函数 $H(z)$吗?如果能,由于有理形式的 $H(z)$与差分方程一一对应,也就是说,$H(z)$可以唯一确定差分方程,一旦差分方程确定了,那四个(类)参数也随之确定,这样一来,滤波器设计的根本任务也就完成了。不幸的是,一般情况下,由 $C(z)$不能唯一确定系统函数 $H(z)$,从式(5)可以看出,对于 $H(z)$的每个极点 $d_k$,在 $C(k)$中就会有 $d_k$和 $(d_k^*)^{-1}$的极点存在。类似地,对于 $H(z)$的每个零点 $c_k$,在 $C(k)$中就会有 $c_k$和 $(c_k^*)^{-1}$的零点存在。因此, $C(z)$的零极点是以共轭倒数的形式出现的,每对中的一个是与 $H(z)$相联系的,另一个则与 $H^*(1/z^*)$有关。再者,如果每对中的一个是在单位圆内的话,那么另一个(即共轭倒数)就一定在单位圆外。仅有的例外是这两个都在单位圆上,那么它们就在同一位置上。如果不加任何限制,在共轭倒数的零、极点中,任取一半零、极点分配给 $H(z)$,而另一半给 $H^*(1/z^*)$都对应同一个 $C(z)$。
如果 $H(z)$ 假设是对应于一个因果稳定的系统,那么它们的全部极点都必须位于单位圆内。有了这个限制, $H(z)$的极点可以从 $C(z)$的极点中分离出来。然而,仅凭这一点, $H(z)$的零点还是不能从 $C(z)$的零点中唯一地被确定。如果再加上限制条件:这个因果稳定的系统还是最小相位的,即要求所有 $H(z)$的所有零点也在单位圆内。此时,由 $C(z)$便可唯一确定 $H(z)$了。
总结一下:在滤波器设计中,一般在频域中给出幅频特性的技术指标,如果是模拟频域,则先转换为数字频域,即得到数字频域中的幅频响应 $|H(e^{j\omega})|$,由 $|H(e^{j\omega})|$可以构造出 $C(z)$,加上限制条件“所设计的滤波器是因果稳定的最小相位系统”,则将 $C(z)$单位圆内的零点和极点分配给 $H(z)$(如果零极点在单位圆上,任意选一半即可),这样一来,系统函数 $H(z)$被唯一确定下来,等价地,那四个(类)参数被唯一确定下来,从而完成了滤波器设计的根本任务。
谱分解和信号模型
在分析随机信号时,由于没有确定的表达式,且能量无限,因此无法像分析确知信号那样直接利用傅里叶变换,往往从它的数字特征入手研究其特性,如相关函数和均值。均值容易理解,下面重点说说自相关函数。
离散时间实平稳随机信号 $x[n]$的自相关函数定义为
\[{R_{xx}}[k] = E\{ x[n]x[n + k]\} \]
$x[n]$的功率谱 $S_{xx}(z)$定义为 $x[n]$自相关函数的双边 $z$变换,即
\[{S_{xx}}(z) = \sum\limits_{k = - \infty }^\infty {{R_{xx}}[k]{z^{ - k}}} \]
若 $R_{xx}[k]$是稳定的,则 $S_{xx}(z)$的收敛域包括 $z$平面上的单位圆,于是令 $z=e^{j\omega}$,便可定义以频率为自变量的功率谱
\[{S_{xx}}(z) = \sum\limits_{k = - \infty }^\infty {{R_{xx}}[k]{z^{ - k}}} \]
$S_{xx}(\omega)$在物理意义上说明了信号 $x[n]$的频率成分,以及功率随频率的分布。
对于实平稳随机信号,用统计的方法,我们可以求得功率谱,进而可以求得自相关函数 $R_{xx}[k]$。如果能由自相关函数进一步得到随机信号 $x[n]$就好了。这个问题和“滤波器设计”一节中提到的根据 $C(z)$确定 $H(z)$一样,如果加上一定的限制,则也可以由功率谱 $S_{xx}(z)$唯一确定随机信号(序列)。根据自相关函数和功率谱的定义有
\[{R_{xx}}[k] = \sum\limits_{k = - \infty }^\infty {x[n]x[n + k]} = x[ - k]*x[k] \Leftrightarrow {S_{xx}}(z) = X({z^{ - 1}})X(z) \;\;\;\; (6) \]
对比式(5)和式(6),在本质上讲是一样的,即如何根据 $C(z)$或者 $S_{xx}(z)$确定 $H(z)$或者 $X(z)$。如前所述,如果要求随机信号(序列) $x[n]$是最小相位序列,则将功率谱 $S_{xx}(z)$分解为 $X(z^{-1})X(z)$是唯一的,这就是谱分解定理,正式表述如下:
谱分解定理 任何实平稳随机信号 $x[n]$的有理功率谱 $S_{xx}(z)$都可唯一地表示成下列最小相位形式
\[{S_{xx}}(z) = {\sigma ^2}B(z)B({z^{ - 1}}) \;\;\;\; (7)\]
式中,$\sigma^2$为常系数, $B(z)$是有理函数,即
\[B(z) = \frac{{N(z)}}{{D(z)}}\]
式中,$N(z)$和 $D(z)$都是最小相位多项式。适当调整常数系数 $\sigma^2$的数值,以使 $N(z)$和 $D(z)$都是最高次系数为1的多项式,这样式(7)的分解就是唯一的。
谱分解定理保证了平稳随机信号模型的存在。任何平稳随机信号 $x[n]$可以看成是由白噪声序列 $\left\{ {{\varepsilon [n]}} \right\}$激励一个因果和稳定的线性时不变系统 $B(z)$产生的输出。因为对比式(6)和式(7)有 $X(z)=\sigma B(z)$,由于白噪声的 $z$变换是一常数,故如果将 $\left\{ {{\varepsilon [n]}} \right\}$的 $z$变换看成 $\sigma$,则平稳随机信号 $x[n]$的模型如下图所示:
总结:在滤波器设计和谱分解中都引入了最小相位的约束条件,前者是经典数字信号处理的内容,而后者是现代数字信号处理的内容,然而在本质上两者并无区别,特别地,谱分解定理保证了随机信号模型的存在,这是随机信号处理理论中的一个重大发现。