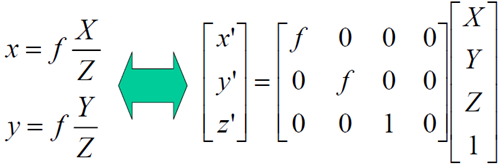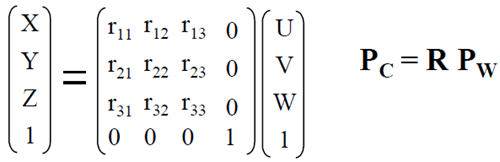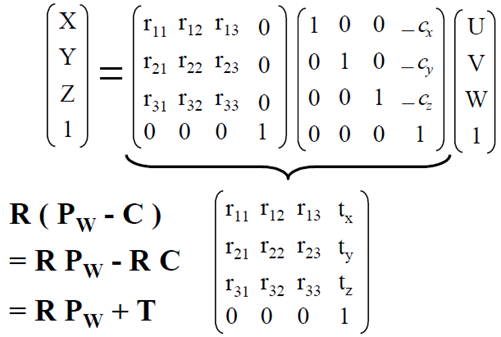计算机视觉基础2——相机成像的几何描述

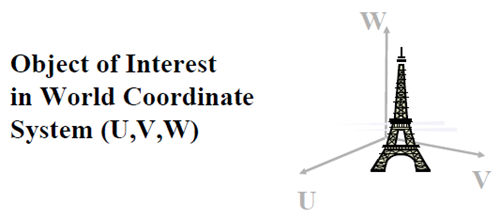
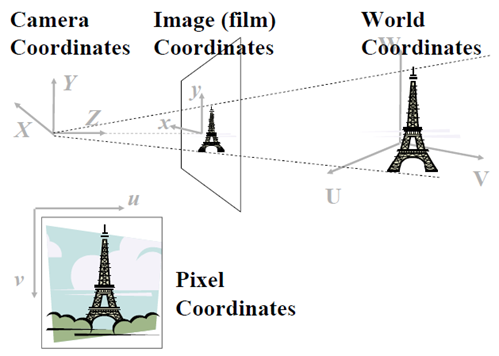
    试想像一下，很多游客同时在不同角度拍摄Eiffel Tower(埃菲尔铁塔)，该如何用数学的方法来描述这一过程呢？首先要解决的问题就是定位，或者说坐标选定的问题，埃菲尔铁塔只有一座，如果按经、纬度来刻画，它的坐标是唯一确定的，但游客显然不关系这一点，他(她)只按自己的喜好选择角度和位置，因此，物体(景物)有物体的坐标系统，相机有相机的坐标系统，即便同一个相机，当调整参数时，在同样的位置、相同的角度，也可能得到不同的图像。为了统一描述，有必要引入世界坐标(或物体坐标)、相机坐标和像平面坐标。

世界坐标用UVW记。

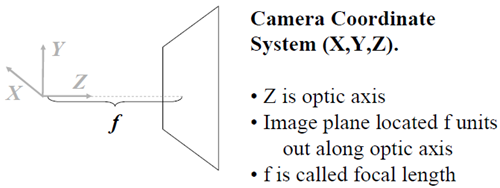
相机坐标用XYZ记。中学物理告诉我们，物体与像是倒的关系，但作为数学分析，我们采用虚像。像平面用xoy记。

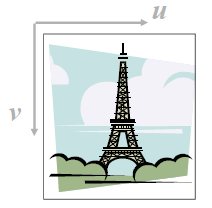
而数字图像用(u,v)来表示，不弄混淆像平面和数字图像这两个概念，同一个像通过平移、拉伸等，可以得到不同的数学图像(u,v)。

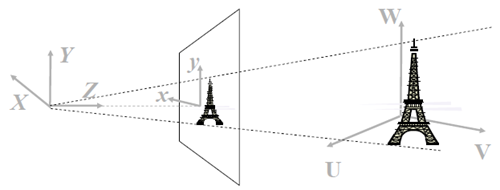
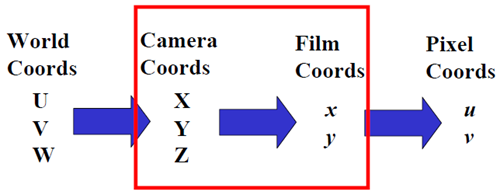
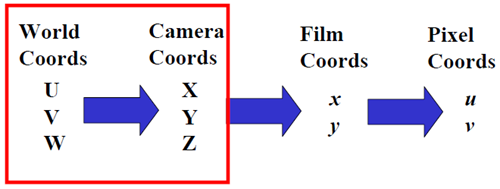
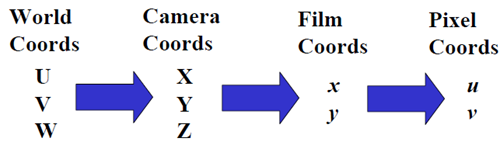
总体来看，就是

我们需要用数学的语言来描述这一过程。先看中间部分。

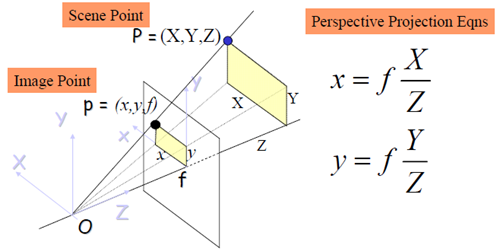
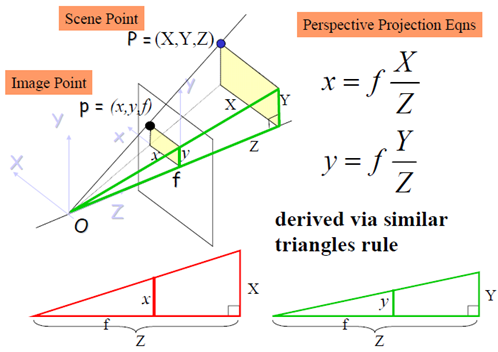
红框标注的部分是3D物体到2D像平面的透视投影(如果不明白透视投影的概念，需要补一下高等几何)

显然，OP上的任一点的像都是p(x,y)，为了描述这一关系，需要引入齐次坐标。

By convention, we specify that given (x’,y’,z’) we can recover the 2D point (x,y) as

$ x=\frac{x^'}{z^'} $     $ y=\frac{y^'}{z^'}  $    

Note: (x,y) = (x,y,1) = (2x, 2y, 2) = (k x, ky, k)

关于齐次坐标，更详细的介绍可参考高等几何。

上述透视投影的过程可以描述为

正如开头所言，不同游客会选择不同的位置和角度拍摄同一物体，因此，物体对于相机的关系各不相同，这就是物体到相机坐标变换的问题。

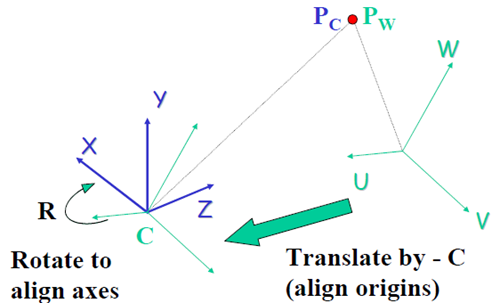
上述红框部分描述的是从物体的坐标(称为世界坐标)到相机坐标变换的过程，它是一种刚体运动，可以用平移、旋转来描述。

上图表示的是从世界坐标变换到相机坐标：$ P_c=R(P_w - C) $，写成矩阵形式

平移是容易理解的，我们先讨论更简单的情形，即假设世界坐标系和相机坐标系的原点重合，则变换只剩下旋转了。

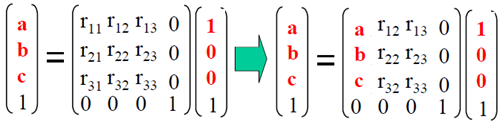
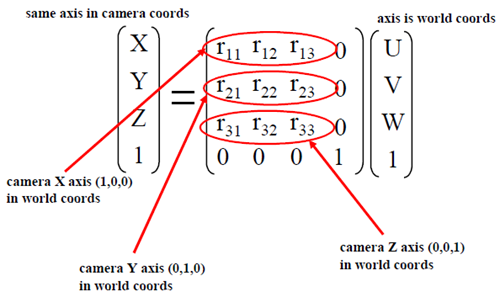
旋转矩阵的元素也很容易确定。试想(U,V,W)=(1,0,0)，而它在相机坐标系中的坐标是(X,Y,Z)=(a,b,c)(同一物理点的不同坐标)则有：

因此有：

由于该旋转是刚体运动，因此它是正交变换，满足$ R^{-1}=R^T $，所以有：

不难得出：

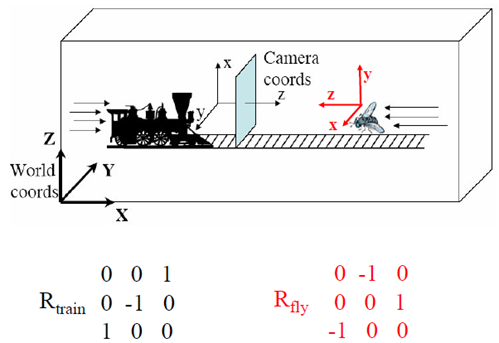
看一个例子：

由于物体的坐标到相机坐标的变换，相对于相机内部参数而言属于外部参数(External Parameters)，往往写作R和T，即

总结

本小节讲述了如何将3D世界坐标系中的点变换到相机坐标系中，然后经透视投影，变成2D像平面上的点(x,y).

下一节：立体视觉基础3——内部参数描述