「双端队列BFS」电路维修

本题为3月23日23上半学期集训每日一题中B题的题解

题面

题目描述

Ha'nyu是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女Rika，从而被收留在地球上。Rika的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个R行C列的网格（ \(R,C \leq 500\) ），如右图所示。每个格点都是电线的接点，每个格子都包含一个电子元件。电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后，它就可以连接另一条对角线的两个接点。电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

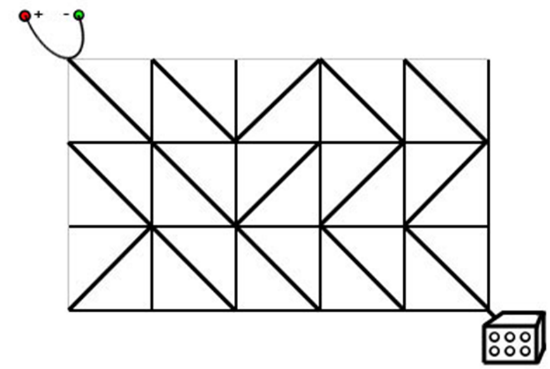
Ha'nyu发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。不过，电路的规模实在是太大了，Ha'nyu并不擅长编程，希望你能够帮她解决这个问题。

输入

输入文件包含多组测试数据。第一行包含一个整数T 表示测试数据的数目。

对于每组测试数据，第一行包含正整数R 和C，表示电路板的行数和列数。

之后R 行，每行C 个字符，字符是"/"和""中的一个，表示标准件的方向。

输出

对于每组测试数据，在单独的一行输出一个正整数，表示所需的缩小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出NO SOLUTION。

样例输入

1
3 5
\\/\\
\\///
/\\\\

样例输出

1

提示

样例的输入对应于题目描述中的情况。

只需要按照下面的方式旋转标准件，就可以使得电源和发动机之间连通。

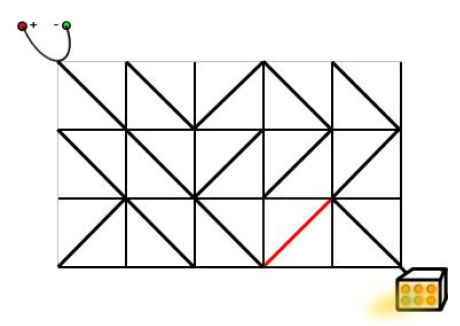
思路分析

本题要求的是转弯数的最小值,在图论中我们常常可求路径的最小值,所以我们尝试把旋转次数定义为"路径长",那么本题题意可以转化为,当从一个点移动到另一个点时,如果电路本身是通的,边权为0,否者边权为1,求起点到终点的最短路径.

转化后的此题类似于洛谷上第4554题的升级版,我们可以使用同样的思路解决此问题,即双端队列BFS(有人也叫它01BFS).

关于双端队列BFS,我之前一道题目的题解中从用来解最短路问题的BFS的角度出发进行过详细的分析,感兴趣可以去看一看,在这里我从Dijkstra算法的角度对它进行一些另一个视角的分析,相信你将会发现各个最短路算法之间的高度统一性.

我们知道,Dijkstra算法的贪心策略是,每次选择当前未确定的点中到起点距离最短的点,从这个点出发继续进行操作.而为了减少这个找最小值过程所花费的时间,我们采用优先队列进行优化.

此题当然也可以直接用Dijkstra算法来解决,因为此题没有负权边.但是我们其实没有必要完完全全按照Dijkstra算法来进行操作.我们注意到此处边权只有0和1,如果我们当前队列中是有序存放的,那么加上0边权之后,它依旧是最短的,我们可以直接把它放到队头;而加上1边权之后,又如何呢?由于队列是有序的,且边权是0和1,而加上0边权的全部放到了队首,加了1边权的一定会在0边权的全部处理完之后才会处理.所以队列里面同时一定只存在两种路径长度,且这两种长度差距一定是1.所以当前加上1边权之后,我们可以直接把它放到队尾.而初始的时候,队列里面只有起点到起点的距离(0),这是有序的(虽然只有一个元素,但是你就说它有序不有序吧),所以我们可以按照上述的方式来维护距离,即:

• 如果当前边权是0,我们把它放到队首
• 如果当前边权非0,我们把它放在队尾

由此,我们可以把优先队列换成一个双端队列,来优化掉优先队列的对数时间(你不会以为优先队列是常数时间吧?不会吧不会吧?).此时我们所写的这种最短路算法,就称之为双端队列BFS.所以从对Dijkstra算法优化的角度来看,所谓双端队列BFS就是在图上边权只有两种,且一种为0时的特殊优化.因为此时通过一定的操作,可以手动维护队列有序,所以可以优化掉那个需要log时间的优先队列,来减少时间消耗.

所以此题如何求解答案(即最短路)的方法已经确定了,我们只要把Dijkstra算法中插入优先队列的过程换成上面那两条规则即可.接下来我们的问题就是,如何确定边权.根据题目意思,格点对应的是图上的点,而点只能斜向移动到另一个点.所以我们只要看当前点向四个斜方向的边是什么形状即可.这里有一个难点是如何确定边的坐标,其实画一个图就很清晰了:

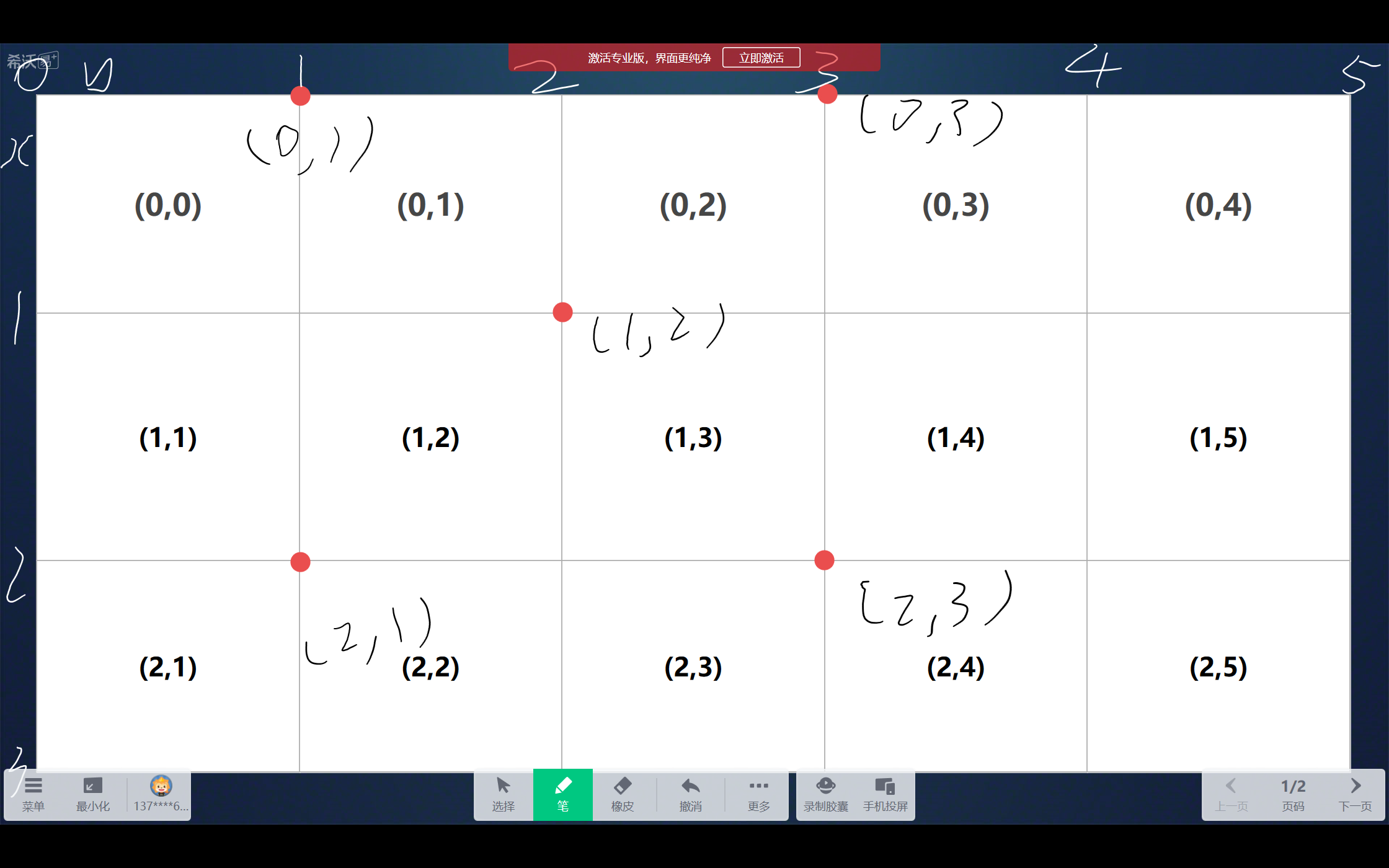
四个方向的坐标变换就是(1,1),(-1,1),(1,-1),(-1,-1),如果记原本的点坐标为(_x,_y),变换后的点坐标为(x,y),对应的边的坐标就分别是(_x,_y),(x,_y),(_x,y),(x,y),我们直接套用这个规律即可.

参考代码

时间复杂度: \(O(RC)\)

空间复杂度: \(O(RC)\)

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>

using namespace std;

using i64 = long long;

int book[][2] = {{1, 1}, {-1, 1}, {1, -1}, {-1, -1}}; // 对角线四个方向

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        int r, c;
        cin >> r >> c;

        vector<string> g(r); // 存边的形状
        for (auto &i : g) {
            cin >> i;
        }

        // 双端队列BFS(改造优先队列优化BFS,无注释的部分为Dijkstra本身的内容)
        deque<pair<int, int>> deq; // 双端队列(代替优先队列)
        vector<vector<int>> dist(r + 1, vector<int>(c + 1, 0x3f3f3f3f));
        deq.push_back({0, 0});
        dist[0][0] = 0;
        while (!deq.empty()) {
            auto p = deq.front();
            deq.pop_front();
            int _x = p.first;
            int _y = p.second;

            // 遍历其相邻格点(4个斜方向)
            for (int i = 0; i < 4; i++) {
                int x = _x + book[i][0];
                int y = _y + book[i][1];

                if (x >= 0 && x <= r && y >= 0 && y <= c) { // 防止越界
                    int c = 1; // 默认边权为1

                    // 检查原本的边的方向(看上面的图找个规律就好)
                    if (i == 0 && g[_x][_y] == '\\') { // 反斜杠记得转义
                        c = 0;
                    } else if (i == 1 && g[x][_y] == '/') {
                        c = 0;
                    } else if (i == 2 && g[_x][y] == '/') {
                        c = 0;
                    } else if (i == 3 && g[x][y] == '\\') {
                        c = 0;
                    }

                    if (dist[_x][_y] + c < dist[x][y]) {
                        dist[x][y] = dist[_x][_y] + c;
                        if (c) { // 当前边权非0,放入队尾
                            deq.push_back({x, y});
                        } else { // 当前边权为0,放入队首
                            deq.push_front({x, y});
                        }
                    }
                }
            }
        }

        if (dist[r][c] != 0x3f3f3f3f) { // 可达
            cout << dist[r][c] << "\n";
        } else { // 不可达
            cout << "NO SOLUTION\n";
        }
    }
    return 0;
}

"正是我们每天反复做的事情，最终造就了我们，优秀不是一种行为，而是一种习惯" ---亚里士多德