「线段树」!(简单)的线段树
本题为3月20日23上半学期集训每日一题中B题的题解
题面
题目描述
给你一个序列 \(A[1],A[2],...,A[n]\) .( \(|A[i]| \leq 15007, 1 \leq N \leq 50,000\) ).
M( \(1 \leq M \leq 500,000\) ) 次询问,每次询问 \(Query(x, y) = Max{A[i] + A[i+1] +...+ A[j]; x \leq i \leq j \leq y}\) .
输入
第一行输入一个数N。
第二行输入N个数 \(A[1],A[2],...,A[n]\) .
第三行输入一个数M
以下M行,每行输入x , y.
输出
M行,每行输出查询的答案。
样例输入
3
-1 2 3
1
1 2
样例输出
2
思路分析
本题需要用到名为线段树的高级数据结构,如果你还不会,可以只阅读基础模型部分,掌握此类题运用分治法的解题思路.等日后你学会了线段树之后,再来研究如何进行本题所需要的区间查询.
此题是分治法中非常经典的区间最大连续子段和问题.想要解决这个问题,首先你需要会解决最基础的模型.这个问题最基础的模型,是对于给出的数组,求其整段上的最大连续子段和.对于这个最基础的模型,其实还有另一种更优的动态规划的做法(一种说法是这种方法其实是贪心),但由于此题只能用分治法,所以这里只介绍分治法的做法.关于这个模型的三种做法(还有一种是暴力),可以在《数据结构与算法分析》一书的第2.4.3章中查阅到详细介绍.
基础模型
首先我们来考虑一下,对全段如何求它的最大连续子段和.
显然,最大连续子段和只会出现在全段的三个地方,左半段,右半段,或者是横跨中间.这咋一看是一句废话,但这句废话就是确立此题的分治策略的关键.
如果最大连续子段和出现在左半段,那么也就是说左半段的最大连续子段和就是当前的最大连续子段和,我们只需要求左半段的即可.那如何求左半段呢?显然,此时我们需要解决的问题是一个缩小了规模的相同问题,我可以递归地用分治法去解决.出现在右半段同理.
如果出现在中间呢?所谓出现在中间,就是横跨了左右两端,所以此时的答案一定是左半段的最大后缀和加上右半段的最大前缀和.初读这段话,你可能还没法马上理解.这边简单解释一下:
- 首先,只在一边的情况前面已经处理了,所以横跨中间一定是同时经过两边的情况.
- 其次,既然同时经过两边,还要连续,那一定会包含左半段的最后一个元素和右半段的第一个元素,所以是左半段的后缀和加上右半段的前缀和.
- 最后,左右两段显然是独立的,要想最后两段加起来的和最大,只能让两段都分别最大.

(这里补充一下,如果你做的就是基础模型,那么你还可以采用从中间向两边扩散的方法来求横跨中间情况的和.但是毕竟此处我们最终并不是去做基础模型,这种扩散法是不适合线段树的,所以这里我们不介绍这种做法)
所以我们只需要递归地用分治法求出左半段的最大连续子段和,右半段的最大连续子段和,以及左半段的最大后缀和加上右半段的最大前缀和的和,然后取它们中最大的那个就行了.
但是,如何求左半段的最大前缀和,以及右半段的最大后缀和呢?这里我们一样需要分治地去求.显然,左半段的最大前缀和会有两种情况,一种是其左半段的最大前缀和,另一种是其左半段的和加上其右半段的前缀和(即跨越中间),这里的分析和上面是同理的,可以直接看下面这张图:
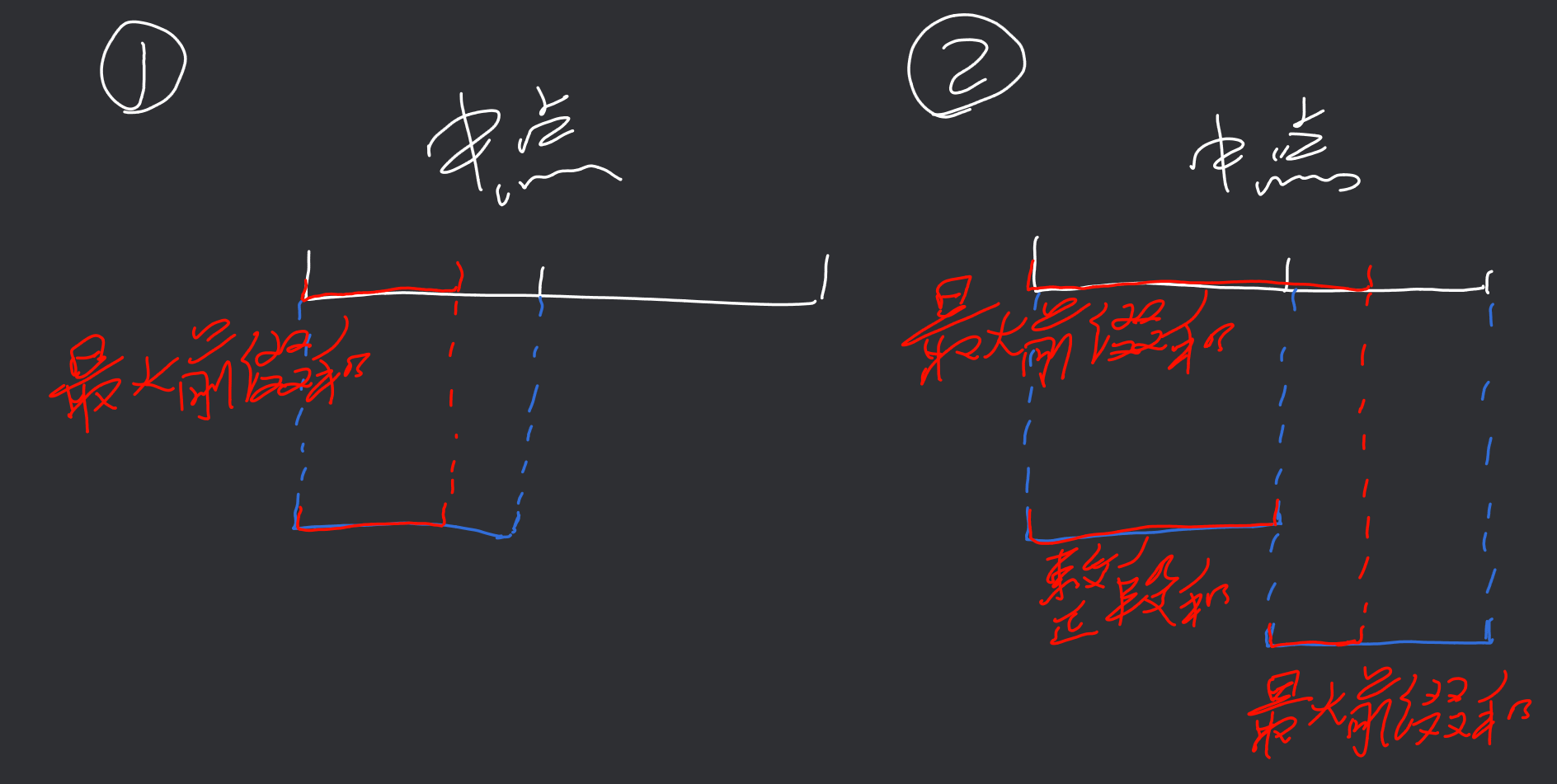
对于右半段是同理的.
所以这个基础模型的解决思路就很清晰了,我们不断地递归当前段的左右半段,分治地去求它们的整段和、最大前缀和、最大后缀和、最大连续子段和,然后按照上面所说的方式,用这些信息去计算当前段的同种信息即可.递归的基线条件就是区间只有一个数,此时上面的这些信息都是这个数本身,直接返回即可.实现起来的代码类似树形dp(实际上树形dp也可以理解成是一种分治法).
可以先尝试在力扣上用上面所说的分治法AC这个基础模型的板子题,然后再继续阅读.注意一下力扣写代码的方式和普通oj不同,它是用类似ACWing上交互题的方式编写代码的,如果你不会在力扣上做题,那还是直接继续读下去吧.
参考代码
这里给出上面所说的板子题的参考代码:
时间复杂度: \(O(NlogN)\)
空间复杂度: \(O(logN)\) (不计入输入数据所用空间,计入递归栈所使用空间)
class Solution
{
public:
int maxSubArray(vector<int> &nums)
{
this->nums = nums;
return solve(0, nums.size() - 1).maxSum;
}
private:
// 输入的数组
vector<int> nums;
// 每一段上维护的信息
struct Node
{
int sum; // 全段和
int lSum; // 最大前缀和
int rSum; // 最大后缀和
int maxSum; // 最大连续字段和
};
// 分治递归函数
Node solve(int l, int r)
{
// 基线条件,当前区间只有一个点,每一个信息都是数组中的这个数,直接返回
if (l == r)
{
return {nums[l], nums[l], nums[l], nums[l]};
}
int mid = l + r >> 1; // 中点
auto left = solve(l, mid); // 分治递归左半段
auto right = solve(mid + 1, r); // 分治递归右半段
// 计算当前段结果
Node res;
res.sum = left.sum + right.sum; // 总和直接加
res.lSum = max(left.sum + right.lSum, left.lSum); // 最大前缀和是左段的最大前缀和,或左段的总和加上右段的最大前缀和
res.rSum = max(left.rSum + right.sum, right.rSum); // 最大后缀和是右段的最大后缀和,或右段的总和加上左段的最大后缀和
res.maxSum = max({left.maxSum, right.maxSum, left.rSum + right.lSum}); // 最大连续子段和,是左段最大连续子段和、右段最大连续子段和,以及左段最大前缀和与右段最大后缀和的和,这三者中的最大值
return res;
}
};
当前问题
解决了基础模型,接下来我们来解决这道题目.此题和基础模型唯一的区别在于,基础模型是求整段的最大连续子段和,而此题是求任意一个区间的最大连续子段和,即,需要实现区间查询.提到区间查询,我们一般都会立刻想到线段树,这个可以看作是分治法具象化所形成的高级数据结构,可以很轻松地解决区间查询.而巧的是,我们前面解决基础模型的思路,正好就是完完全全的分治法,而且此题没有修改(如果有,就是按照线段树正常的修改法),所以我们直接把上面的分治法的思路改成线段树即可.
这里唯一要注意的是查询的时候,如果只有一个子区间,缺少另一个区间,那么显然当前段的各个需要维护的数据就是这个唯一的子区间的相应数据,我们直接把它返回即可.
另外,这道题题目存在问题,实际测试出来此题是多组输入(多组n),但是题目完全没有给出相应的信息.如果你不写多组输入,那么只能通过50%的测试点.
参考代码
时间复杂度: \(O(MlogN)\)
空间复杂度: \(O(N)\)
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
//////线段树开始////////
namespace std {
class SegmentTree {
public:
/*
节点信息
*/
struct Node {
int l, r; // 当前结点区间范围
int sum, lSum, rSum, maxSum; // 维护信息,分别为全段和、最大前缀和、最大后缀和、最大连续字段和
};
/*
原始数组
*/
int *a;
/*
数据长度
*/
int n;
/*
线段树
*/
Node *tr;
/*
初始化线段树
*/
SegmentTree(int n, int *&a) {
this->a = a;
tr = new Node[n + 1 << 2];
build(1, 1, n);
}
/*
析构线段树
*/
~SegmentTree() { delete[] tr; }
/*
更新父节点信息
*/
void pushUp(int u) {
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;// 总和直接加
tr[u].lSum = max(tr[u << 1].lSum, tr[u << 1].sum + tr[u << 1 | 1].lSum);// 最大前缀和是左段的最大前缀和,或左段的总和加上右段的最大前缀和
tr[u].rSum = max(tr[u << 1 | 1].rSum, tr[u << 1 | 1].sum + tr[u << 1].rSum);// 最大后缀和是右段的最大后缀和,或右段的总和加上左段的最大后缀和
tr[u].maxSum = max({tr[u << 1].maxSum, tr[u << 1 | 1].maxSum, tr[u << 1].rSum + tr[u << 1 | 1].lSum});// 最大连续子段和,是左段最大连续子段和、右段最大连续子段和,以及左段最大前缀和与右段最大后缀和的和,这三者中的最大值
}
/*
建树
*/
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) {
tr[u].sum = a[l];
tr[u].lSum = a[l];
tr[u].rSum = a[l];
tr[u].maxSum = a[l];
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushUp(u);
}
/*
查询
*/
Node query(int u, int l, int r) {
// 区间完全包含,直接返回
if (tr[u].l >= l && tr[u].r <= r) {
return tr[u];
}
int mid = tr[u].l + tr[u].r >> 1; // 中点
if (r <= mid) { // 不存在右区间,直接返回左区间
return query(u << 1, l, r);
}
if (l > mid) { // 不存在左区间,直接返回右区间
return query(u << 1 | 1, l, r);
}
Node left = query(u << 1, l, r); // 查询左半段相应信息
Node right = query(u << 1 | 1, l, r); // 查询右半段相应信息
// 计算当前段结果(与pushUp相同,这里不重复注释了,其实也可以改造一下pushUp函数,然后这里也调用它)
Node res;
res.sum = left.sum + right.sum;
res.lSum = max(left.lSum, left.sum + right.lSum);
res.rSum = max(right.rSum, right.sum + left.rSum);
res.maxSum = max({left.maxSum, right.maxSum, left.rSum + right.lSum});
return res;
}
/*
查询调用入口
*/
Node query(int l, int r) { return query(1, l, r); }
};
} // namespace std
//////线段树结束////////
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n;
while (cin >> n) { // 注意题目有误,需要多组输入
int *a = new int[n + 1];
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
SegmentTree st(n, a); // 构建线段树
int m;
cin >> m;
while (m--) {
int x, y;
cin >> x >> y;
if (x > y) { // 以防万一
swap(x, y);
}
cout << st.query(x, y).maxSum << "\n";
}
delete[] a;
}
return 0;
}
"正是我们每天反复做的事情,最终造就了我们,优秀不是一种行为,而是一种习惯" ---亚里士多德
这里是浙江理工大学22届ACM集训队的成员一枚鸭!
本文首发于博客园,作者:星双子,除了我自己的转载请注明原文链接:https://www.cnblogs.com/geministar/p/zstu23_3_20_B.html



