「并查集」改变道路

本题为1月1日22寒假集训每日一题题解

题目来源:(未知)

题面

题目描述

有n个城市和m条道路，每条道路连接两个城市。每条道路都是单向的，但你可以决定每条道路的方向。一个城市如果没有通向它的道路，就被认为是独立的，但允许有从这个城市通往其他城市的道路。请问最小的独立城市的数量。

输入

第一行输入两个数字n,m。表示城市的数量和道路的数量。接下来m行每行两个数字u,v,表示u,v两座城市中有一条道路相连。(2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000).

输出

输出一个数字，表示独立城市的最小数量。

样例输入

【样例输入1】
4 3
2 1
1 3
4 3
【样例输入2】
5 5
2 1
1 3
2 3
2 5
4 3
【样例输入3】
6 5
1 2
2 3
4 5
4 6
5 6

样例输出

【样例输出1】
1
【样例输出2】
0
【样例输出3】
1

---

思路分析

本题需要较多的思考,对思维要求比较大,希望各位阅读时多多思考.

本题咋一看难以入手,甚至毫无头绪.为了找到思路,所以我们从最简单的情况入手来看,逐步分析.

本题所形成的结构显然是图,而最简单的图显然是,所有点成线性的情况.对于这种情况,想要使得最终独立的点最少,显然只需要每条边向着同一个方向即可.此时只有位于开头的点是独立点,且显然我们无法产生0个独立点的情况,故此情况确实取得最少独立点.

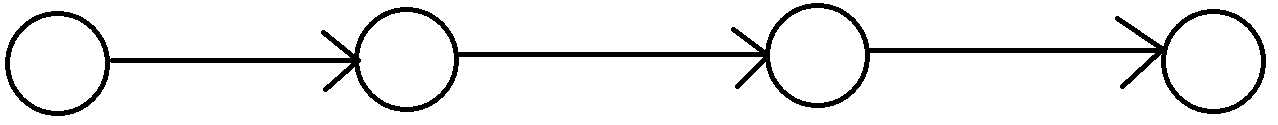
接下来是形成树的情况.树也有很多情况,所以我们从最简单的情况分心.首先,显然,对于一颗倒V形的树,其实就是把线性表中间的某个节点折了过来,此时与线性表的情况是一致的,其中一个叶子节点作为开头的独立点,每条边指向一个其他节点即可.

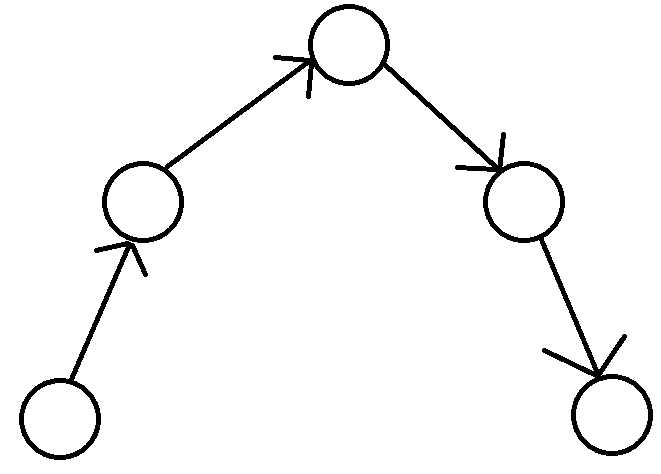
那如果是倒W形的树呢?此时可以看成是将一条线性表接在了另一个线性表的中间某个节点上,然后把这个节点折了过来,所以此时与线性表依然是一致的,其中一个叶子节点作为开头的独立点,每条边指向一个其他节点即可.

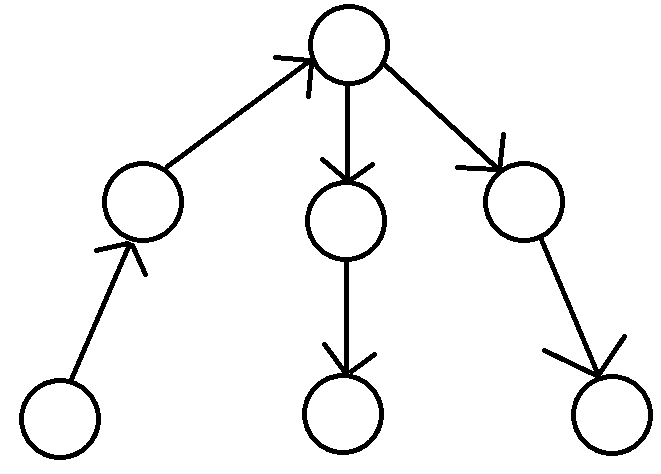
用同样的理解方法,对于一颗任意的树,我们都可以看成若干线性表的组合,那么同样,只需要一个叶子结点作为开头的独立点,每条边指向一个其他节点,即可取得最小独立点数的情况.

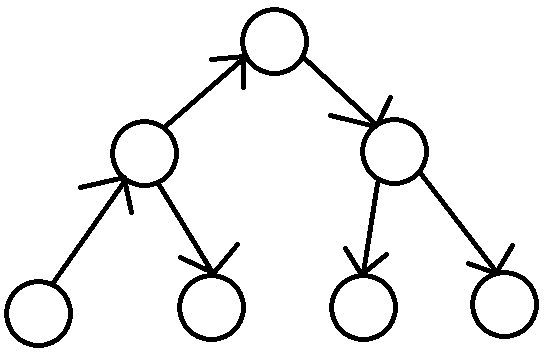
当然,如果认真观察,我们会发现此时我们又另外一种指定边方向的方案,即将根节点的入度看成0,其他边均指向子节点,此时同样只有一个独立点(根节点).其实再仔细观察我们也可以发现,此规律和前面线性表得出的规律也是符合的(我们可以把线性表的第一个节点看成根节点).为了后续叙述方便,此处我们采用这种规律,而不是上面把叶子结点作为独立点的规律.

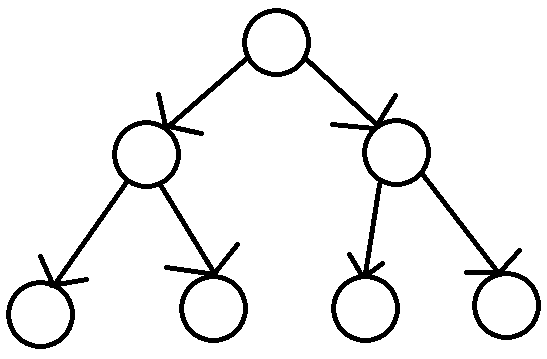
接着就是图的情况了.在连通(不是强连通,下同)的无环图中,显然可以和树一样去理解,找出合适的根节点,将其作为独立点即可.此时最小的独立点数依旧是1,且显然无法取得0个独立点的情况.

但是对于连通的有环图来说,上面的规律就不适用了,不过好在我们可以近似去理解.我们可以把环中的一个点看成"根节点",由于存在环,此时我们只需要将形成环的那条边调转方向,指向这个"根节点",即可使得这个根节点不再独立,此时整个图上不会存在任何一个独立点(可以看成,加上这条形成环的边前,此图只有"根节点"是独立点;在加上这条边后,由于其方向指向"根节点",所以"根节点"不再独立),此时最小独立点数为0.

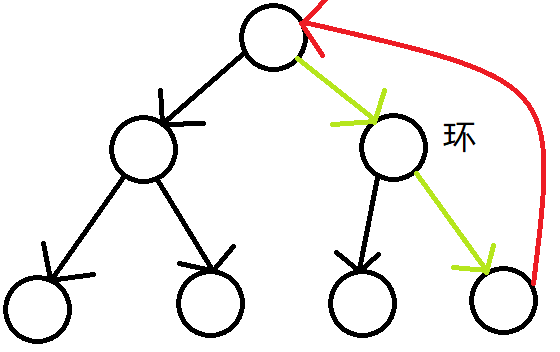
综上,我们成功分析了连通图可能出现的所有情况,总结起来就是,无环最小独立点数为1,有环为0.

那么对于不连通的图呢?显然,可以当成多个子图来处理,每一个无环子图能产生一个最小独立点数,每个有环子图能产生0个最小独立点数.所以,我们只需要统计所有子图中的无环图即可.

到此这道题的思路就有了,我们只需要根据输入进来的数据,判断有多少个子图是无环图即可.无环子图的数目就是最终要求的最小独立点数.我们有多种方法取得答案,这里数据量比较大,且由于只需要看连通性和有无环,所以我使用了时间复杂度接近常数(实际为阿克曼函数的反函数)的并查集来处理.当然也有其他做法,比如直接用深度优先搜索,这样也可以找出有几个无环的子图,不过时间复杂度劣于并查集的做法,感兴趣可以自行研究(很好写).

并查集可以动态维护出每个连通块,利用它即可得到当前图子图的数量.而当将加入新的一条边时,如果并查集中已经记录这条边所连接的两个点属于同一个连通块,那么这条边的加入就会使得这幅子图中形成环.所以我们只需要动态维护一个计数器,初始值为这个图中点的个数(在连接所有边之前,一个n个顶点的图可以看成是由n个子图组成的图,每个子图就是一个点),在动态连接每条边时,如果两个图合并,其中一个为无环图,计数器自减;如果一个图成为了有环图,计数器自减.这样即可在所有点输入之后直接取得我们所需要的答案.

参考代码

由于存在并查集,此题的代码较长,这里为了阅读方便,将并查集和核心代码拆开成两部分

并查集部分(使用面向对象的编程思想,此处代码似乎存在bug,但是交上去是AC的):

namespace std
{
    /*
        简易并查集
        使用不可变数组实现,各元素编号从0开始
        为方便扩展,对外开放内部使用的两个数组

        此题中为了实现算法,增加了记录每个连通块是否有环的数组和记录独立城市数量变量两个属性

        @author 星·双子
        @version 1.0
        @date 2022/10/29
    */
    class UnionFindSets
    {
    private:
    public:
        /*
            模拟链表
        */
        int *par;
        /*
            记录每个连通部分路径压缩前树的深度
        */
        int *rank;
        /*
            此题额外部分,记录每个连通块是否有环
        */
        bool *isLoop;
        /*
            此题额外部分,记录独立城市数量(独立城市即为无环的每组的一个叶子节点)
        */
        int count;

        UnionFindSets(int);
        ~UnionFindSets();
        int find(int);
        void unite(int, int);
        bool same(int, int);

        int operator[](int);
    };

    /*
        查询指定元素的根节点

        均摊时间复杂度O(α(n))

        @param x{int} 指定的元素编号
        @return {int} 根节点元素编号
    */
    int UnionFindSets::find(int x)
    {
        if (par[x] == x) // 基线条件,本身就是根节点,直接返回
            return x;

        // 不断向上递归地搜索根节点,同时进行路径压缩,将当前结点的父节点直接改成根节点
        return par[x] = find(par[x]);
    }

    /*
        将[]重载为find函数,通过[]运算符即可获取根节点
        但不支持通过此方式来连通两个连通部分

        @return {int} 根节点元素编号
    */
    int UnionFindSets::operator[](int x)
    {
        return find(x);
    }

    /*
        连通两个连通部分

        均摊时间复杂度O(α(n))

        @param x{int} 第一个连通部分中的任意一个元素编号
        @param x{int} 第二个连通部分中的任意一个元素编号
    */
    void UnionFindSets::unite(int x, int y)
    {
        // 分别找到两个连通部分的根节点
        x = find(x);
        y = find(y);

        // 如果本来就连通,再次进行连通即会成为环
        if (x == y)
        {
            // 如果之前没有成环,由于可以将环中的一个点看成新的顶点,并令其两边一进一出来消除一个独立点,所以需要把独立点数量减一
            if (!isLoop[x])
            {
                count--;
                isLoop[x] = true; // 标记此连通块存在环
            }

            return;
        }

        // 将深度小的连通部分接在大的上
        if (rank[x] < rank[y])
        {
            // 如果之前没有成环,由于少了一个顶点(被合并进了新的连通块),相当于少了一个独立点,把计数器减一
            if (!isLoop[x])
            {
                count--;
            }
            isLoop[x] |= isLoop[y]; // 同步连通状态

            par[x] = y;
        }
        else
        {
            // 如果之前没有成环,由于少了一个顶点(被合并进了新的连通块),相当于少了一个独立点,把计数器减一
            if (!isLoop[y])
            {
                count--;
            }
            isLoop[y] |= isLoop[x];// 同步连通状态

            par[y] = x;
            // 如果两个连通部分深度一样,此时连通后深度会加一
            if (rank[x] == rank[y])
            {
                rank[x]++; // 只需要操作根节点就好了
            }
        }
    }

    /*
        判断两个元素是否连通

        @param x{int} 元素1
        @param x{int} 元素2
        @return {bool} 是否连通
    */
    bool UnionFindSets::same(int x, int y)
    {
        // 判断根节点是否相同即可
        return find(x) == find(y);
    }

    /*
        构造函数
        初始化相关数组

        时间复杂度O(n)

        @param {int} 总结点数
    */
    UnionFindSets::UnionFindSets(int n)
    {
        par = new int[n];
        rank = new int[n];
        isLoop = new bool[n];
        count = n;
        for (int i = 0; i < n; i++)
        {
            par[i] = i;
            rank[i] = 0;
            isLoop[i] = false;
        }
    }

    /*
        析构函数
        释放相关内存空间
    */
    UnionFindSets::~UnionFindSets()
    {
        delete par;
        par = nullptr;
        delete rank;
        rank = nullptr;
    }
}

核心代码部分:

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <iostream>

using namespace std;

int main()
{
    ios::sync_with_stdio(false);

    int n, m;
    cin >> n >> m;
    UnionFindSets ufs(n); // 并查集对象

    while (m--)
    {
        int u, v;
        cin >> u >> v;
        u--; // 将编号转为从1开始
        v--; // 将编号转为从1开始

        ufs.unite(u, v); // 将两个节点连通
    }

    cout << ufs.count << "\n"; // 直接获取并查集中计算出的独立点数量即可,由于n额外加了1,所以这里需要把1减回来

    return 0;
}

"正是我们每天反复做的事情，最终造就了我们，优秀不是一种行为，而是一种习惯" ---亚里士多德