「组合数学」隔离区
本题是组合数学中的卡特兰数问题,此处给出了用分治思想推出卡特兰数递推公式的分析思路.
题目来源:(未知)
我们先来看一下这题的题面.
题面
题目描述
西安发生新冠疫情了。不少人进了隔离区。
隔离区是一个凸多边形,为了隔离人员的安全,我们需要用木板将隔离区分隔开。为了隔板的稳定,隔板两边分别与凸多边形的顶点相接,当然隔板不能被其他隔板断开。
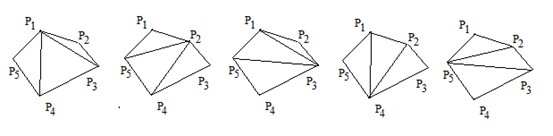
凸多边形是5的情况,有上面5种划分方案。
现在知道顶点个数,你知道有多少种隔离方案,使得每个区域是三角形?
输入
一个整数n (3<=n<=20)
输出
一个整数,即方案数
样例输入
5
样例输出
5
题目分析与常见错误思路
显然,这是一道卡特兰数的问题,如果你知道什么是卡特兰数,那么直接带卡特兰数的递推公式即可解决该问题.
那如果我不知道什么是卡特兰数,或者没想到这题是卡特兰数的问题,又如何解决呢?别急,我们慢慢分析.
就先从n=3的情况开始分析吧.首先很显然,n=3的多边形就是三角形,而对于一个三角形,它划分成三角形的方案数就是1,因为它本身就已经是一个三角形了,无需划分.
那么n=4呢?这个时候的图形是个四边形,简单分析可以知道,沿着两条对角线分别可以把它分成两个三角形,所以这时的划分方案就是2,如下图:
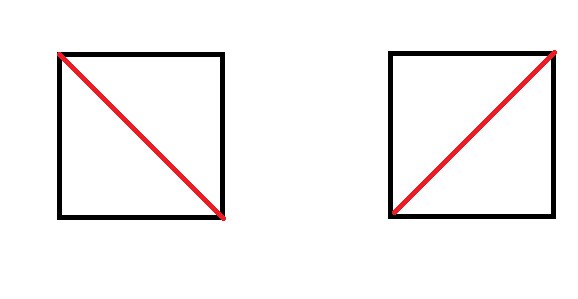
那么n=5呢?好像这次没有之前那么直观了,不过好在这种情况题面上已经直接给出了:

相信有不少同学经过对上图的仔细观察,再加上自己对多边形划分的理解,发现5边形的划分方式就是分别选择5个顶点中的一个,然后向不相邻的顶点连线,所以是5种方案.于是他们由此认为,n边形的划分方案也是遵循这个规律的.(你还别说,我第一次做类似的题目的时候,我也是这么想的).
实际上,如果把这种思路提交上去,得到的结果只会是WA.

今天又是陪伴WA的一天呢
其实,我们只要继续对6边形的划分稍加分析,就会找到上述思路的规律的反例,比如下图这种6边形的划分法,显然是不满足这个规律的:
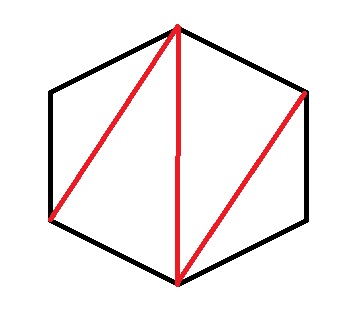
正确思路
那正确的规律是什么捏?别急,我们先回到5边形的划分中,我们仔细找找有什么潜在的规律.
显然,对于每种划分情况,总会存在一个三角形,它总有至少一边是在原本的五边形上的,而且这个规律是可以推广到n边形的.(不信?如果没有三角形的边在n边形上,那是不是所有三角形都跑到图形里面去啦?这样就不是在进行三角形划分了鸭!严格的数学证明这里就略了 才不是我不会证)
所以,我们可以在这个五边形的5条边中任意选择1条边作为划分出来的那个三角形的一条边.由于我们只看划分的方案,边的长度是无关紧要的,所以这个五边形旋转72°(360°/5)后和原本的图形可以看成和原本的图形是同一个图形(对n边形自然也成立,因为只需要划分方案数,显然这与这个凸n边形长啥样无关,所以可以直接把这个n边形直接看成是正n边形),因此,无论我们选哪条边,本质上都是选了同一条边,所以这里随便选1条来分析即可.
现在有了一条边了,距离组成三角形还差一个点.所以我们在剩下来的3个点中可以任意选择一个点,根据分类加法原理,只需要把选择每个点的情况所算出来的方案数都加起来,就是最终的答案了.
我们先来看取如下点的情况:
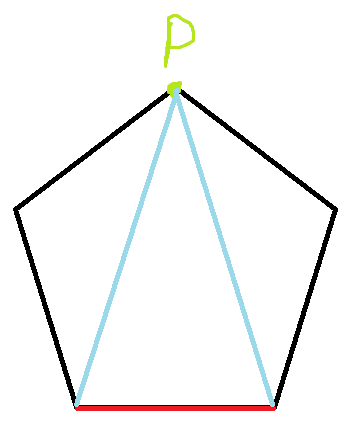
此时三角形选择完毕后,剩下的左右两边是两个三角形,显然已经完成了划分.
接下来看取另一个点的情况:
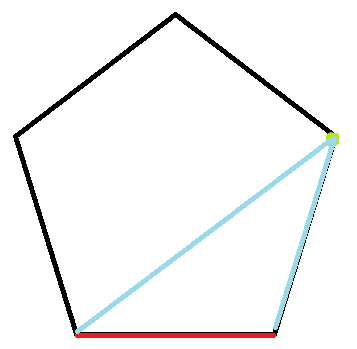
此时三角形选择完毕后,剩下的右边已经没有图形了,而左边是一个四边形.诶,怎么是四边形,四边形怎么办呢?
别急,我问你,如果我直接给你一个四边形,我要你划分成三角形,你会划分吗?显然是可以直接完成的,前面也已经讨论过了,是两种划分方式.
而在这里,是不是也是同样的?我们只需要对这个四边形继续求划分方案,是不是就可以啦?也就是,在这里,我们通过选一条边和一个点划分出一个三角形,来将问题的规模从原本的5降低到了4.
还有一个点的选取情况与上面类似,最后也是两种划分方式,这里就略过了.根据上述分析,我们可以成功求得5边形的划分方式是5.
我们再来看看在六边形中能否做到同样的事情,我们先选择这一个点来分解:
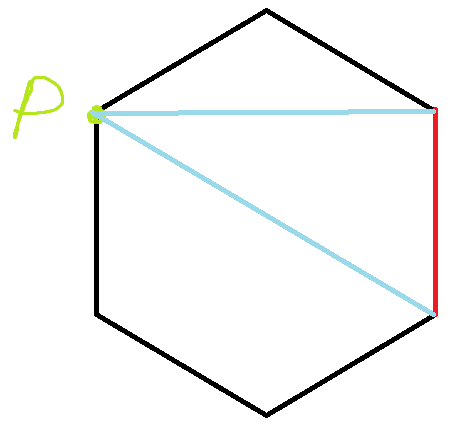
此时上面是一个三角形,下面是一个四边形,我们确实也成功地把问题分小了.接下来只要对下面的四边形计算有几种划分方案即可,上面已经讨论过了两次了,这里不多赘述了.
那如果我们选择这一个点呢?
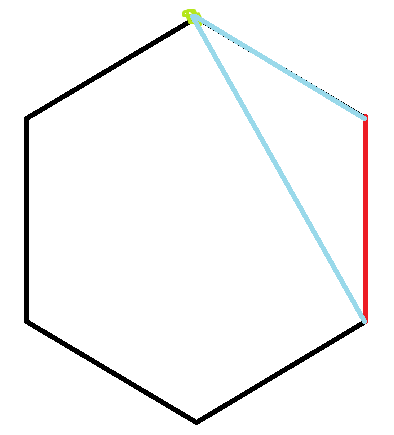
显然,此时问题也一样变小了,上面已经没有图形了,而下面是一个5边形.啊咧,5边形怎么办捏?别急,前面规模降低到4边形的时候,是不是接着对4边形进行划分鸭?那这里我们自然可以一样地对这个5边形继续划分,怎么划分捏?前面不是刚刚分析过五边形的划分方法嘛.我们可以接着选一条边,然后通过选点继续降低规模求解.
分析到这里,此题的思路基本已经有了.我们先固定n边形的一条边,然后依次选择剩下的各个点,这样划分后剩下的图形的边数就会变小,然后对每一个分小后的部分进行同样的操作,即继续进行固定边、选点来分小,直到问题规模变成可以直接求解的3边形或4边形.根据分步乘法原理,此时只需要把划分出来的左右两个多边形的划分方法数相乘,就是当前选择的这个点的划分方法数啦!然后再根据分类加法原理,把每个点的划分方法数加起来,就是最后的答案啦!
不过这里有个小小的问题,前面的分析中有出现过选择一个点后,一边已经没有图形的情况.为了和上面统一,我们希望这种情况也可以使用分步乘法原理.为此,我们人为规定此时的划分方法数为1(此时可以看成"2边形",所以也就是人为规定"2边形"的划分方法数是1),这样就没有问题啦!
上述这种思路是一种叫做分而治之(divide and conquer),即分治思想的应用.我们将大规模问题不断分解成小规模问题,即减小问题的规模,然后再对每一个小规模问题进行同样的操作,分成更小规模的问题,即进一步减小问题的规模,如此下去,直到问题被分成小到可以直接解决的规模为止.然后我们便可从这些已经解决的小问题逐步推回,最终解决大问题.快速排序就是典型的分治思想的例子,通过对数组中的每一段进行小放左、大放右的排序,最终完成对整个数组的排序.此外二分搜索等也是分治思想的典型例子.
Nothing is particularly hard if you divide it into small jobs.
如果你能把要做的事情化整为零,就没有什么事会特别困难。
——Henry Ford(亨利·福特)
代码编写
好了,思路找到了,接下来就来写代码吧!
在分治思想中,我们对每个划分出来的小问题执行的操作和对原本的大问题执行的操作是一样的,这非常符合递归的特点,所以我们可以用递归来解决此问题.
我们先写一个函数,用来计算划分数目,局部参考代码如下:
int f(int n)
{
}
显然,递归的基线条件就是3边形和"2边形"的情况(4边形可以通过3边形和"2边形"算出来,所以无需列入基线条件.当然,如果你想这么干也可以),此时无需继续递归,可以直接返回值,局部参考代码如下:
// 基线条件,3边形只有一种划分方式,"2边形"为了统一,人为规定有一种划分方式,此时可以直接返回,结束递归,开始逐步返回值计算结果
if(n == 3 || n == 2)
{
return 1;
}
接下来就是分治的核心代码了,由于有多种分法,所以我们需要写一个循环来分别计算每一种分法的结果数目,然后求和,这个和即为结果.
那这个循环怎么写呢?我们观察一下从最近的点开始选点时的规律:
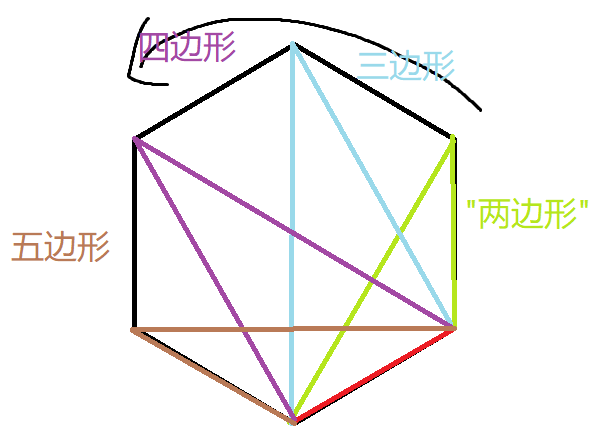
我们可以发现,右侧的多边形从"2边形"一直变化到n-1边形,而左侧的多边形从n-1边形一直变化到"2边形",所以我们可以写一个for循环,将一侧多边形的边数作为循环变量即可.
局部参考代码如下:
int res = 0; // 累加器
for(int i = 2;i < n;i++) // 选点,从最近开始选,一侧会从"2边形"逐步变成n - 1边形
{
// 此处应写 res += 当前情况的结果数目
}
return res;
那如何计算结果数目捏?如前所述,我们使用分治思想,对划分出来的两个部分继续进行同样的操作,即进行递归.然后根据分步乘法计数原理,乘起来就是这种情况的结果数目.
这里可能有些朋友对一侧边数为i时另一侧的边数怎么求感到困惑.当一侧是i边形时,它会用掉多边形的i - 1条边(去掉的那1条是中间的那个三角形上的).此时再去掉中间三角形用掉的多边形上的那1条边,还剩n - (i - 1) - 1,也就是n - i条边.再加上中间三角形上的1条边,那么另一侧的多边形就是n - i + 1条边啦!
如果还是看不出来,也可以直接利用临界条件找规律,然后用数学归纳法简单证明下即可.
局部参考代码如下:
res += f(i) * f(n - i + 1); // 对两个部分进行同样的操作,不断把问题分小,直到可以解决
其实,此时我们推出来的这个式子就是卡特兰数的一种递推公式,但我们在这里并没有运用任何和卡特兰数有关的知识,就已经直接推导出这个递推公式了,怎么样,思维的力量是不是非常强大?
这样这个问题就解决了,这个函数的完整参考代码如下:
int f(int n)
{
// 基线条件,3边形只有一种划分方式,"2边形"为了统一,人为规定有一种划分方式,此时可以直接返回,结束递归
if (n == 3 || n == 2)
{
return 1;
}
int res = 0; // 累加器
for (int i = 2; i < n; i++) // 选点,从最近开始选,一侧会从"2边形"逐步变成n - 1边形
{
res += f(i) * f(n - i + 1); // 对两个部分进行同样的操作,不断把问题分小
}
return res;
}
注:这个题目到这里就已经解决了,下述内容是对上面写的算法进行一些运行时间上的优化.如果你此前没有接触过算法,那么下述这些内容可能会较难理解,可以尝试阅读一下,如果实在看不明白可以不去管它.我还有一篇关于斐波那契数列的博客(目前还没写好,咕咕咕)详细介绍了下面两种优化的思路到底是怎么一回事情,如果感兴趣可以(在发布之后)去看一下.
剪枝
由于目前oj的提交通道已经关闭,我不清楚上述的代码是否会导致TLE(时间超限),但是显然(如果你显不出来也没关系,接着看就好了),上述的代码实际的运行效率会很慢.因为当我们求f(n)的时候,我们求遍了f(2)到f(n-1),而当我们求f(n-1)的时候,我们再次求遍了f(2)到f(n-2),这里有数量非常可怕的重复运算,这并不符合递归的合成效益法则(compound interset rule),我们不应该在不同的递归调用中做重复性的运算.
那怎么优化捏?和对求斐波那契数列中出现的重复计算的处理方法一样,我们也可以通过记忆化搜索的方式来优化掉重复的计算(这种操作称为对递归树进行剪枝).我们引入一个数组,当我们计算出f(i)(2<=i<=n)的时候,我们就把它存在数组下标为i的位置上.当我们下一次用到这个f(i)时,我们就直接从数组中将它取出,不用再继续递归下去算了.这样的一步简单的优化可以大大提高算法的效率.
参考代码如下:
int dp[21]; // 下标0-20,其中0,1,2,3其实是不存数据的.
int f(int n)
{
// 基线条件,3边形只有一种划分方式,"2边形"为了统一,人为规定有一种划分方式,此时可以直接返回,结束递归
if (n == 3 || n == 2)
{
return 1;
}
if (dp[n] != 0) // 当前项已经计算过,直接从数组中取出,不再继续递归
{
return dp[n];
}
// 此时直接把dp[n]当做累加器即可
for (int i = 2; i < n; i++) // 选点,从最近开始选,一侧会从"2边形"逐步变成n - 1边形
{
dp[n] += f(i) * f(n - i + 1); // 对两个部分进行同样的操作,不断把问题分小
}
return dp[n];
}
当然,这里数据量比较小,如果数据量大起来,还要注意一下是否会出现爆int的问题,必要时将相关数据改成long long.
动态规划
和斐波那契数列一样,此处我们还可以进一步优化,将递归改为递推,即改为动态规划.
由于篇幅已经比较长了,并且动态规划并不是本篇所要讨论的主题,所以这里直接给出参考代码,供感兴趣的朋友研究:
#include <stdio.h>
int dp[21];
int main()
{
int n;
scanf("%d", &n);
dp[2] = 1, dp[3] = 1; // 初始状态定义
// 状态转移
for (int i = 4; i <= n; i++) // 从4边形开始递推,直到n边形
{
for (int k = 2; k < i; k++) // 此循环同递归写法
{
dp[i] += dp[k] * dp[i - k + 1];
}
}
printf("%d", dp[n]);
return 0;
}
参考代码
下面给出我自己做这道题时候的完整代码(做的时候记忆化搜索直接过了,就没有为难自己去写动态规划了):
#include <stdio.h>
int dp[21]; // 0-20,其中0,1是不存数据的.
int f(int n)
{
// 基线条件,3边形只有一种划分方式,"2边形"为了统一人为规定有一种划分方式,此时可以直接返回,结束递归
if (n == 3 || n == 2)
{
return 1;
}
if (dp[n] != 0) // 当前项已经计算过,直接从数组中取出,不再继续递归
{
return dp[n];
}
// 此时直接把dp[n]当做累加器即可
for (int i = 2; i < n; i++) // 选点,从最近开始选,一侧会从"2边形"逐步变成n - 1边形
{
dp[n] += f(i) * f(n - i + 1); // 对两个部分进行同样的操作,不断把问题分小
}
return dp[n];
}
int main()
{
int n;
scanf("%d", &n);
printf("%d\n", f(n));
}
提高
就如开头所说的那样,此题其实是一道卡特兰数的问题.在xcpc劝退树中,卡特兰数被归入基础中(同样被归入基础里的还有贪心、二分等基础算法),所以对于acmer来说,卡特兰数还是要好好掌握的.
关于卡特兰数的介绍,这里直接引用维基百科:
卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡特兰命名。历史上,清朝数学家明安图在其《割圜密率捷法》中最先发明这种计数方式,远远早于卡塔兰。
卡塔兰数的一般项公式为:
此外,还具有如下两种递推公式:
组合数学中有非常多的组合结构可以用卡塔兰数来计数.比如合法括号组合 二叉树构成方案 不越过对角线的单调路径 凸多边形划分三角形 进出栈的置换 不交叉划分 填充阶梯状图形 标准杨氏矩阵数量等.
本题就属于凸多边形划分三角形的典型问题.
关于卡特兰数在其他问题上的具体应用,可以查看集训队的一位大佬整理的博客.
"正是我们每天反复做的事情,最终造就了我们,优秀不是一种行为,而是一种习惯" ---亚里士多德
这里是浙江理工大学22届ACM集训队的成员一枚鸭!
本文首发于博客园,作者:星双子,除了我自己的转载请注明原文链接:https://www.cnblogs.com/geministar/p/Isolation_zone.html


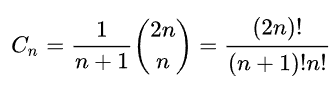
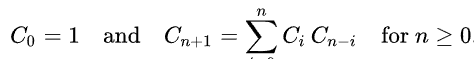
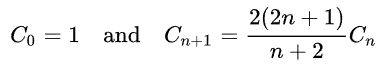

 浙公网安备 33010602011771号
浙公网安备 33010602011771号